一.首先先安装numpy

windows+r 输入cmd

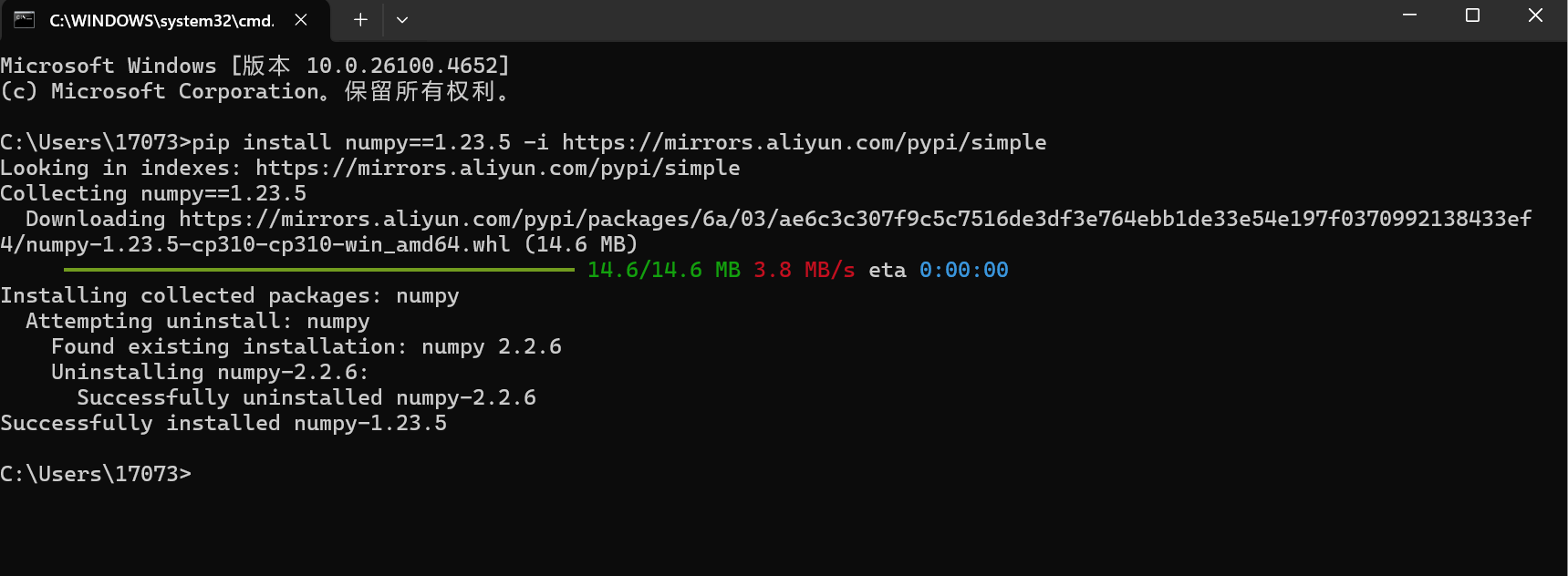
然后像我这样输入进去，加一句后面的https：.....可以放其他他的镜像地址比如

• 清华大学镜像源：Simple Index
• 阿里云镜像源：Simple Index
• 中国科学技术大学镜像源：Verifying - USTC Mirrors
• 豆瓣镜像源：https://pypi.douban.com/simple
• 华为云镜像源：https://repo.huaweicloud.com/repository/pypi/simple
• 腾讯云镜像源：Simple Index
• 网易镜像源：https://mirrors.163.com/pypi/simple

都可以试试

这里可以看看版本

二.概念分析

在编程语境中，array（数组） 是一种基本的数据结构，用于存储和组织相同类型的元素集合。它在不同的编程语言中有不同的实现和特性。以下是关于 array 的详细解释：

1. 通用概念

数组是一个有序的数据集合，每个元素可以通过索引（位置编号）快速访问。数组的特点包括：

• 固定长度：多数语言中，数组创建后长度不可变（如 Java、C++）。
• 相同数据类型：数组中的元素必须是同一种类型（如整数、浮点数）。
• 连续内存：元素在内存中连续存储，便于快速访问。

2. 在不同编程语言中的实现

Python

在 Python 中，原生的数组功能由 list 提供（动态数组），但更常用的是 NumPy 数组（高效的多维数组）：

# Python 列表（动态数组）
my_list = [1, 2, 3, 4]  # 可存储不同类型元素# NumPy 数组（需导入库）
import numpy as np
my_array = np.array([1, 2, 3, 4])  # 元素类型必须一致

NumPy 数组的优势：

• 高效的数学运算（比 Python 列表快得多）。
• 支持多维数组（矩阵、张量）。
• 丰富的科学计算函数。

 3. 数组操作示例

import numpy as np# 创建一维数组
a = np.array([1, 2, 3])# 创建二维数组（矩阵）
b = np.array([[1, 2, 3], [4, 5, 6]])# 访问元素
print(a[0])  # 输出: 1
print(b[1, 2])  # 输出: 6（第2行第3列）# 数组运算
c = a + 2  # 所有元素加2：[3, 4, 5]
d = a * b  # 对应元素相乘

4. 为什么使用数组？

• 高效访问：通过索引直接访问元素，时间复杂度为 O (1)。
• 内存优化：连续存储节省空间。
• 适合数学运算：尤其在科学计算、机器学习中广泛使用。

5. 常见问题

• 索引越界：访问不存在的索引位置（如 a[10]）会报错。
• 类型限制：NumPy 数组要求元素类型一致，否则会自动转换（如 [1, 2.5] → 全浮点数）。

import numpy as np  # 导入numpy库，别名为np，用于高效数值计算等操作
# numpy(底层用C实现，结合Python接口)：在处理数字、矩阵等数据时速度较快，是科学计算库，包含很多数学相关公式# 计算正弦值，参数为弧度，角度（D）和弧度（R）关系：D = (180/π) × R
print(np.sin(1))  
# 计算余弦值（这里补充完整调用，假设计算弧度为1的余弦，可按需修改参数）
print(np.cos(1))  
# 计算正切值（这里补充完整调用，假设计算弧度为1的正切，可按需修改参数，注意正切存在取值限制，部分输入可能出问题）
print(np.tan(1))  
# 计算绝对值
print(np.abs(-1))  

 np.后面就会有很多的数学要用的概念，像这样

 

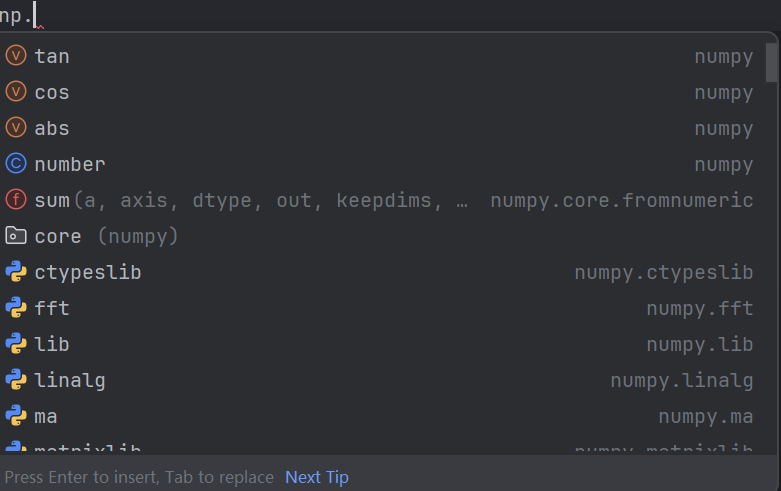
通常包括三角函数反三角函数等

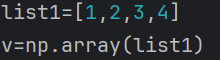
1. 先用 list1 = [6] ，借助 Python 内置的 list（列表）类型，创建一个包含数字 6 的列表 。
2. 再通过 v = np.array(list1) ，调用 NumPy 库的 array 函数，把刚才创建的列表 list1 转换成 NumPy 数组（可理解为用于数值计算的 “矩阵” ），转换后的结果存储在变量 v 里 。

调试后为：

 

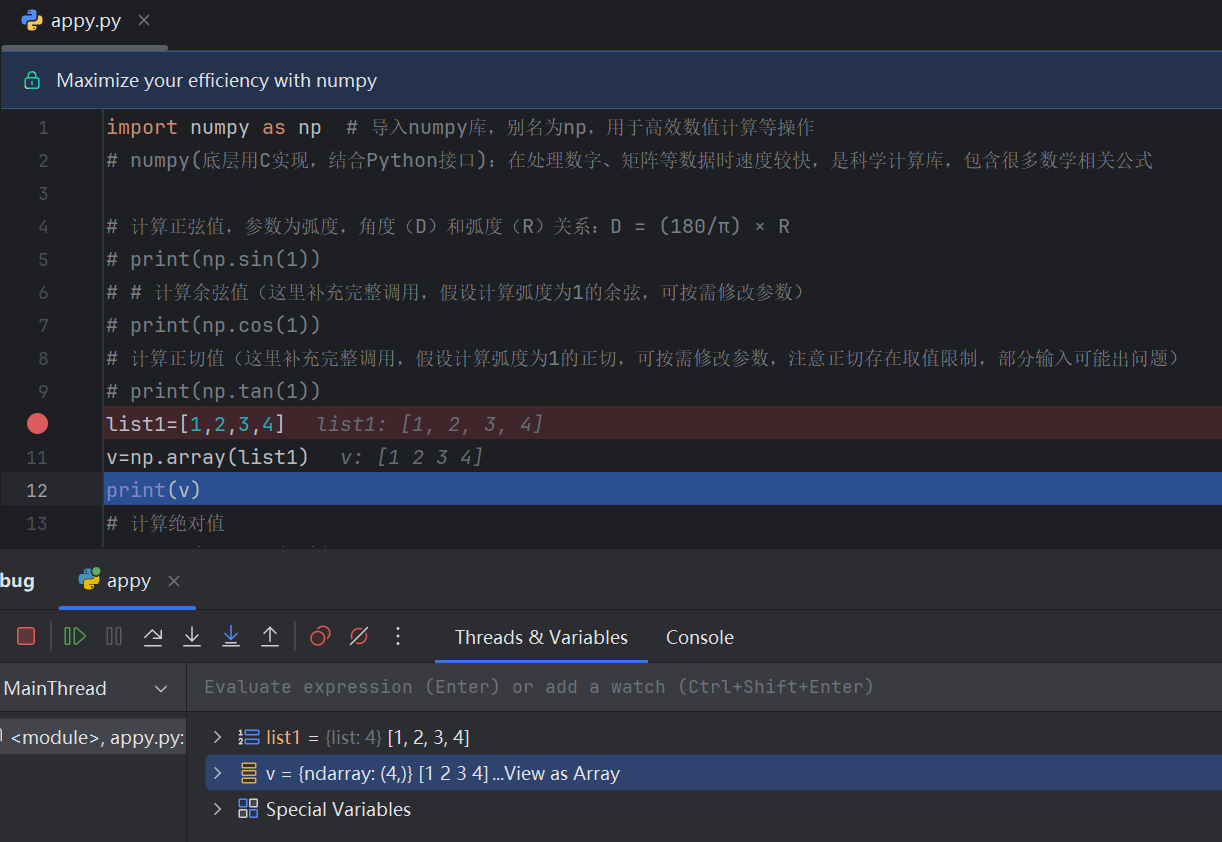
 所以需要记住的是：矩阵的数据类型就是ndarray

v那行有个View as Array点开看看，像这样

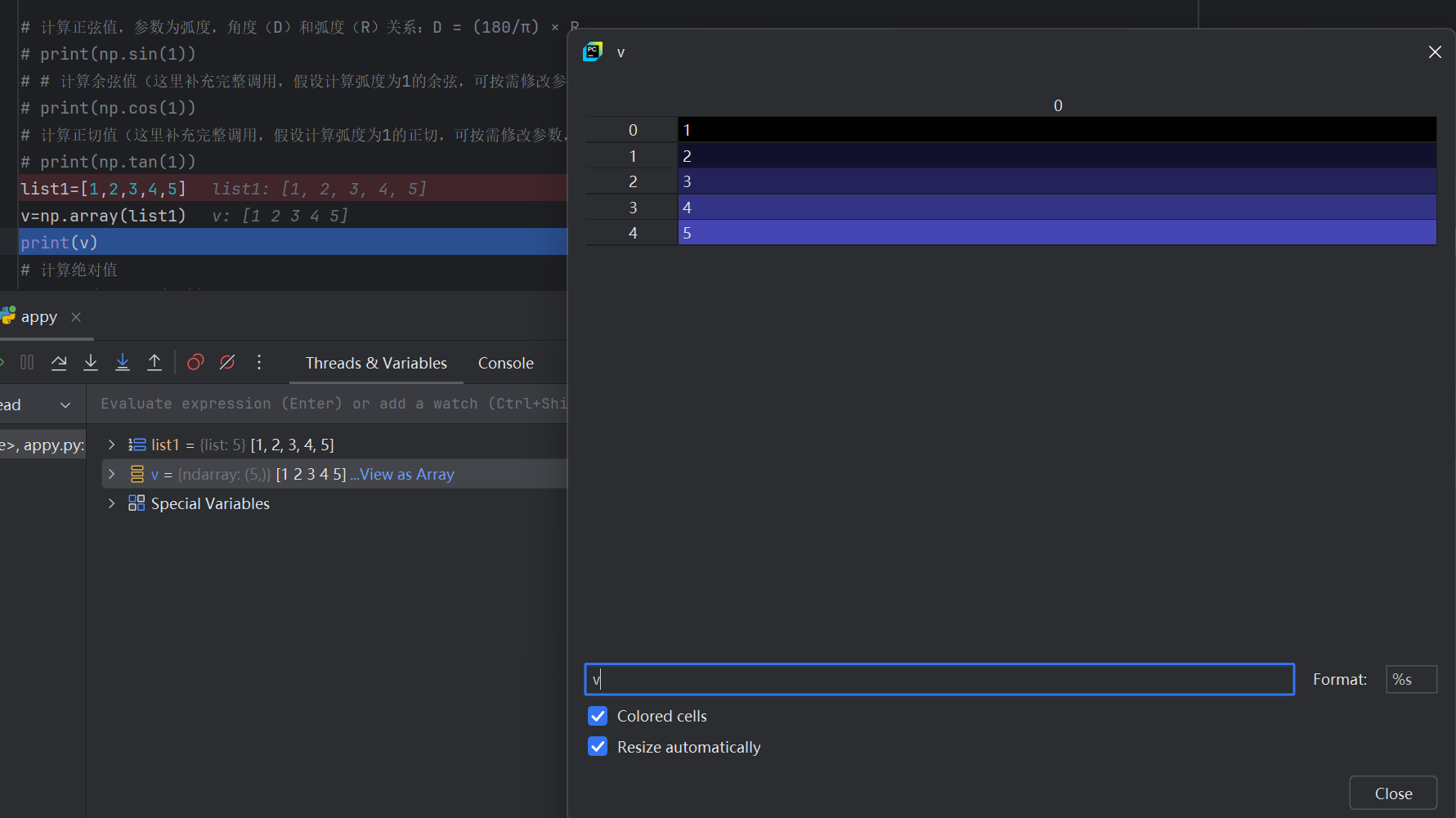
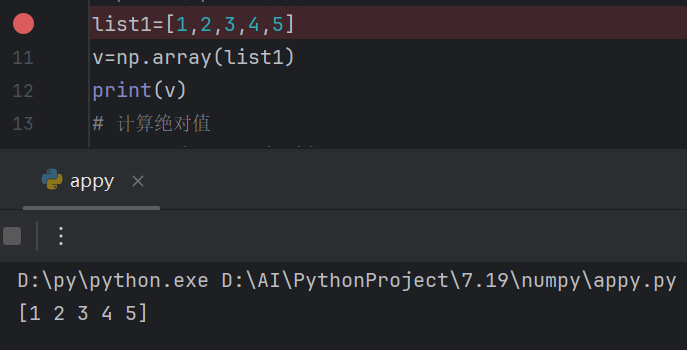
打印的规则和数学一样，矩阵无逗号的，而列表是有逗号的