螺旋矩阵题型总结。我刷了几道螺旋矩阵相关的题目，这里我们介绍一下一些常见的解法。

螺旋矩阵

方形矩阵

当我们遇到n*n的方形矩阵时，可以用一种特殊的解法来遍历实现，以下面这道题为例：

59. 螺旋矩阵 II

我们可以定义几个变量用来控制遍历的行为：

• startX：每次循环的起点的行数

• startY：每次循环的起点的列数

• offset：每循环一圈，用偏移量表现

vector<vector<int>> generateMatrix(int n) {vector<vector<int>> ans(n,vector<int>(n,0));int offset = 1 , startX = 0 , startY = 0;int val = 1;int i,j;for(int k=0;k<n/2;k++){     //循环次数就是圈数for(j=startY;j<n-offset;j++)    //左上->右上（从此以下都是左闭右开）ans[startX][j] = val++;for(i=startX;i<n-offset;i++)    //右上->右下ans[i][j] = val++;for(;j>startY;j--)              //右下->左下    ans[i][j] = val++;for(;i>startX;i--)              //左下->右上ans[i][j] = val++;startX++;startY++;offset++;   //实际上更新offset就是在更新每次循环的边界（缩小）}if (n&1){   //如果矩阵的边长为奇数，最中间的值会没法遍历到ans[offset-1][offset-1] = val;}return ans;}
};

同时还可以将方形矩阵视作一种特殊的矩形矩阵，以下对矩形矩阵的所有解法对方形都适用。

矩形矩阵

有时候我们会发现矩阵是矩形的，或者只有一层，这个时候就需要用几个通用的方法，来实现。例题：

LCR 146. 螺旋遍历二维数组

54. 螺旋矩阵

2326. 螺旋矩阵 IV

模拟路径法

我们先分析我们的转向条件：（1）当前进的方向上碰到了边界（2）当前进的方向上是已经走过的路径

第一个条件比较好解决，第二条件我们需要维护一个和数组相同大小的矩阵，走过的路线我们设置为true，没走过的设置为false.

由于我们的转向动作是有序的，是顺时针，所以我们可以使用一个数组来存储我们的方向。当到达转向条件时，设置成下一个转向动作。

vector<int> spiralArray(vector<vector<int>>& array) {if(array.empty()||array[0].empty()) //判断数组是否为空，注意先后顺序，array[0]在array为空时是不能访问的return {};int row = array.size();int col = array[0].size();int total = row*col;vector<vector<bool>> use(row,vector<bool>(col,0));  //路径表vector<int> ans(total,0);vector<vector<int>> direction{{0,1},{1,0},{0,-1},{-1,0}};   //方向表（顺时针）int directionIdx = 0;   //方向表索引int i=0,j=0;for(int k=0;k<total;k++){ans[k] = array[i][j];use[i][j] = true;int ni = i + direction[directionIdx][0];    //预更新iint nj = j + direction[directionIdx][1];    //预更新jif(ni<0||ni>=row||nj<0||nj>=col||use[ni][nj]==true){    //根据预更新状态判断转向条件directionIdx = (directionIdx+1)%4;  //转向则把方向索引设置到下一位}//实际更新i = i + direction[directionIdx][0];j = j + direction[directionIdx][1];}return ans;}

层级遍历法（边界收缩）

这个和刚刚用来解决方形矩阵的方法是相同的，只不过更新方式和更新条件要更加复杂。

一开始先设定好边界，当移动到边界的时候就转向，然后收缩边界。这样的好处在于我们不用再特意维护一个数组来判断路径是否被走过 了。因为走过的路径被我们收缩了，所以就不用在考虑。只需要在边界做检测就好了。

vector<vector<int>> spiralMatrix(int m, int n, ListNode* head) {vector<vector<int>> ans(m,vector<int>(n,-1));int top = 0;    int bottom = m-1;   //-1是因为索引和实际位置的差值int left = 0;int right = n-1;while(left<=right&&top<=bottom){    //如果相等就说明，边界收缩了，遍历结束了for(int i=left;i<=right;i++)    ans[top][i] = val;top++;                          //左上->右上 top边界收缩for(int i=top;i<=bottom;i++)ans[i][right] = val;right--;                        //右上->右下 right边界收缩for(int i=right;i>=left;i--)ans[bottom][i] = val;bottom--;                       //右下->左下 bottom边界收缩for(int i=bottom;i>=top;i--)ans[i][left] = val;left++;                         //左下->右上 left边界收缩}return ans;}

螺旋生成矩阵

这个算是一个小特例，大多数题目是给你一个矩阵让你去螺旋遍历，但是有的题目需要你自己螺旋生成一个矩阵。我们看到下面的例题：

885. 螺旋矩阵 III

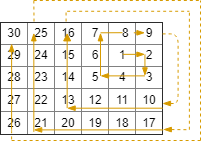
这道题需要我们形成一个螺旋的路径，然后返回矩形内的位置的坐标。难点在于这个螺旋路径的生成，因为转向的条件和每次前进的步长综合考虑起来条件会非常的复杂。下面的话给出两种方法。

边界扩展法

和我们之前所做的边界收缩相反，我们先界定好边界，然后每次转向时宽展这个方向上的边界。通过这种方式来动态的生成一个螺旋的路径

const int DIR[4][2] = {{0,1},{1,0},{0,-1},{-1,0}};
vector<vector<int>> spiralMatrixIII(int rows, int cols, int rStart, int cStart) {vector<vector<int>> ans;int total = rows*cols;int num = 1;int i = rStart,j = cStart;  //令i,j记录路径的实时位置int left = cStart - 1,right = cStart + 1,top = rStart - 1,bottom = rStart + 1;  //确定边界int dir=0;  //记录方向while(num <= total){if(i>=0&&i<rows&&j>=0&&j<cols){ //当路径到达矩阵内部时，记录当前位置ans.push_back({i,j});num++;}if(dir==0&&j==right){   //如果向右移动触碰右边界dir+=1;             //则转向right++;            //并拓展右边界}else if(dir==1&&i==bottom){    //如果向下移动触碰下边界dir+=1;                     //则转向bottom++;                   //并拓展下边界}else if(dir==2&&j==left){      //...dir+=1;left--;}else if(dir==3&&i==top){       //...dir=0;top--;}i += DIR[dir][0];       //根据方向来更新位置j += DIR[dir][1];}return ans;}

规律法

我们可以观察螺线路径的一个显著规律：每转向两次会更新一次前进的步长

const int DIR[4][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
vector<vector<int>> spiralMatrixIII(int R, int C, int r0, int c0) {int num=0;int dir=0;int run=2;  //步长计数器vector<vector<int>> ans;
​while(num < R * C){for(int i = 0; i < run / 2; i ++){   //遍历步长，每转两下就会增加一步if(r0 >= 0 && r0 < R && c0 >= 0 && c0 < C)ans.push_back({r0, c0}), ++ num;r0 += DIR[dir][0];c0 += DIR[dir][1];}pos = (pos + 1) % 4;    //每遍历一次步长，就转向run++;      //利用取整的性质，每转向两次才会增加一次步长}return ans;}

总结

螺旋矩阵的关键在于边界的检测和变换，还有转向条件的判断。比较简单。