辛普森悖论
第一步:概念拆解
想象你在比较两个班级的考试成绩:
- 第一天:实验组(1个学生考了90分),对照组(99个学生平均考了80分)
- 第二天:实验组(50个学生平均考了70分),对照组(50个学生平均考了60分)
如果简单把两天的分数加起来算总平均: - 实验组:(90 + 70×50)/51 ≈ 70.4分
- 对照组:(80×99 + 60×50)/149 ≈ 72.3分
奇怪的事情发生了:明明实验组每天都比对照组考得好,但合起来看反而更差!
第二步:关键矛盾点
就像比较两个餐厅的满意度:
- 工作日:高档餐厅(客人少但评分高),快餐店(客人多评分略低)
- 周末:两家客流量相同,高档餐厅评分仍更高
但如果忽略时间维度,直接合并数据:
快餐店会因为工作日的大量客流拉高总平均分,掩盖了高档餐厅每天的真实优势。
第三步:统计学本质
辛普森悖论的核心是混淆变量(这里是"日期"):
- 第一天实验组只有1%流量,这部分用户可能是高质量种子用户(转化率2.3%极高)
- 第二天50%流量包含大量普通用户(转化率降至1.2%)
- 合并时,实验组数据被第二天的大量普通用户稀释,而对照组数据仍被第一天的高权重优质用户支撑
第四步:解决方案
避免错误的三步法:
- 分层比较:分别看第一天/第二天的结果(保持流量比例一致)
- 加权计算:按天数分配权重(如每天算50%贡献)
- 因果图分析:画流程图确认"日期"是否影响流量分配与转化率的关系
就像比较两种药物的疗效时,必须考虑试验阶段的重症/轻症患者比例变化,否则会得出"救人更多的药反而总死亡率更高"的荒谬结论。
内容类AB实验案例分析
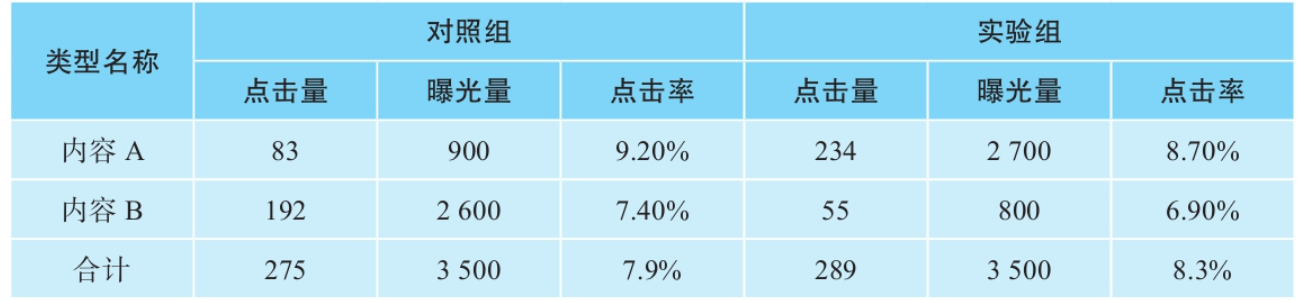
看一个内容类AB实验的例子,某资讯内容产品在列表包括AB两类内容,某实验做了A类内容的提权,也就是提升了A类内容的曝光占比,实验关心的核心指标是点击率。
1)实验提升了整体的点击率吗?
2)通过数据推测实验为什么会出现A、B的点击率都下降的现象。
3)这种提升点击率的方法可能有什么潜在的问题?
第一步:用买菜比喻理解基础概念
想象菜市场有两个摊位:
- 摊位A(精品蔬菜):每天摆10斤能卖9斤(点击率90%)
- 摊位B(普通蔬菜):每天摆100斤能卖70斤(点击率70%)
某天市场经理决定:
- 给摊位A多分配货架(从10斤→30斤)
- 摊位B被迫减少到80斤
结果发现:
- 摊位A销量变成25斤(点击率降到83%)
- 摊位B销量变成55斤(点击率降到68%)
- 但总销售额却从79斤增加到80斤!
第二步:拆解三个问题的本质

问题1:整体点击率提升了吗?
- 对照组:A(9.2%) + B(7.4%) → 加权平均=(83+192)/(900+2600)=7.9%
- 实验组:A(8.7%) + B(6.9%) → 加权平均=(234+55)/(2700+800)=8.3%
→ 确实提升了0.4%,就像菜市场总销售额增加
问题2:为什么AB各自点击率都降?
对A内容:曝光量从900→2700(3倍!)
- 用户看到太多同类内容产生审美疲劳(如同连续吃3天精品菜也会腻)
- 新曝光的用户可能不是A的理想受众(像把精品菜卖给只想买便宜菜的人)
对B内容:曝光量从2600→800(被挤压)
- 用户注意力被更多A内容吸引(像顾客都被精品菜摊位的促销吸引)
- 剩余曝光可能给了B的非目标用户(像只有匆匆路过的人才会买剩下的普通菜)
问题3:潜在问题是什么?
数据假象:就像菜市场总销售额增加,但:
- 可能牺牲了老顾客体验(天天被迫看同类内容)
- 新用户可能因内容单一而流失
生态破坏:
- 如果A是标题党内容,长期会降低内容质量
- B类优质内容得不到曝光(如同菜市场再也买不到小众但健康的食材)
指标陷阱:
- 点击率提升但阅读时长可能下降
- 用户满意度等隐性指标无法体现
第三步:用控制变量法看本质
如果把实验组数据按对照组比例还原:
- 假设保持A:B=900:2600的比例
- 实验组A应有289×(900/3500)=74.3点击(实际234,严重偏离)
- 实验组B应有289×(2600/3500)=214.7点击(实际55,严重偏离)
→ 证明流量分配变化才是核心影响因素
第四步:给产品经理的建议
- 分层实验:对不同用户群体分别测试(如新用户/老用户)
- 动态加权:根据用户偏好实时调整AB比例
- 多指标监控:配合阅读深度、分享率等综合评估
- 内容质量检测:建立A类内容的"标题党指数"预警机制
就像调整菜市场摊位不能只看总销售额,还要考虑顾客复购率、摊位多样性、菜品质量等。这个案例生动展示了:局部最优≠全局最优,需要警惕"提升一个指标,毁掉整个生态"的陷阱。
)


中设置中文界面)















|SVM-拉格朗日乘数法理解)