【深度学习】神经网络-part2

一、数据加载器

数据集和加载器

1.1构建数据类

1.1.1 Dataset类

Dataset是一个抽象类，是所有自定义数据集应该继承的基类。它定义了数据集必须实现的方法。

必须实现的方法

__len__: 返回数据集的大小
__getitem__: 支持整数索引，返回对应的样本

构建自定义数据加载类通常需要继承 torch.utils.data.Dataset

__init__ 方法 用于初始化数据集对象：通常在这里加载数据，或者定义如何从存储中获取数据的路径和方法。
```
def __init__(self, data, labels):self.data = dataself.labels = labels
```
__len__ 方法 返回样本数量：需要实现，以便 Dataloader加载器能够知道数据集的大小。
```
def __len__(self):return len(self.data)
```
__getitem__ 方法 根据索引返回样本：将从数据集中提取一个样本，并可能对样本进行预处理或变换。
```
def __getitem__(self, index):sample = self.data[index]label = self.labels[index]return sample, label
```
代码参考

import torch
import torch.nn as nn
from torch.utils.data import Dataset, DataLoader# 定义数据加载类
# 把“数据 + 标签”包成一个 Dataset
class CustomDataset(Dataset):def __init__(self, data, labels):self.data = dataself.labels = labelsdef __len__(self):return len(self.data)def __getitem__(self, index):index = min(max(index, 0), len(self.data) - 1)sample = self.data[index]label = self.labels[index]return sample, labeldef test001():# 简单的数据集准备data_x = torch.randn(666, 20, requires_grad=True, dtype=torch.float32)data_y = torch.randn(data_x.shape[0], 1, dtype=torch.float32)dataset = CustomDataset(data_x, data_y)# 随便打印个数据看一下print(dataset[0])if __name__ == "__main__":test001()
'''这段代码没有训练、没有模型、没有 DataLoader，只是演示：
“怎样把随机张量包装成自定义 Dataset，并取出第一条看看长啥样”。'''

1.1.2 TensorDataset类

使Dataset的简单实现，封装了张量数据，适用数据已经是张量的情况

特点：

简单快捷：当数据已经是张量形式时，无需自定义Dataset类
多张量支持：可以接受多个张量作为输入，按顺序返回
索引一致：所有张量的第一个维度必须相同，表示样本数量

class TensorDataset(Dataset):def __init__(self, *tensors):# size(0)在python中同shape[0]，获取的是样本数量# 用第一个张量中的样本数量和其他张量对比，如果全部相同则通过断言，否则抛异常assert all(tensors[0].size(0) == tensor.size(0) for tensor in tensors)self.tensors = tensorsdef __getitem__(self, index):return tuple(tensor[index] for tensor in self.tensors)def __len__(self):return self.tensors[0].size(0)
def test03():torch.manual_seed(0)# 创建特征张量和标签张量features = torch.randn(100, 5)  # 100个样本，每个样本5个特征labels = torch.randint(0, 2, (100,))  # 100个二进制标签# print(labels)# 创建TensorDatasetdataset = TensorDataset(features, labels)# 使用方式与自定义Dataset相同print(len(dataset))  # 输出: 100print(dataset[0])  # 输出: (tensor([...]), tensor(0))
test03()

1.2 数据加载器

DataLoader是一个迭代器用于从Dataset中批量加载数据

批量加载：将多个样本组合成一个批次。

打乱数据：在每个 epoch 中随机打乱数据顺序。

多线程加载：使用多线程加速数据加载。

# 创建 DataLoader
dataloader = DataLoader(
dataset, # 数据集
batch_size=10, # 批量大小
shuffle=True, # 是否打乱数据
num_workers=2 # 使用 2 个子进程加载数据
)

# 遍历 DataLoader
# enumerate返回一个枚举对象（iterator），生成由索引和值组成的元组
for batch_idx, (samples, labels) in enumerate(dataloader):
print(f"Batch {batch_idx}:")
print("Samples:", samples)
print("Labels:", labels)

示例：

import torch
import torch.nn as nn
from torch.utils.data import Dataset, DataLoader# 定义数据加载类
class CustomDataset(Dataset):def __init__(self, data, labels):self.data = dataself.labels = labelsdef __len__(self):return len(self.data)def __getitem__(self, index):index = min(max(index, 0), len(self.data) - 1)sample = self.data[index]label = self.labels[index]return sample, labeldef test01():# 简单的数据集准备# 666 条样本，每条 20 维特征data_x = torch.randn(666, 20, requires_grad=True, dtype=torch.float32)data_y = torch.randn(data_x.size(0), 1, dtype=torch.float32)dataset = CustomDataset(data_x, data_y)# 构建数据加载器data_loader = DataLoader(dataset, batch_size=7, shuffle=True)for i,(batch_x, batch_y) in enumerate(data_loader):print(batch_x, batch_y)breaktest01()

2 数据集加载案例

2.1 加载csv数据集

import torch
from torch.utils.data import Dataset, DataLoader
import pandas as pdclass MyCsvDataset(Dataset):def __init__(self, filename):df = pd.read_csv(filename)# 删除文字列df = df.drop(["学号", "姓名"], axis=1)# 转换为tensordata = torch.tensor(df.values)# 最后一列以前的为data，最后一列为labelself.data = data[:, :-1]self.label = data[:, -1]self.len = len(self.data)def __len__(self):return self.lendef __getitem__(self, index):idx = min(max(index, 0), self.len - 1)  # 1. 防止越界return self.data[idx], self.label[idx]  # 2. 返回该索引对应的特征和标签def test001():excel_path = r"./大数据答辩成绩表.csv"dataset = MyCsvDataset(excel_path)dataloader = DataLoader(dataset, batch_size=4, shuffle=True)for i, (data, label) in enumerate(dataloader):print(i, data, label)if __name__ == "__main__":test001()

或者

class TensorDataset(Dataset):def __init__(self,*tensors):assert all(t.shape[0]==tensors[0].shape[0] for t in tensors)self.tensors = tensorsdef __getitem__(self, index):return tuple(t[index] for t in self.tensors)def __len__(self):return self.tensors[0].shape[0]def build_dataset(filepath):df = pd.read_csv(filepath)df.drop(columns=['学号', '姓名'], inplace=True)data = df.iloc[..., :-1]labels = df.iloc[..., -1]x = torch.tensor(data.values, dtype=torch.float)y = torch.tensor(labels.values)dataset = TensorDataset(x, y)return datasetdef test001():filepath = r"./大数据答辩成绩表.csv"dataset = build_dataset(filepath)dataloader = DataLoader(dataset, batch_size=4, shuffle=True)for i, (data, label) in enumerate(dataloader):print(i, data, label)
test001()

2.2 加载图片数据集

用ImageFloder

ImageFolder 会根据文件夹的结构来加载图像数据。它假设每个子文件夹对应一个类别，文件夹名称即为类别名称

root 是根目录。

class1、class2 等是类别名称。

每个类别文件夹中的图像文件会被加载为一个样本。

ImageFolder构造函数如下：

torchvision.datasets.ImageFolder(root, transform=None, target_transform=None, is_valid_file=None)

参数解释

root：字符串，指定图像数据集的根目录。

transform：可选参数，用于对图像进行预处理。通常是一个 torchvision.transforms 的组合。

target_transform：可选参数，用于对目标（标签）进行转换。

is_valid_file：可选参数，用于过滤无效文件。如果提供，只有返回 True 的文件才会被加载。

2.3 加载官方数据集

在 PyTorch 中官方提供了一些经典的数据集，如 CIFAR-10、MNIST、ImageNet 等，可以直接使用这些数据集进行训练和测试。

数据集：Datasets — Torchvision 0.22 documentation

常见数据集：

MNIST: 手写数字数据集，包含 60,000 张训练图像和 10,000 张测试图像。

CIFAR10: 包含 10 个类别的 60,000 张 32x32 彩色图像，每个类别 6,000 张图像。

CIFAR100: 包含 100 个类别的 60,000 张 32x32 彩色图像，每个类别 600 张图像。

COCO: 通用对象识别数据集，包含超过 330,000 张图像，涵盖 80 个对象类别。

torchvision.transforms 和 torchvision.datasets 是 PyTorch 中处理计算机视觉任务的两个核心模块，它们为图像数据的预处理和标准数据集的加载提供了强大支持。

transforms 模块提供了一系列用于图像预处理的工具，可以将多个变换组合成处理流水线。

datasets 模块提供了多种常用计算机视觉数据集的接口，可以方便地下载和加载。

四、激活函数

在隐藏层引入非线性，使得神经网络能够学习和表示复杂的函数关系，使网络具备非线性能力 。

4.1基础概念

4.1.1 线性理解

如果在隐藏层不使用激活函数，那么整个神经网络会表现为一个线性模型。我们可以通过数学推导来展示这一点。

假设：

神经网络有L 层，每层的输出为 \mathbf{a}^{(l)}。
每层的权重矩阵为 \mathbf{W}^{(l)} ，偏置向量为\mathbf{b}^{(l)}。
输入数据为\mathbf{x}，输出为\mathbf{a}^{(L)}。

一层网络的情况

对于单层网络（输入层到输出层），如果没有激活函数，输出\mathbf{a}^{(1)} 可以表示为： \mathbf{a}^{(1)} = \mathbf{W}^{(1)} \mathbf{x} + \mathbf{b}^{(1)}

两层网络的情况

假设我们有两层网络，且每层都没有激活函数，则：

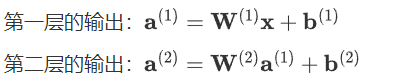
多层网络的情况

如果有L层，每层都没有激活函数，则第l层的输出为：

通过递归代入，可以得到：

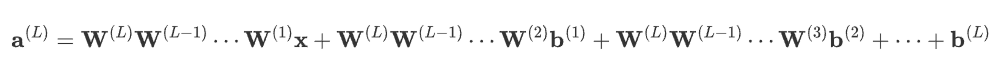
表达式可简化为：

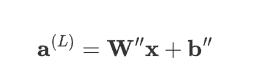
其中，\mathbf{W}'' 是所有权重矩阵的乘积，\mathbf{b}''是所有偏置项的线性组合。

如此可以看得出来，无论网络多少层，意味着：

整个网络就是线性模型，无法捕捉数据中的非线性关系。

激活函数是引入非线性特性、使神经网络能够处理复杂问题的关键。

1.2 非线性可视化

2 常见激活函数

2.1 sigmoid

是非常常见的非现金激活函数，特别是早期神经网络应用中，它将输入映射到0到1之前，非常适合处理概率问题

2.2.1 公式

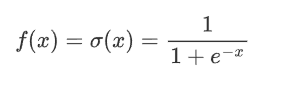
其中，e 是自然常数（约等于2.718），x 是输入。

2.1.2 特征

1 将任意输入的数映射到0到1之间非常适合处理概率场景

2 sigmoid一般只用于二分类的输出层

3 导数计算比较方便可以自身表达式表示

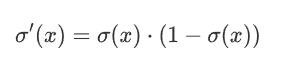
2.1.3 缺点

梯度消失

在输入非常大或非常小时，Sigmoid函数的梯度会变得非常小，接近于0。这导致在反向传播过程中，梯度逐渐衰减。

最终使得早期层的权重更新非常缓慢，进而导致训练速度变慢甚至停滞。

信息丢失

输入100和输入10000经过sigmoid的激活值几乎都是等于 1 的，但是输入的数据却相差 100 倍。

计算成本高

由于涉及指数运算，Sigmoid的计算比ReLU等函数更复杂，尽管差异并不显著

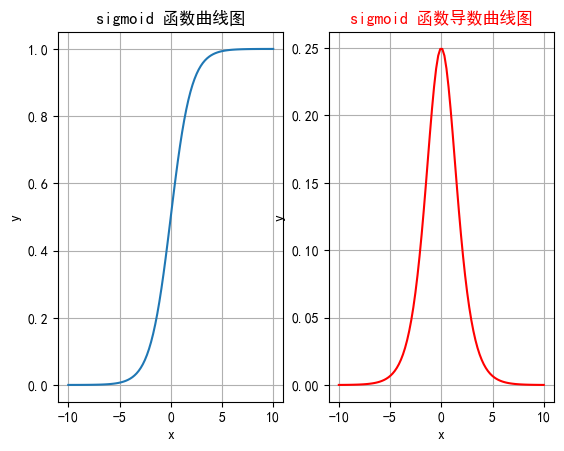
2.1.4 函数绘制

import torch
import matplotlib.pyplot as plt# plt支持中文
plt.rcParams["font.sans-serif"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = Falsedef test001():# 一行两列绘制图像_, ax = plt.subplots(1, 2)# 绘制函数图像x = torch.linspace(-10, 10, 100)y = torch.sigmoid(x)# 网格ax[0].grid(True)ax[0].set_title("sigmoid 函数曲线图")ax[0].set_xlabel("x")ax[0].set_ylabel("y")# 在第一行第一列绘制sigmoid函数曲线图ax[0].plot(x, y)# 绘制sigmoid导数曲线图x = torch.linspace(-10, 10, 100, requires_grad=True)# 自动求导# torch.sigmoid(x).sum().backward()ax[1].grid(True)ax[1].set_title("sigmoid 函数导数曲线图", color="red")ax[1].set_xlabel("x")ax[1].set_ylabel("y")# 用自动求导的结果绘制曲线图ax[1].plot(x.detach().numpy(), x.grad.detach().numpy())# 设置曲线颜色ax[1].lines[0].set_color("red")plt.show()if __name__ == "__main__":test001()

2.2 tanh

双曲正切是一种常见的非线性激活函数，tanh 函数也是一种S形曲线，输出范围为(−1,1)。

2.2.1 公式

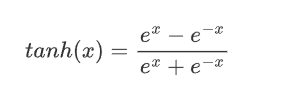
2.2.2 特征

输出范围: 将输入映射到(-1, 1)之间，因此输出是零中心的。相比于Sigmoid函数，这种零中心化的输出有助于加速收敛。
对称性: Tanh函数是关于原点对称的奇函数，因此在输入为0时，输出也为0。这种对称性有助于在训练神经网络时使数据更平衡。
平滑性: Tanh函数在整个输入范围内都是连续且可微的，这使其非常适合于使用梯度下降法进行优化。

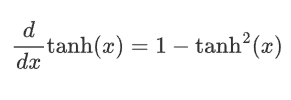
2.2.3 缺点

梯度消失: 虽然一定程度上改善了梯度消失问题，但在输入值非常大或非常小时导数还是非常小，这在深层网络中仍然是个问题。这是因为每一层的梯度都会乘以一个小于1的值，经过多层乘积后，梯度会变得非常小，导致训练过程变得非常缓慢，甚至无法收敛。
计算成本: 由于涉及指数运算，Tanh的计算成本还是略高，尽管差异不大。

2.2.4 函数绘制

import torch
import matplotlib.pyplot as plt# plt支持中文
plt.rcParams["font.sans-serif"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = Falsedef test001():# 一行两列绘制图像_, ax = plt.subplots(1, 2)# 绘制函数图像x = torch.linspace(-10, 10, 100)y = torch.tanh(x)# 网格ax[0].grid(True)ax[0].set_title("tanh 函数曲线图")ax[0].set_xlabel("x")ax[0].set_ylabel("y")# 在第一行第一列绘制tanh函数曲线图ax[0].plot(x, y)# 绘制tanh导数曲线图x = torch.linspace(-10, 10, 100, requires_grad=True)# 自动求导：需要标量才能反向传播torch.tanh(x).sum().backward()ax[1].grid(True)ax[1].set_title("tanh 函数导数曲线图", color="red")ax[1].set_xlabel("x")ax[1].set_ylabel("x.grad")# 用自动求导的结果绘制曲线图ax[1].plot(x.detach().numpy(), x.grad.detach().numpy())# 设置曲线颜色ax[1].lines[0].set_color("red")plt.show()if __name__ == "__main__":test001()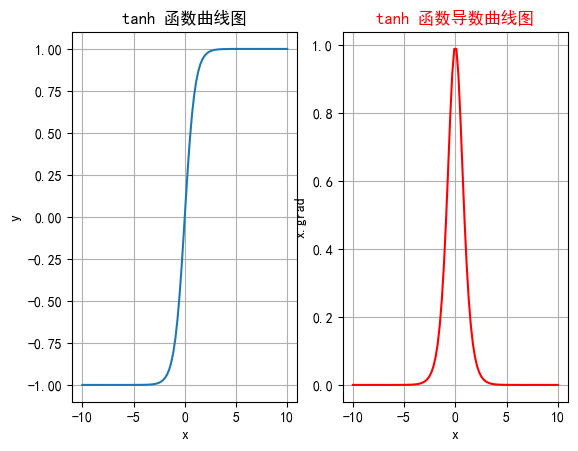

2.3 ReLU

深度学习中最常用的激活函数之一，它的全称是修正线性单元 ，ReLU 激活函数的定义非常简单，但在实践中效果非常好。

2.3.1 公式

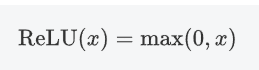
即ReLU对输入x进行非线性变换：

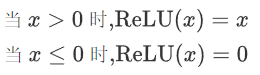
2.3.2 特征

计算简单：ReLU 的计算非常简单，只需要对输入进行一次比较运算，这在实际应用中大大加速了神经网络的训练。
ReLU 函数的导数是分段函数：
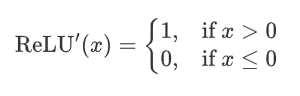
缓解梯度消失问题：相比于 Sigmoid 和 Tanh 激活函数，ReLU 在正半区的导数恒为 1，这使得深度神经网络在训练过程中可以更好地传播梯度，不存在饱和问题。
稀疏激活：ReLU在输入小于等于 0 时输出为 0，这使得 ReLU 可以在神经网络中引入稀疏性（即一些神经元不被激活），这种稀疏性可以减少网络中的冗余信息，提高网络的效率和泛化能力。

2.3.3 缺点

神经元死亡：由于ReLU在x≤0时输出为0，如果某个神经元输入值是负，那么该神经元将永远不再激活，成为“死亡”神经元。随着训练的进行，网络中可能会出现大量死亡神经元，从而会降低模型的表达能力。

2.3.4 函数绘图

import torch
import torch.nn.functional as F
import matplotlib.pyplot as plt# 中文问题
plt.rcParams["font.sans-serif"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = Falsedef test006():# 输入数据xx = torch.linspace(-20, 20, 1000)y = F.relu(x)# 绘制一行2列_, ax = plt.subplots(1, 2)ax[0].plot(x.numpy(), y.numpy())# 显示坐标格子ax[0].grid()ax[0].set_title("relu 激活函数")ax[0].set_xlabel("x")ax[0].set_ylabel("y")# 绘制导数函数x = torch.linspace(-20, 20, 1000, requires_grad=True)F.relu(x).sum().backward()ax[1].plot(x.detach().numpy(), x.grad.detach().numpy())ax[1].grid()ax[1].set_title("relu 激活函数导数", color="red")# 设置绘制线色颜色ax[1].lines[0].set_color("red")ax[1].set_xlabel("x")ax[1].set_ylabel("x.grad")plt.show()if __name__ == "__main__":test006()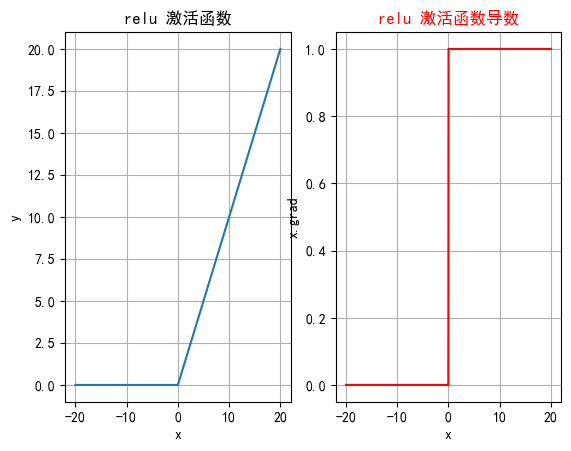

2.4 LeakyReLu

是ReLue函数的改进，解决ReLU的一些缺点，比如Dying ReLu，Leaky ReLU 通过在输入为负时引入一个小的负斜率来改善这一问题。

2.4.1 公式

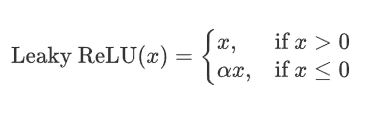
其中，alpha 是一个非常小的常数（如 0.01），它控制负半轴的斜率。这个常数 \alpha是一个超参数，可以在训练过程中可自行进行调整。

2.4.2 特征

避免神经元死亡：通过在x\leq 0 区域引入一个小的负斜率，这样即使输入值小于等于零，Leaky ReLU仍然会有梯度，允许神经元继续更新权重，避免神经元在训练过程中完全“死亡”的问题。
计算简单：Leaky ReLU 的计算与 ReLU 相似，只需简单的比较和线性运算，计算开销低。

2.4.3 缺点

参数选择：\alpha 是一个需要调整的超参数，选择合适的\alpha 值可能需要实验和调优。
出现负激活：如果\alpha 设定得不当，仍然可能导致激活值过低。

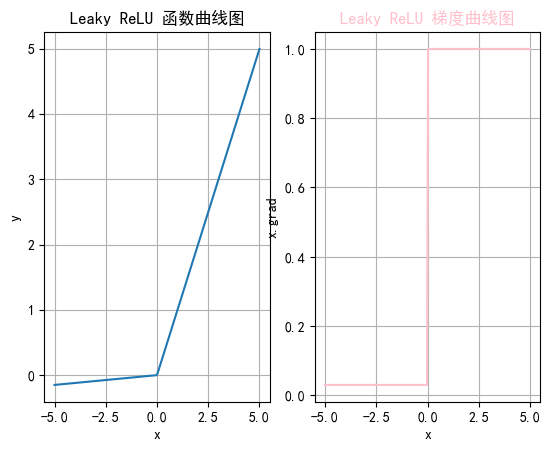
2.4.4 函数绘制

import torch
import torch.nn.functional as F
import matplotlib.pyplot as plt# 中文设置
plt.rcParams["font.sans-serif"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = Falsedef test006():x = torch.linspace(-5, 5, 200)# 设置leaky_relu的负斜率超参数slope = 0.03y = F.leaky_relu(x, slope)# 一行两列_, ax = plt.subplots(1, 2)# 开始绘制函数曲线图ax[0].plot(x, y)ax[0].set_title("Leaky ReLU 函数曲线图")ax[0].set_xlabel("x")ax[0].set_ylabel("y")ax[0].grid(True)# 绘制leaky_relu的梯度曲线图x = torch.linspace(-5, 5, 200, requires_grad=True)F.leaky_relu(x, slope).sum().backward()ax[1].plot(x.detach().numpy(), x.grad.detach().numpy())ax[1].set_title("Leaky ReLU 梯度曲线图", color="pink")ax[1].set_xlabel("x")ax[1].set_ylabel("x.grad")ax[1].grid(True)# 设置线的颜色ax[1].lines[0].set_color("pink")plt.show()if __name__ == "__main__":test006()

2.5 softmax

通常用于分类问题的输出层，它能将网络的输出转化为概率分布，使得输出的各个类别的概率之和为 1。Softmax 特别适合用于多分类问题。

2.5.1 公式

假设神经网络的输出层有n个节点，每个节点的输入为z_i，则 Softmax 函数的定义如下

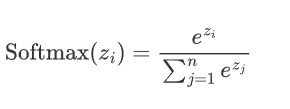
给定输入向量

1.指数变换：对每个 $z_i$进行指数变换，得到，使z的取值区间从变为

2.将所有指数变换后的值求和，得到

3.将t中每个除以归一化因子s，得到概率分布:

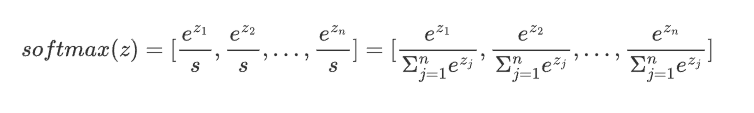
即：

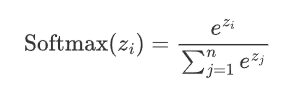
从上述公式可以看出：

1. 每个输出值在 (0,1)之间

2. Softmax()对向量的值做了改变，但其位置不变

3. 所有输出值之和为1，即

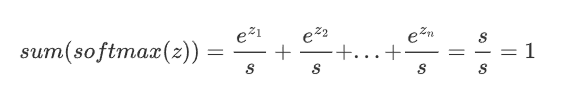
2.5.2 特征

将输出转化为概率：通过Softmax，可以将网络的原始输出转化为各个类别的概率，从而可以根据这些概率进行分类决策。

将输出转化为概率：通过Softmax，可以将网络的原始输出转化为各个类别的概率，从而可以根据这些概率进行分类决策。
概率分布：Softmax的输出是一个概率分布，即每个输出值\text{Softmax}(z_i)都是一个介于0和1之间的数，并且所有输出值的和为 1：
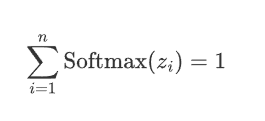
突出差异：Softmax会放大差异，使得概率最大的类别的输出值更接近1，而其他类别更接近0。
在实际应用中，Softmax常与交叉熵损失函数Cross-Entropy Loss结合使用，用于多分类问题。在反向传播中，Softmax的导数计算是必需的。

2.5.3 缺点

数值不稳定性：在计算过程中，如果z_i的数值过大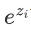，可能会导致数值溢出。因此在实际应用中，经常会对z_i进行调整，如减去最大值以确保数值稳定。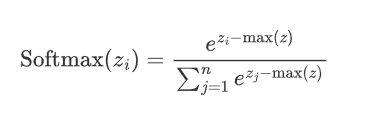

在 PyTorch 中，torch.nn.functional.softmax 函数就自动处理了数值稳定性问题。

2.难以处理大量类别：Softmax在处理类别数非常多的情况下（如大模型中的词汇表）计算开销会较大。

2.5.4 代码实现

import torch
import torch.nn as nn# 表示4分类，每个样本全连接后得到4个得分，下面示例模拟的是两个样本的得分
input_tensor = torch.tensor([[-1.0, 2.0, -3.0, 4.0], [-2, 3, -3, 9]])softmax = nn.Softmax()
output_tensor = softmax(input_tensor)
# 关闭科学计数法
torch.set_printoptions(sci_mode=False)
print("输入张量:", input_tensor)
print("输出张量:", output_tensor)