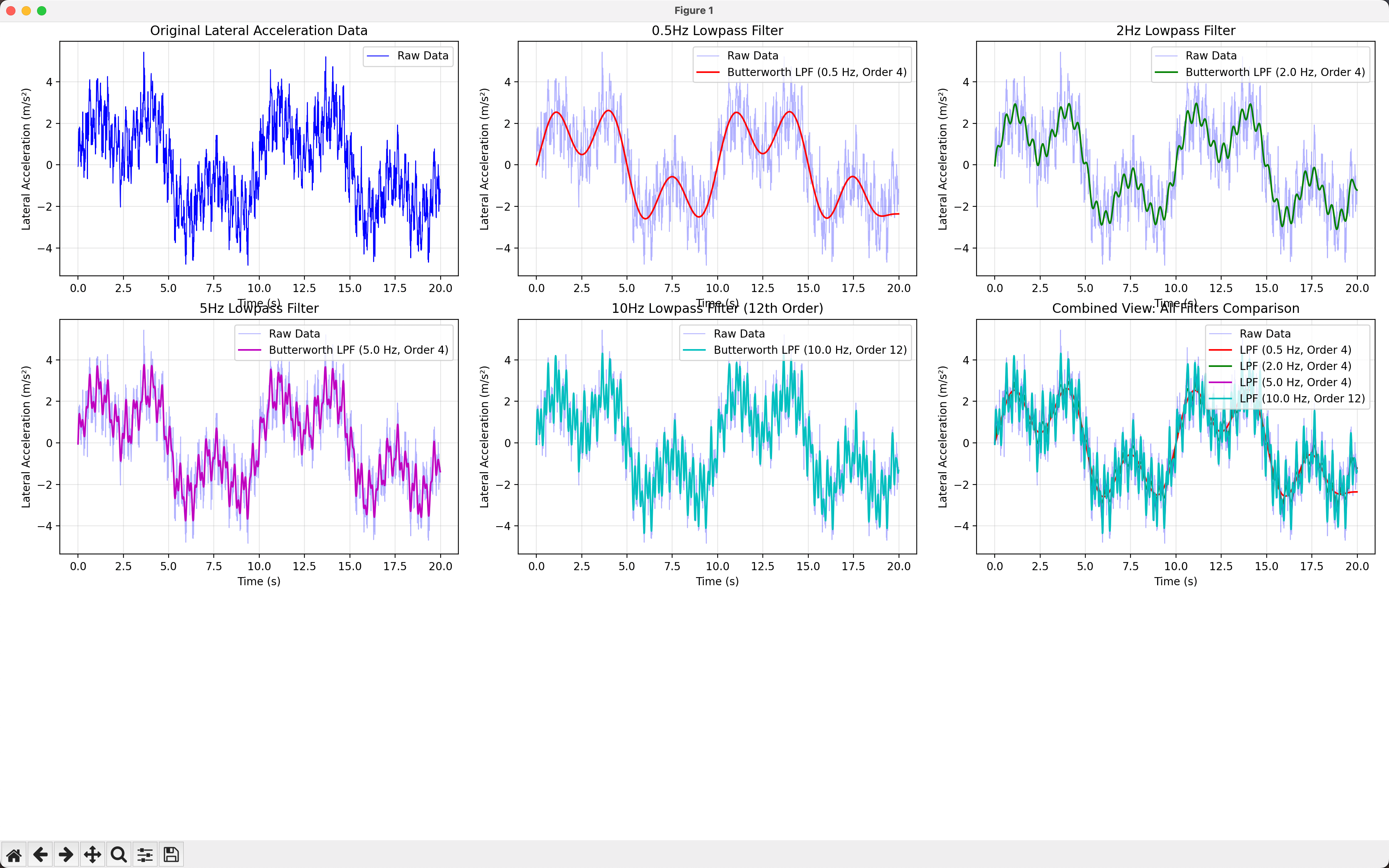
在自动驾驶的宏大叙事中,我们常常聚焦于人工智能、深度学习、高精地图等"明星技术"。然而,在这些耀眼的光环背后,有一个低调却至关重要的"幕后英雄"——滤波器。它不仅是信号处理的工具,更是连接物理世界与数字算法的桥梁,是自动驾驶感知、决策、控制乃至测试验证的数学基石。
本文将带你深入滤波器的世界,从车辆加速度的噪声抑制,到其在自动驾驶系统中的核心应用,再到测试验证中的关键抉择,揭示其如何从一个简单的数学公式,演变为决定系统成败的"双刃剑"。我们将补充常用滤波器的核心公式,并提供不同应用场景下的选择指南。
第一重境界:降噪——让信号回归真实
想象一辆车在颠簸的路面上行驶。其搭载的加速度计会忠实地记录下每一个微小的振动——轮胎碾过石子、悬挂系统弹跳、发动机抖动。这些高频噪声,与车辆真正加速、减速或转弯产生的低频惯性力混杂在一起,形成了我们常说的"脏信号"。
如果直接使用这种信号计算速度或位移,高频噪声会在积分过程中被急剧放大,导致结果严重失真。例如,一次平稳的刹车过程,可能在计算出的"速度曲线"上表现为剧烈的震荡。这便是滤波器登场的时刻。
目标:保留反映车辆真实运动的低频信息,抑制无用的高频噪声。
常用方法与核心公式:
| 滤波器类型 | 核心公式 | 说明 |
|---|---|---|
| 移动平均 (Moving Average) | y[n]=1N∑k=0N−1x[n−k] y[n] = \frac{1}{N} \sum_{k=0}^{N-1} x[n-k] y[n]=N1k=0∑N−1x[n−k] | 计算最近N个采样点的算术平均。实现简单,但延迟大(约 N−12\frac{N-1}{2}2N−1 个周期),会削弱信号峰值。 |
| 一阶低通 (First-Order Low-Pass) | y[n]=α⋅x[n]+(1−α)⋅y[n−1] y[n] = \alpha \cdot x[n] + (1 - \alpha) \cdot y[n-1] y[n]=α⋅x[n]+(1−α)⋅y[n−1] 其中 α=dtτ+dt,τ=12πfc \alpha = \frac{dt}{\tau + dt},\quad \tau = \frac{1}{2\pi f_c} α=τ+dtdt,τ=2πfc1 | dt为采样周期,fc为截止频率。通过调整fc控制平滑程度。相位延迟小于移动平均,广泛用于车载ECU。 |
| 卡尔曼滤波 (Kalman Filter) | 预测: x^−[k]=Fx^[k−1]+Bu[k] \hat{\mathbf{x}}^{-}[k] = \mathbf{F}\hat{\mathbf{x}}[k-1] + \mathbf{B}\mathbf{u}[k] x^−[k]=Fx^[k−1]+Bu[k] P−[k]=FP[k−1]FT+Q \mathbf{P}^{-}[k] = \mathbf{F}\mathbf{P}[k-1]\mathbf{F}^T + \mathbf{Q} P−[k]=FP[k−1]FT+Q 更新: K[k]=P−[k]HT(HP−[k]HT+R)−1 \mathbf{K}[k] = \mathbf{P}^{-}[k]\mathbf{H}^T(\mathbf{H}\mathbf{P}^{-}[k]\mathbf{H}^T + \mathbf{R})^{-1} K[k]=P−[k]HT(HP−[k]HT+R)−1 x^[k]=x^−[k]+K[k](z[k]−Hx^−[k]) \hat{\mathbf{x}}[k] = \hat{\mathbf{x}}^{-}[k] + \mathbf{K}[k](\mathbf{z}[k] - \mathbf{H}\hat{\mathbf{x}}^{-}[k]) x^[k]=x^−[k]+K[k](z[k]−Hx^−[k]) P[k]=(I−K[k]H)P−[k] \mathbf{P}[k] = (\mathbf{I} - \mathbf{K}[k]\mathbf{H})\mathbf{P}^{-}[k] P[k]=(I−K[k]H)P−[k] | 线性系统的最优估计算法。F\mathbf{F}F为状态转移矩阵,H\mathbf{H}H为观测矩阵,Q\mathbf{Q}Q和R\mathbf{R}R分别为过程噪声和观测噪声协方差。需要建立准确的系统模型。 |
| 扩展卡尔曼滤波 (EKF) | 同KF,但F\mathbf{F}F和H\mathbf{H}H替换为非线性函数f()f()f()和h()h()h()的雅可比矩阵。 | 用于非线性系统(如车辆运动学)。通过局部线性化近似处理非线性。 |
| 互补滤波 (Complementary Filter) | θest=α⋅(θprev+ω⋅dt)+(1−α)⋅θacc \theta_{est} = \alpha \cdot (\theta_{prev} + \omega \cdot dt) + (1 - \alpha) \cdot \theta_{acc} θest=α⋅(θprev+ω⋅dt)+(1−α)⋅θacc | 融合陀螺仪(高频准)和加速度计(低频准)。ω\omegaω为角速度,θacc\theta_{acc}θacc为由加速度计计算的姿态角。α\alphaα通常接近1。 |
本质:这一境界的滤波器,是信号的"清洁工",旨在还原物理世界的真实动态。
第二重境界:融合——在不确定性中构建认知
当自动驾驶车辆驶上道路,它不再仅仅依赖单一传感器。激光雷达、摄像头、毫米波雷达、GPS、IMU、轮速计……多种传感器从不同维度感知环境。然而,每个传感器都有其局限:摄像头怕暗,雷达角分辨率低,GPS在隧道中失效,IMU积分会漂移。
此时,滤波器的角色从"清洁工"升级为**“融合大师”**。它利用数学工具,在不确定性中构建对世界最可能的认知。
核心应用场景:
- 环境感知与目标跟踪:使用KF/EKF预测动态目标轨迹,维持ID连续性。
- 高精度定位:通过EKF/UKF融合RTK-GPS、IMU、轮速计,实现厘米级定位。
- 车辆状态估计:用EKF估计侧滑角、真实速度;用互补滤波分离重力分量。
本质:这一境界的滤波器,是系统的"小脑",负责协调多源信息,生成连贯、可靠的状态估计,为决策提供坚实基础。
第三重境界:抉择——测试中的双刃剑
在自动驾驶的研发闭环中,测试验证是确保安全的最终防线。然而,测试工程师面临一个悖论:原始数据充满噪声,难以分析;但滤波处理又可能扭曲事实,掩盖问题。
滤波器在此刻成为一把"双刃剑":
- 用得好:它是"数据医生",能生成高精度真值、准确评估性能、辅助故障诊断。
- 用得不好:它是"遮羞布",可能抹平紧急制动的峰值、掩盖传感器的周期性抖动,让测试结果失去意义。
如何科学选择滤波器?——场景化决策指南
选择滤波器必须基于明确的测试目标。以下是常见测试场景下的推荐策略:
| 测试目标 | 关键分析需求 | 推荐滤波器 | 参数建议与注意事项 |
|---|---|---|---|
| AEB/FCW功能触发评估 | 精确的相对距离、相对速度变化率,捕捉瞬时事件。 | 轻度一阶低通 或 零相位低通 | 截止频率:10-20 Hz。 禁止重度滤波!需保留刹车尖峰。建议同时展示原始与滤波后信号对比。 |
| 乘坐舒适性分析 (Ride Comfort) | 人体感知的低频晃动(点头、俯仰、横摆),抑制高频路面噪声。 | 中度一阶低通 或 带阻滤波器 | 截止频率:3-5 Hz。 若存在明显发动机共振(如30Hz),使用带阻滤波器精准切除。 |
| 高精度轨迹生成 (Ground Truth) | 厘米级绝对位置、速度、姿态,长期稳定性。 | 扩展卡尔曼滤波器 (EKF) | 必须融合RTK-GPS、高精度IMU、轮速计。 仔细标定噪声协方差 Q\mathbf{Q}Q 和 R\mathbf{R}R。 |
| 能耗与续航测试 | 平均加速度、宏观速度曲线,对瞬时抖动不敏感。 | 重度一阶低通 或 移动平均 | 截止频率:1-2 Hz 或 N=50-100 的移动平均。 目标是得到平滑的宏观趋势。 |
| 传感器故障诊断 | 分析原始噪声的频谱、方差、周期性,定位干扰源。 | 禁止滤波 | 必须使用原始信号进行FFT频谱分析、统计分析。 滤波会"擦除"故障证据。 |
| 规划控制算法验证 | 平滑的车辆状态输入,避免控制器因噪声抖动。 | 实时一阶低通 或 EKF | 截止频率:5-10 Hz。 注意相位延迟对控制的影响,必要时进行延迟补偿。 |
| 仿真场景复现 (HIL/SIL) | 提供稳定、合理的车辆状态给仿真平台。 | 零相位滤波 (离线) 或 EKF (实时) | 离线分析用 filtfilt 消除相位延迟。确保虚拟传感器输入的合理性。 |
黄金法则:
- 目标驱动:先问"为什么滤波",再决定"怎么滤"。
- 保留原始数据:原始数据是"法律证据",永远不要丢弃。
- 透明公开:在报告中明确标注:滤波器类型、截止频率、阶数、是否零相位、实现库(如
scipy.signal)。- 验证对比:始终进行"滤波前后"对比,检查是否引入虚假特征或丢失关键信息。
结语:滤波器即哲学
滤波器的故事,远不止于数学公式。它体现了工程实践中最深刻的哲学——在噪声与真实、平滑与细节、效率与准确之间寻求平衡。
在自动驾驶这条充满不确定性的道路上,滤波器教会我们:真正的智能,不在于拥有完美的数据,而在于如何在不完美的世界中,做出最优的估计与决策。
当你下次看到一条平滑的车辆轨迹曲线时,请记住,那不仅是技术的胜利,更是无数工程师在"滤波"二字上反复权衡、严谨求证的结果。因为在这里,一个小小的截止频率,可能就决定了安全与危险的距离。
— by AGI 本文部分内容由通义千问生成整理汇总,仅供入门参考。欢迎学习交流!
参考文献
[1] Euro NCAP. (2022). Test Protocol Bulletin TB021: Data Acquisition and Injury Calculation (Version 4.1). Euro NCAP Technical Report. Retrieved from https://www.euroncap.com/media/79880/tb-021-data-acquisition-and-injury-calculation-v41.pdf
附录
文首的测试demo
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
from scipy.signal import butter, filtfiltdef butter_lowpass_filter(data, cutoff, fs, order=4):"""Apply Butterworth lowpass filterParameters:data : array_like - Input datacutoff : float - Cutoff frequency (Hz)fs : float - Sampling frequency (Hz)order : int - Filter orderReturns:y : array_like - Filtered data"""nyquist = 0.5 * fsnormal_cutoff = cutoff / nyquistb, a = butter(order, normal_cutoff, btype='low', analog=False)y = filtfilt(b, a, data)return y# Parameter settings
duration = 20 # Duration (seconds)
fs = 100 # Sampling frequency (Hz)
cutoff_freq_05 = 0.5 # Original cutoff frequency (Hz)
cutoff_freq_2 = 2.0 # New 2Hz cutoff frequency (Hz)
cutoff_freq_5 = 5.0 # New 5Hz cutoff frequency (Hz)
cutoff_freq_10 = 10.0 # New 10Hz cutoff frequency (Hz)
filter_order = 4 # Standard filter order
filter_order_12 = 4 # Standard filter order# Generate time axis
t = np.linspace(0, duration, int(fs * duration), endpoint=False)# Simulate lateral acceleration data (including multiple frequency components and noise)
# Low frequency components (real lateral acceleration changes)
true_acceleration = 2 * np.sin(2 * np.pi * 0.1 * t) + 1.5 * np.sin(2 * np.pi * 0.3 * t)# Additional components at 2Hz and 5Hz
additional_components = 0.8 * np.sin(2 * np.pi * 2 * t) + 0.6 * np.sin(2 * np.pi * 5 * t)# High frequency noise
noise = 0.5 * np.random.normal(0, 1, len(t)) + 0.3 * np.sin(2 * np.pi * 5 * t) + 0.2 * np.sin(2 * np.pi * 15 * t)# Original measurement data (real signal + additional components + noise)
raw_acceleration = true_acceleration + additional_components + noise# Apply Butterworth lowpass filters with different cutoff frequencies
filtered_acceleration_05 = butter_lowpass_filter(raw_acceleration, cutoff_freq_05, fs, filter_order)
filtered_acceleration_2 = butter_lowpass_filter(raw_acceleration, cutoff_freq_2, fs, filter_order)
filtered_acceleration_5 = butter_lowpass_filter(raw_acceleration, cutoff_freq_5, fs, filter_order)
filtered_acceleration_10 = butter_lowpass_filter(raw_acceleration, cutoff_freq_10, fs, filter_order_12)# Create separate plots for each filter
plt.figure(figsize=(15, 15))# Plot 1: Original data
plt.subplot(3, 3, 1)
plt.plot(t, raw_acceleration, 'b-', linewidth=0.8, label='Raw Data')
plt.xlabel('Time (s)')
plt.ylabel('Lateral Acceleration (m/s²)')
plt.title('Original Lateral Acceleration Data')
plt.grid(True, alpha=0.3)
plt.legend()# Plot 2: 0.5Hz filter
plt.subplot(3, 3, 2)
plt.plot(t, raw_acceleration, 'b-', linewidth=0.8, alpha=0.3, label='Raw Data')
plt.plot(t, filtered_acceleration_05, 'r-', linewidth=1.5,label=f'Butterworth LPF ({cutoff_freq_05} Hz, Order {filter_order})')
plt.xlabel('Time (s)')
plt.ylabel('Lateral Acceleration (m/s²)')
plt.title('0.5Hz Lowpass Filter')
plt.grid(True, alpha=0.3)
plt.legend()# Plot 3: 2Hz filter
plt.subplot(3, 3, 3)
plt.plot(t, raw_acceleration, 'b-', linewidth=0.8, alpha=0.3, label='Raw Data')
plt.plot(t, filtered_acceleration_2, 'g-', linewidth=1.5,label=f'Butterworth LPF ({cutoff_freq_2} Hz, Order {filter_order})')
plt.xlabel('Time (s)')
plt.ylabel('Lateral Acceleration (m/s²)')
plt.title('2Hz Lowpass Filter')
plt.grid(True, alpha=0.3)
plt.legend()# Plot 4: 5Hz filter
plt.subplot(3, 3, 4)
plt.plot(t, raw_acceleration, 'b-', linewidth=0.8, alpha=0.3, label='Raw Data')
plt.plot(t, filtered_acceleration_5, 'm-', linewidth=1.5,label=f'Butterworth LPF ({cutoff_freq_5} Hz, Order {filter_order})')
plt.xlabel('Time (s)')
plt.ylabel('Lateral Acceleration (m/s²)')
plt.title('5Hz Lowpass Filter')
plt.grid(True, alpha=0.3)
plt.legend()# Plot 5: 10Hz filter (12th order)
plt.subplot(3, 3, 5)
plt.plot(t, raw_acceleration, 'b-', linewidth=0.8, alpha=0.3, label='Raw Data')
plt.plot(t, filtered_acceleration_10, 'c-', linewidth=1.5,label=f'Butterworth LPF ({cutoff_freq_10} Hz, Order {filter_order_12})')
plt.xlabel('Time (s)')
plt.ylabel('Lateral Acceleration (m/s²)')
plt.title('10Hz Lowpass Filter (12th Order)')
plt.grid(True, alpha=0.3)
plt.legend()# Plot 6: Combined comparison of all filters
plt.subplot(3, 3, 6)
plt.plot(t, raw_acceleration, 'b-', linewidth=0.8, alpha=0.3, label='Raw Data')
plt.plot(t, filtered_acceleration_05, 'r-', linewidth=1.5,label=f'LPF ({cutoff_freq_05} Hz, Order {filter_order})')
plt.plot(t, filtered_acceleration_2, 'g-', linewidth=1.5,label=f'LPF ({cutoff_freq_2} Hz, Order {filter_order})')
plt.plot(t, filtered_acceleration_5, 'm-', linewidth=1.5,label=f'LPF ({cutoff_freq_5} Hz, Order {filter_order})')
plt.plot(t, filtered_acceleration_10, 'c-', linewidth=1.5,label=f'LPF ({cutoff_freq_10} Hz, Order {filter_order_12})')
plt.xlabel('Time (s)')
plt.ylabel('Lateral Acceleration (m/s²)')
plt.title('Combined View: All Filters Comparison')
plt.grid(True, alpha=0.3)
plt.legend()# 调整布局,增加上下部分之间的间距
plt.tight_layout(pad=3.0, h_pad=3.0, w_pad=1.0)
plt.show()# Print filter information
print(f"Sampling Frequency: {fs} Hz")
print(f"Standard Filter Order: {filter_order}")
print(f"10Hz Filter Order: {filter_order_12}")
print(f"Number of Data Points: {len(t)}")
print(f"Data Duration: {duration} s")
print("\nApplied Filters:")
print(f" - Lowpass Filter 1: {cutoff_freq_05} Hz (Order {filter_order})")
print(f" - Lowpass Filter 2: {cutoff_freq_2} Hz (Order {filter_order})")
print(f" - Lowpass Filter 3: {cutoff_freq_5} Hz (Order {filter_order})")
print(f" - Lowpass Filter 4: {cutoff_freq_10} Hz (Order {filter_order_12})")



















