目录
引言
一. 基本知识
二.参数估计
三.数据平滑
一.加1法
二.减值法/折扣法
编辑 1.Good-Turing 估计
编辑 2.Back-off (后备/后退)方法
3.绝对减值法
编辑4.线性减值法
5.比较
三.删除插值法(Deleted interpolation)
四.模型自适应
引言

本章节讲的知识主要是来解决以上这个问题:即如何计算一段话在我们日常生活中出现的概率。在学完本章节后,你可以尝试解决下面的问题:

一. 基本知识
对于一段话,我们如何计算其在生活中出现的概率呢?首先我们可以把每一句话拆分成一个个词,这些词就是我们所说的“统计基元”,一个个统计基元组成了我们的一句话。而对于我们每一个统计基元来说,其前面的基元就是历史基元。
如何计算一段话的概率?
假设我们这段话是“我爱你”,我们该怎么计算呢?你可能会想到,“我爱你”这句话的概率,不就应该等于“我”出现的概率*“爱”出现的概率*“你”出现的概率。实际上来说,这样算的话我们就忽略了词与词的关系,比如“爱”会不会影响“你”出现的概率,比如我们大部分人都会把“爱你”连起来说,这样的话我们就不能把他们俩独立开来了。这样的话,就相当于我们计算概率的时候要参考一句话前面的基元。因此我们应该用下面的公式:

可以理解为:句子的概率 = 第 1 个词的概率 × 第 2 个词依赖第 1 个词的概率 × 第 3 个词依赖前两个词的概率 × … × 第 m 个词依赖前 m - 1 个词的概率
历史基元数量爆炸问题
显然随着要预测的词位置越靠后(i 越大 ),需要参考的 “历史基元数量” 也越多(i−1 个 ),这样的话很容易出现后面的历史基元越来越多出现参数爆炸。即:

那我们该如何解决这个问题呢?
我们的解决办法是等价类划分:


举个例子:“我爱你”和“石头爱地”这两句话,假设n等于2,则“你”前面的“我爱”和“地”前面的“石头爱”,因为前n-1个基元,即“爱” 相同,则这俩句话为同一等价类。因此我们很容易看出来,这个n其实就是相当于缩减了我们的视野,我们只看前n-1个基元而看不到更前面的基元了。
因此:

但是,这样的话,显然我们的句子的第一个单词没有前置的选项让我们看了,也就是说没有历史基元,这对我们是非常不方便的,因为我们无法统一编程,并且我们还丢失了其作为第一个单词的位置信息。所以我们为这个句子加上了开头和结尾符号来标识。
即:
这样的话我们就非常好求解了,例题如下:

(下面三个分别是一元,二元,三元划分) 那么我们的概率就是:


二.参数估计
好了,既然我们已经整出来了表示,那么我们模型里的这些参数是啥呢?就是说我们这里的P是什么呢?这就引出了我们下面的概念:



例题:


那若是求一个句子里包含从没出现的词呢?这是很常见的,比如训练语料不可能包含所有人的姓名,如果一个人的姓名比较生僻,比如叫“诸葛大力”,这样的话是否“诸葛大力爱张伟”在日常生活中是不可能发生的呢?显然不是。但是我们的计算下整个的概率是0。显然是不合理的。于是我们便引出了数据平滑。
三.数据平滑


困惑度你就理解为这个句子的常见程度,如果困惑度很高,说明句子很罕见,让人看着很“困惑”。
一.加1法

意思就是分子加1,分母加上词汇库的总量(不包含开始和结束字符)
例题:

二.减值法/折扣法
 1.Good-Turing 估计
1.Good-Turing 估计


 举例:
举例:

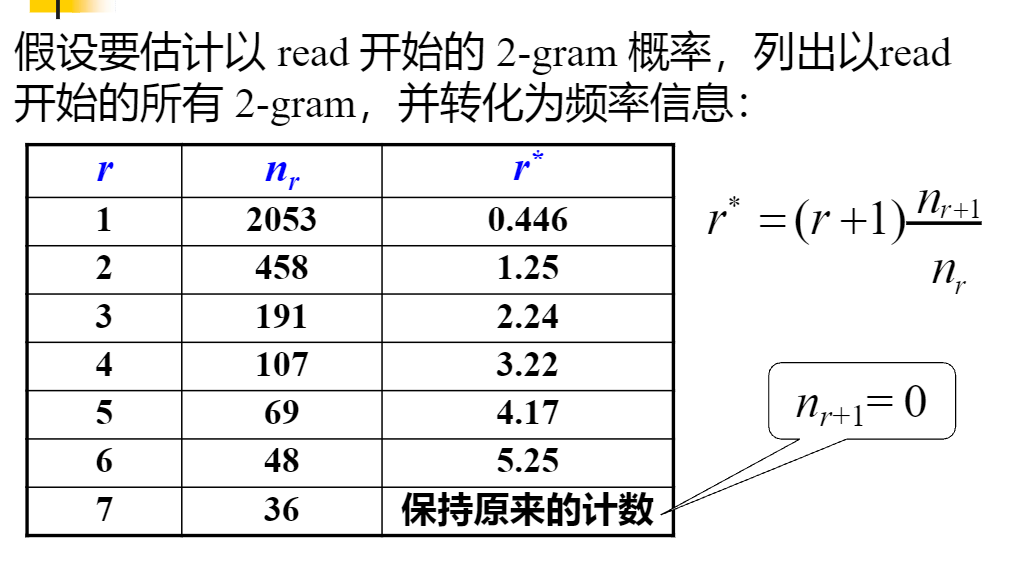 给你们算个一个吧。第一个r*,照着公式的话,r+1等于2,因为我们这里的r等于1,然后nr和nr+1直接看表的话就是2053和458,也就是说r*=2*(458/2053)约等于0.446,其他的你们照着我这样做就行。
给你们算个一个吧。第一个r*,照着公式的话,r+1等于2,因为我们这里的r等于1,然后nr和nr+1直接看表的话就是2053和458,也就是说r*=2*(458/2053)约等于0.446,其他的你们照着我这样做就行。


 2.Back-off (后备/后退)方法
2.Back-off (后备/后退)方法



3.绝对减值法
 4.线性减值法
4.线性减值法

5.比较

三.删除插值法(Deleted interpolation)


四.模型自适应












)
)






自动领积分脚本部署——基于python和Selenium(附源码))
—状态管理》)




