遇到一个挺有意思的题做个记录：
求曲线y = (x2+1)(x2−1)0.5\frac{\left(x^{2}+1\right)}{\left(x^{2}-1\right)^{0.5}}(x2−1)0.5(x2+1)渐近线的条数
比较明显的x = ±1是无定义点。但是在求极限的时候发现1+和1-得到的极限值似乎不一样。似乎是1+是趋向于+∞，1-趋向于-∞
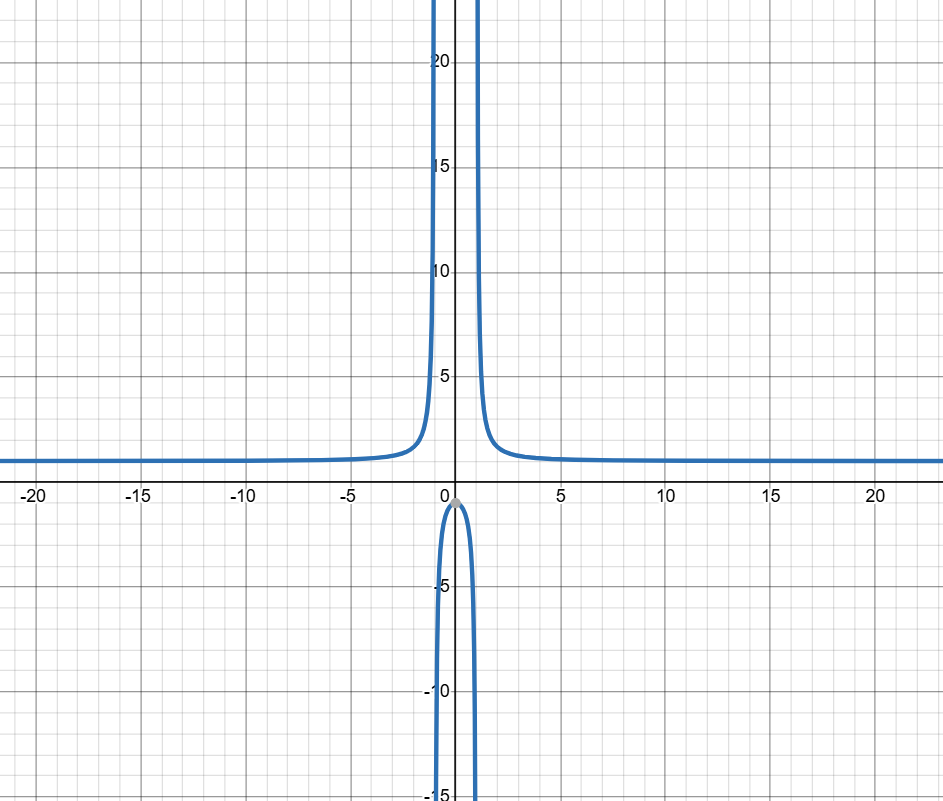
但是上述的理解是错误的，分母为根号，不存在复数开根号，负数部分应该直接舍去
只保留1+的部分，如下图
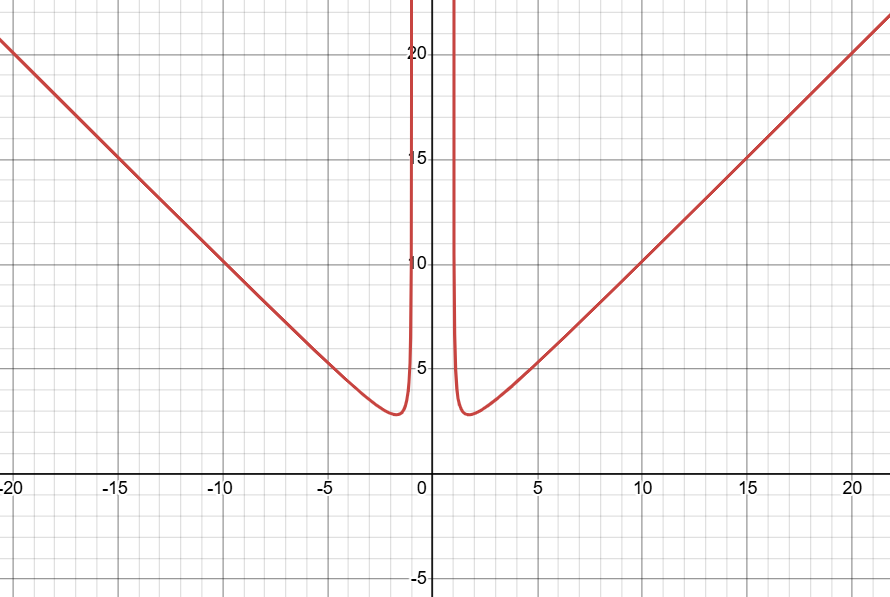
而图一所示适用于分母不开跟的情况
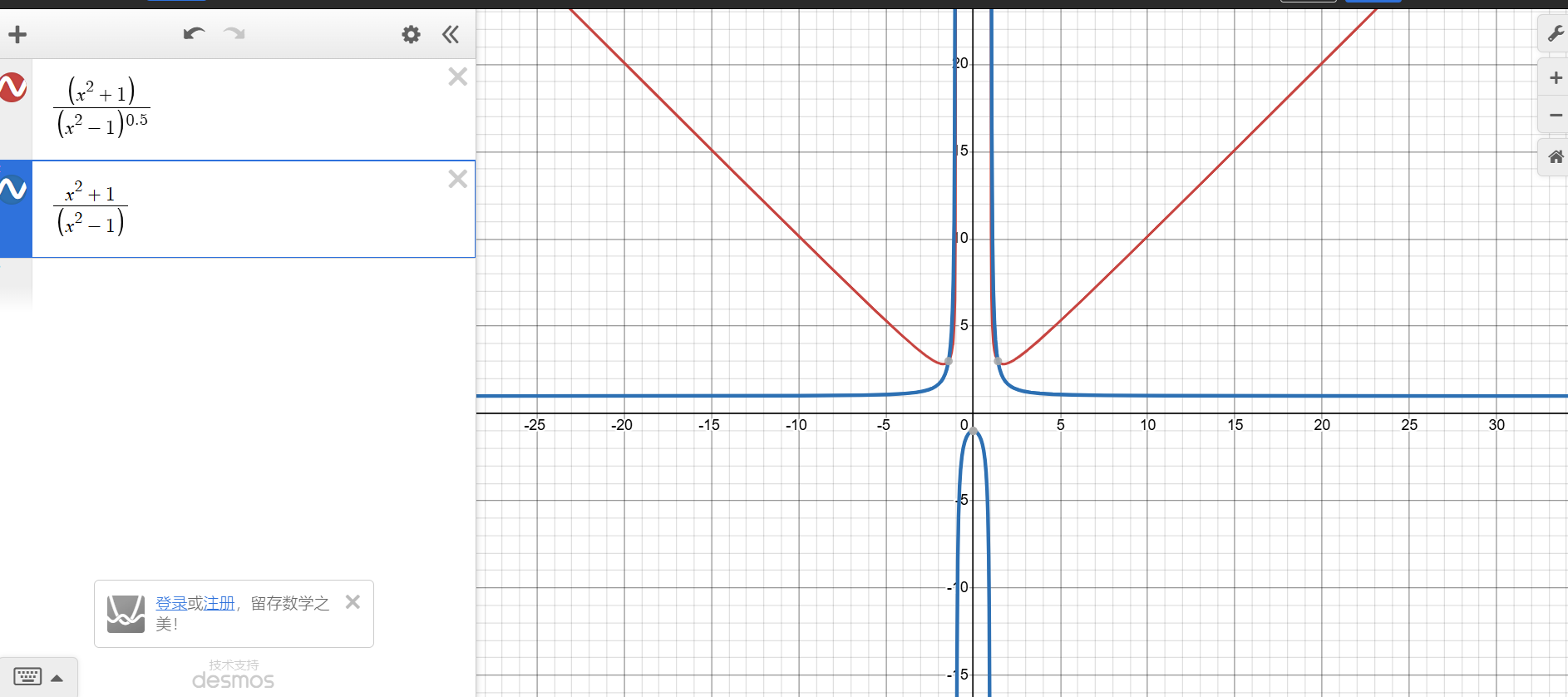
库pip下载超时、下载失败、无法下载的解决方案大全)
—语言模型+n元语法(1))
)
