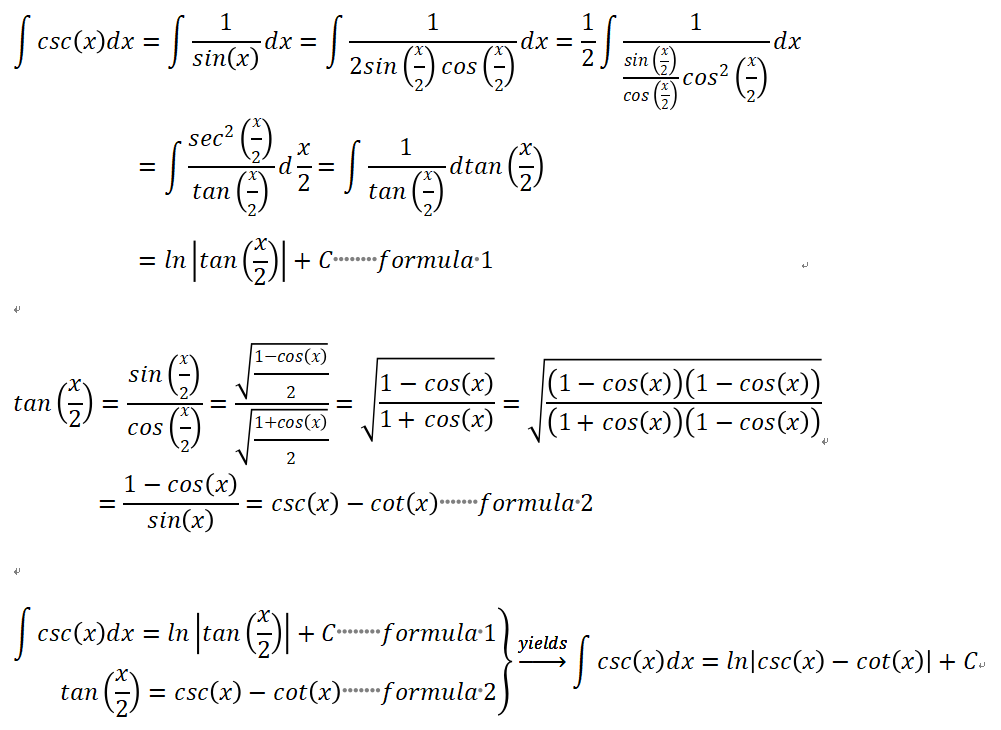
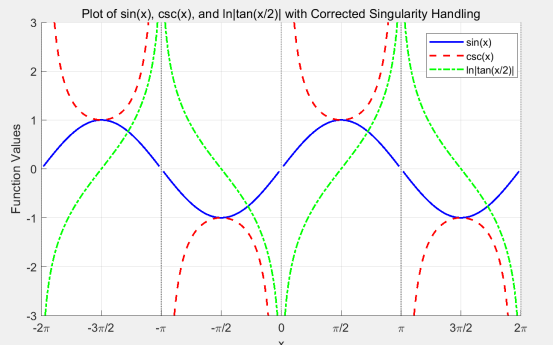
在MATLAB中同时绘制 sin⁡(x), csc(x) 和 ln⁡∣tan⁡(x/2)∣的函数图像，需要处理函数的奇点（如 csc⁡(x) 在 sin⁡(x)=0 时无定义，ln⁡∣tan⁡(x/2)∣ 在 x=kπ 时无定义）（deepseek生成matlab代码）

% 定义x范围（-2π到2π），高密度采样
x = linspace(-2*pi, 2*pi, 10000);% 精确识别csc(x)的奇点（sin(x)=0的点）
csc_singular_indices = find(abs(sin(x)) < 1e-3);  % 检测所有sin(x)接近0的位置% 创建奇点缓冲区（移除奇点附近±0.05弧度的点）
buffer_zone = 0.05;  % 缓冲区大小
for k = csc_singular_indicesstart_idx = max(1, k - floor(buffer_zone/(4*pi/10000)));end_idx = min(length(x), k + floor(buffer_zone/(4*pi/10000)));x(start_idx:end_idx) = NaN;
end% 计算函数值（使用处理后的x）
y_sin = sin(x);
y_csc = 1 ./ y_sin;  % csc(x) = 1/sin(x)% 处理ln|tan(x/2)|的奇点
y_tan_half = tan(x/2);
y_log = log(abs(y_tan_half));% 额外移除ln|tan(x/2)|的奇点（tan(x/2)无定义的位置）
log_singular = isnan(y_tan_half) | (abs(y_tan_half) < 1e-10);
x(log_singular) = NaN;
y_log(log_singular) = NaN;% 重新计算所有函数值
y_sin = sin(x);
y_csc = 1 ./ y_sin;
y_log = log(abs(tan(x/2)));% 创建图形窗口
figure;
hold on;% 绘制三条曲线
plot(x, y_sin, 'b-', 'LineWidth', 1.5);      % sin(x): 蓝色实线
plot(x, y_csc, 'r--', 'LineWidth', 1.5);     % csc(x): 红色虚线
plot(x, y_log, 'g-.', 'LineWidth', 1.5);     % ln|tan(x/2)|: 绿色点划线% 设置坐标轴范围和标签
xlim([-2*pi, 2*pi]);
ylim([-10, 10]);  % 限制Y轴范围
xlabel('x');
ylabel('Function Values');
title('Plot of sin(x), csc(x), and ln|tan(x/2)| with Corrected Singularity Handling');% 添加图例和网格
legend('sin(x)', 'csc(x)', 'ln|tan(x/2)|', 'Location', 'Best');
grid on;% 标记π倍数的刻度和奇点位置
xticks([-2*pi, -3*pi/2, -pi, -pi/2, 0, pi/2, pi, 3*pi/2, 2*pi]);
xticklabels({'-2\pi', '-3\pi/2', '-\pi', '-\pi/2', '0', ...'\pi/2', '\pi', '3\pi/2', '2\pi'});% 标记所有奇点位置（x = kπ）
singular_x = [-2*pi, -pi, 0, pi, 2*pi];
for k = 1:length(singular_x)line([singular_x(k) singular_x(k)], ylim, 'Color', [0.5 0.5 0.5], 'LineStyle', ':', 'LineWidth', 1);
end% 添加图例说明
text(-6, 9, 'Vertical asymptotes at x = kπ', 'Color', [0.5 0.5 0.5], 'FontSize', 10);hold off;