喜欢的话别忘了点赞、收藏加关注哦(关注即可查看全文),对接下来的教程有兴趣的可以关注专栏。谢谢喵!(=・ω・=)

4.3.1. 实战中会遇到的问题
首先看一个例子:
根据任检测数据x1x_1x1、x2x_2x2及其标签,判断x1=6x_1 = 6x1=6,x2=4x_2 = 4x2=4时所属的类别。
图像如下:
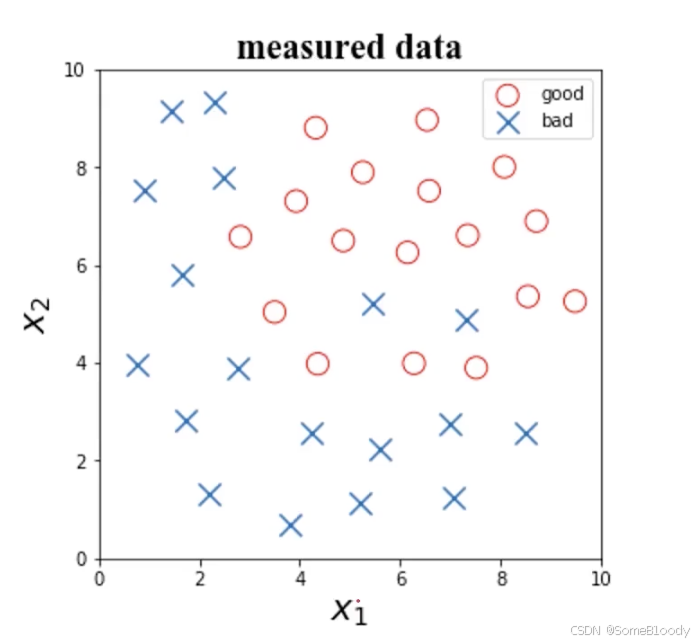
我们接下来就需要选择算法了,可选择的有:
- 逻辑回归(详见 1.6. 逻辑回归理论)
- KNN(详见 2.2. 聚类分析算法理论)
- 决策树(详见 3.1. 决策树理论)
- 神经网络(之后会讲)
选择完算法之后我们还会遇到一个问题:具体算法的核心结构/参数如何选择?
- 如果选择逻辑回归:边界函数用什么?用线性函数还是多项式?
- 如果选择KNN:核心参数
n_neighbors(指定的K值)取多少合适? - …
最后,如果模型表现不佳,具体表现为
- 训练数据准确率太低(欠拟合)
- 测试数据准确率下降明显(过拟合)
- 召回度/特异度/精确率低
这种情况下我该怎么办呢?
这些情况汇总下来就是一个问题:如何提高模型表现?
4.3.2. 数据决定上限
数据的质量决定了模型表现的上限。就算你用再强的模型/参数,只要你的数据质量差效果就好不起来。
建议在建模之前先检查数据的以下方面:
- 数据属性的意义,是否为无关数据
- 不同属性数据的数量级差异性如何
- 是否有异常数据
- 采集数据的方法是否合理,采集的数据是否有代表性
- 对于标签结果,要确保标签判定规则的一致性(统一标准)
| 对数据进行的操作 | 好处 |
|---|---|
| 删除不必要的属性 | 防止过拟合,节约运算时间 |
| 数据预处理:归一化、标准化 | 平衡数据影响,加快训练收敛 |
| 确定是否保留或过滤掉异常数据 | 提高实用性 |
| 尝试不同的模型,对比模型表现 | 帮助确定更合适的模型 |
以上文的例子来说,在我们获得数据之后,我们要考虑以下问题:
- 是否有需要剔除的异常数据?
- 数据量级差异如何?
- 是否需要降低数据维度?
对于检查异常数据这一部分,我们学过异常检测(详见 3.3. 异常检测(Anomaly Detection)理论),通过概率密度函数来找潜在的数据异常点。
对于数据量级差异的部分,我们要先看数据的分布,x1x_1x1的数据分布在0.77~9.49,x2x_2x2的数据分布在0.69~9.5。这两个变量的数据分布基本相同,可以不做归一化处理。
对于确认是否需要降低数据维度的部分,我们需要先对数据进行主成分分析(详见 3.4. 主成分分析(PCA)理论)。由于例子中的数据只有2个维度,所以就不需要进行主成分分析来降维了,具体的操作见 3.7. 主成分分析(PCA)实战。
4.3.3. 尝试不同的模型
不同的模型通常会有不同的效果,你可以计算准确率并可视化出来,这里的数据使用的是 1.9. 逻辑回归实战 中的,我把.csv数据文件放在GitCode上了,点击链接即可下载。
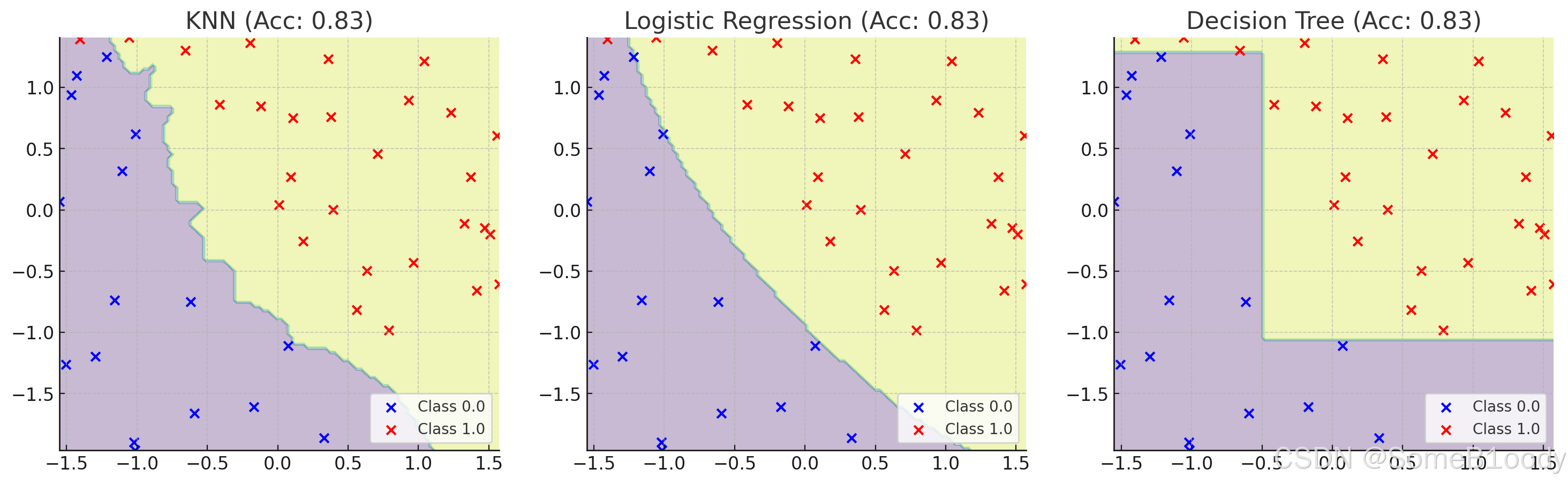
你也可以通过混淆矩阵来计算其它参数,根据其他指数来决定要使用哪个模型。衡量指标的选择取决于应用场景:
- 垃圾邮件检测(正样本为“垃圾邮件“):希望普通邮件(负样本)不要被判断为垃圾邮件(正样本),即:判断为垃圾邮件的样本都是判断正确的,需要关注精确率;还希望所有的垃圾邮件尽可能被判断出来,需要关注召回率。
- 异常交易检测(正样本为“异常交易”):希望判断为正常的交易(负样本)中尽可能不存在异常交易,还需要关注特异度。
4.3.4. 其他调整
在确定了该使用什么模型之后,我们还需要对其他方面进行微调:
- 遍历核心参数组合,评估对应模型表现(比如:逻辑回归边界函数考虑多项式、KNN尝试不同的
n_neighbors值) - 扩大数据样本
- 增加或减少数据属性
- 对数据进行降维处理(主成分分析PCA)
- 对模型进行正则化处理,调整正则项λ\lambdaλ的数值(详见 4.1. 过拟合(overfitting)与欠拟合(underfitting) )
来看看KNN的n_neighbors值对结果的影响:
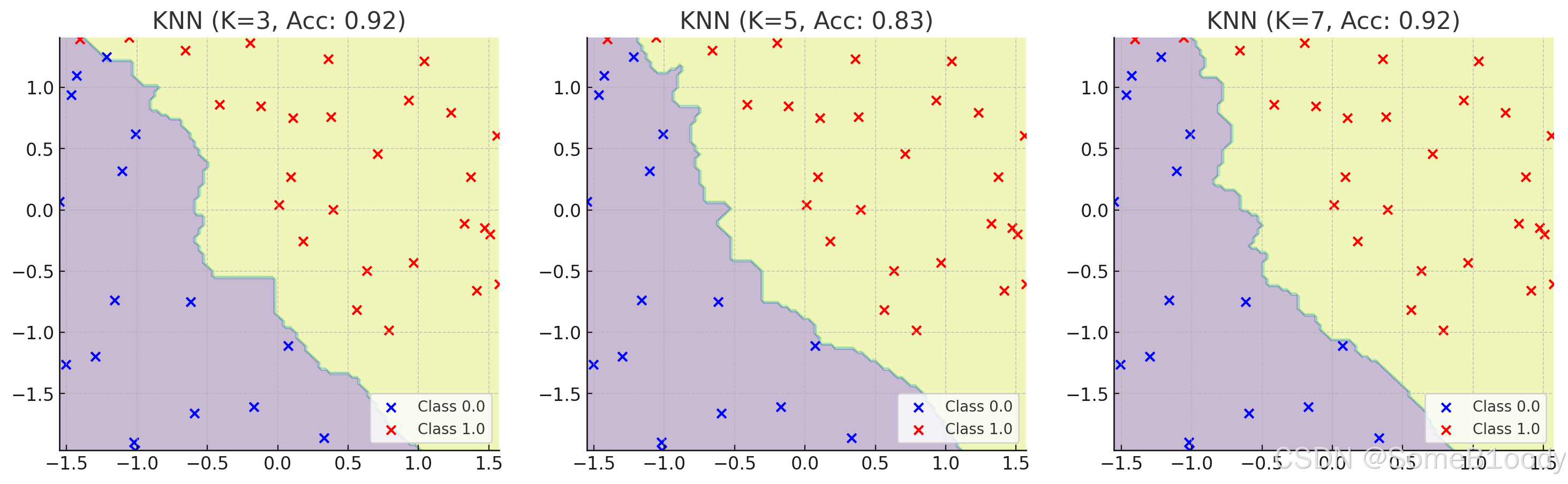
)








![uniapp “requestPayment:fail [payment支付宝:62009]未知错误“](http://pic.xiahunao.cn/uniapp “requestPayment:fail [payment支付宝:62009]未知错误“)
的带状细胞对NLP中的深层语义分析的积极影响和启示)
)
)






