ConvMixer模型：纯卷积为何能够媲美Transformer架构？深入浅出原理与Pytorch代码逐行讲解实现

ConvMixer 是一个简洁的视觉模型，仅使用标准的卷积层，达到与基于自注意力机制的视觉 Transformer（ViT）相似的性能，由此证明纯卷积架构依然很强大。

核心原理：极简的卷积设计：

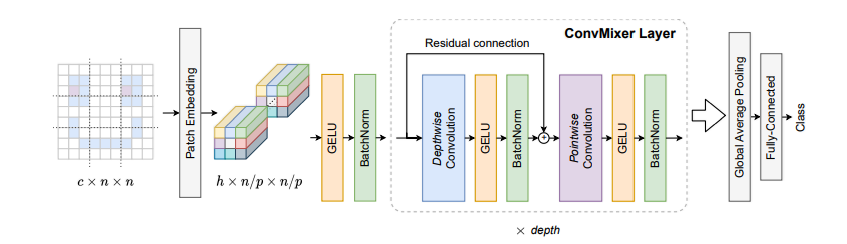
它摒弃了复杂的自注意力模块，只依赖于两种基础的卷积操作：深度卷积（Depthwise Convolution） 和逐点卷积（Pointwise Convolution）。

制作一杯混合果汁。我们不会把整个水果直接扔进搅拌机，而是先切成小块（分块）。然后，搅拌机有两个关键动作：第一，刀片高速旋转，让每种水果块自己先碎掉（空间混合）；第二，整个杯子里的碎块因为搅动而互相融合在一起（通道混合）。

ConvMixer 的设计与此相似。它认为，复杂的图像特征提取，可以被分解为这两个最基本、最核心的“搅拌”动作，而不需要像 Vision Transformer 那样引入复杂的自注意力机制。

我们来一步步看这个模型是如何工作的。

1. 分块嵌入 (Patch Embedding)：

传统卷积的起点：

传统的卷积网络（如 VGG）通常在开头使用小的卷积核（比如 3x3），步长为1或2。这意味着网络一开始的视野非常小，它是在逐个像素地、非常局部地观察图像。它需要堆叠很多层，才能慢慢地将局部信息组合起来，形成对一个更大区域的理解。

ConvMixer 的革新：

ConvMixer 借鉴了 Vision Transformer (ViT) 的一个核心思想：不要一开始就纠结于像素细节，而是直接把图像切成一块块（Patches），把每一块作为一个基本处理单元。

它如何用卷积实现这一点呢？请看代码：

nn.Conv2d(in_channels=3, out_channels=dim, kernel_size=7, stride=7)
#当卷积核的大小和移动步长相同时，效果就是卷积核在图像上进行不重叠的滑动。
#每滑动一次，这个 7x7 的卷积核就完整地覆盖了一个 7x7 的图像块（Patch）。
#它将这个块内的所有像素信息（3个通道的 7x7=49 个像素）进行一次计算，然后“压缩”成 dim 个通道的 一个 像素点。

这一步的意义：

降维与提炼：瞬间将高分辨率的图像（如 224x224x3）转换成一个低分辨率的特征图（如 32x32x768）。这大大减少了后续计算量。
视角转变：强迫模型从一开始就从一个“区域”（Patch）的层面去理解图像，而不是从单个像素。这与人类的视觉习惯更相似，我们看一张图也是先看整体布局和各个区域，再看细节。
信息嵌入：out_channels=dim 这个参数（例如 dim=768）意味着每个图像块被转换成了一个包含 768 个特征的向量。这个过程被称为“嵌入”（Embedding），它将原始的像素信息转化成了更利于模型处理的、高维的抽象特征

2. ConvMixer 层：

这是模型的核心，它由 深度卷积 (Depthwise Convolution) 和 逐点卷积 (Pointwise Convolution) 构成。这种组合也被称为 深度可分离卷积 (Depthwise Separable Convolution)，是 MobileNet 等轻量级网络的基石。

深度卷积 (Depthwise Conv)：空间混合

经过分块嵌入后，我们得到了一个 dim 通道（比如 768 个通道）的特征图。每个通道都可以看作是图像在某个特定方面的特征表达（比如某个通道可能对轮廓敏感，另一个对纹理敏感）。一个 9x9 的普通卷积核，在计算输出特征图的一个点时，会同时查看输入特征图上 9x9 区域内的所有 768 个通道的信息，然后把它们加权求和。这是“空间混合”和“通道混合”同时进行的，计算开销巨大。

深度卷积却将这两个过程分离开。深度卷积只负责空间混合。

具体过程：

一个通道，一个专属卷积核：如果输入有 C 个通道，深度卷积就会使用 C 个扁平的（2D）卷积核（例如 3x3x1）。
独立工作：第1个卷积核只负责在第1个输入通道上滑动，第2个卷积核只负责第2个通道……以此类推。
保持通道数：处理完成后，输出的通道数仍然是 C。它只在每个通道内部进行了空间特征提取，但通道之间还是完全隔离的。

核心目的：用极低的计算成本，在每个特征通道内部有效地捕捉空间模式。

逐点卷积 (Pointwise Convolution)：通道混合：

深度卷积完成了空间特征整理，但留下了致命问题：通道之间完全没有信息交流。这就像一个公司里，销售、技术、市场三个部门都各自完成了自己的KPI，但他们之间从不开会，公司无法形成合力。逐点卷积就是来主持这场“跨部门会议”的。它只专注于第二步：通道混合。它的工作方式非常简单，就是一次 1x1 的卷积。

具体过程：

微型卷积核：它的卷积核大小是 1x1。这意味着它在空间上看的范围只有一个像素点，所以它完全不做空间混合。
贯穿所有通道：这个 1x1 的卷积核是立体的（例如 1x1xC，C是深度卷积的输出通道数，；比如768个通道）。在特征图的每一个像素点上，它都会同时考虑所有 768个通道的值，然后进行加权求和，输出一个新值。
重组特征：通过使用 N 个这样的 1x1xC 卷积核，它就可以将输入的 C 个通道的信息，重新组合成 N 个全新的、更有意义的特征通道。

核心目的：在不同通道之间建立联系，让模型学习如何将从不同通道提取出的空间特征（比如“有笔直的轮廓”、“有红色的纹理”）组合成更高级的概念（比如“这是一支笔”）。

当深度卷积和逐点卷积按顺序组合在一起时，就构成了大名鼎鼎的深度可分离卷积。

流程：输入 -> 深度卷积 (空间混合) -> 逐点卷积 (通道混合) -> 输出

这个结构可以成功的原因来自于它背后的假设：空间相关性（一个区域内的像素关系）和通道相关性（不同特征之间的关系）是可以被分开处理的，事实证明，这种解耦思想很成功。

3. 数据参数对比：

假设我们有如下任务：

输入特征图: 16x16x256 (高 x 宽 x 通道数)
输出特征图: 16x16x512
卷积核大小: 3x3

方案一：标准卷积

需要 512 个 3x3x256 的立体卷积核。
总参数量 = 3×3×256×512=1,179,648

方案二：深度可分离卷积

深度卷积 (空间混合):
- 需要 256 个 3x3x1 的扁平卷积核。
- 参数量 = 3×3×256=2,304
- 得到一个 16x16x256 的中间特征图。
逐点卷积 (通道混合):
- 需要 512 个 1x1x256 的卷积核，将 256 通道变为 512 通道。
- 参数量 = 1×1×256×512=131,072

总参数量 = 2,304+131,072=133,376

结果对比：标准卷积需要约 118 万 参数，而深度可分离卷积只需要约 13 万 参数，参数量减少到了原来的 11% 左右！

这就是为什么深度可分离卷积成为了 MobileNet、Xception、ConvMixer 等高效模型的基石。它用极低的成本，实现了与标准卷积非常接近的特征提取能力。

4. Pytorch代码逐行讲解实现:

我们回顾一下结构：

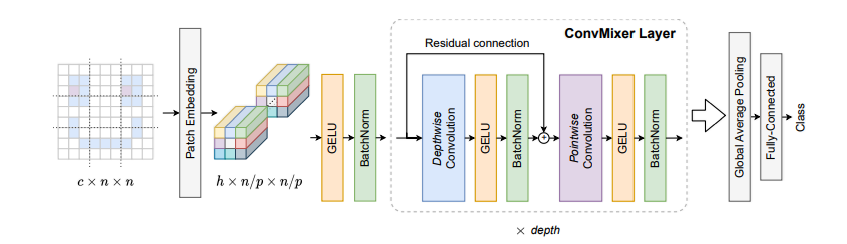
1. 核心组件：`ConvMixerLayer`

我们先构建模型最小、也是最核心的重复单元——ConvMixerLayer。它包含了我们详细讨论过的 深度卷积、逐点卷积 和 残差连接。

import torch
import torch.nn as nnclass ConvMixerLayer(nn.Module):"""ConvMixer 的核心重复层。包含一个深度卷积和一个逐点卷积，并通过残差连接。"""def __init__(self, dim, kernel_size=9):# 初始化 PyTorch 模块super().__init__()# --- 定义层的各个组件 ---# 1. 深度卷积 (Depthwise Convolution)#    负责在每个通道内部进行空间信息混合。self.depthwise_conv = nn.Conv2d(dim,                      # 输入通道数。dim,                      # 输出通道数与输入相同。kernel_size=kernel_size,  # 使用一个较大的卷积核（如9x9）来获取大感受野。groups=dim,               # 分组数=通道数，这是实现“深度卷积”的关键技巧。padding="same"            # 'same' 填充可以确保卷积后特征图的高和宽不变。)# 2. 激活函数 (Activation)#    为模型引入非线性，GELU 是 Transformer 中常用激活函数。self.activation = nn.GELU()# 3. 批归一化 (Batch Normalization)#    在网络层之间稳定和加速训练。self.norm = nn.BatchNorm2d(dim)# 4. 逐点卷积 (Pointwise Convolution)#    负责在通道之间混合信息，它本质上就是一个 1x1 的标准卷积。self.pointwise_conv = nn.Conv2d(dim,                      # 输入通道数。dim,                      # 输出通道数。kernel_size=1             # **核大小为1x1，是实现“逐点卷积”的关键**。)def forward(self, x):# 定义数据如何“流过”这个层 (前向传播)# 输入 x 的维度: [批次大小, 通道数, 高, 宽]# 1. 保存原始输入，用于最后的残差连接residual = x# 2. 应用第一个处理块：深度卷积 -> 激活 -> 归一化x = self.depthwise_conv(x)x = self.activation(x)x = self.norm(x)# 3. 应用第二个处理块：逐点卷积 -> 激活 -> 归一化x = self.pointwise_conv(x)x = self.activation(x)x = self.norm(x)# 4. 完成残差连接return x + residual

2. 整体架构：`ConvMixer` 模型

现在，我们把 ConvMixerLayer 堆叠起来，并加上开头的“分块嵌入”和结尾的“分类头”，构成完整的 ConvMixer 模型。

class ConvMixer(nn.Module):"""完整的 ConvMixer 模型架构。"""def __init__(self, dim, depth, kernel_size=9, patch_size=7, num_classes=1000):super().__init__()# --- 1. 分块嵌入 (Patch Embedding) ---# 使用一个卷积层同时实现图像分块和特征嵌入。self.patch_embedding = nn.Sequential(nn.Conv2d(3,                        # 输入是RGB图像，所以有3个通道。dim,                      # 输出通道数，即我们想要的嵌入维度。kernel_size=patch_size,   # 卷积核大小等于块大小。stride=patch_size         # 步长等于核大小，确保分块不重叠。),nn.GELU(),                    # 同样使用 GELU 激活函数。nn.BatchNorm2d(dim)           # 批归一化。)# --- 2. 堆叠 ConvMixer 层 ---self.mixer_layers = nn.Sequential(*[ConvMixerLayer(dim=dim, kernel_size=kernel_size) for _ in range(depth)])# --- 3. 分类头 (Classification Head) ---# a. 全局平均池化#    将每个通道的 HxW 特征图压缩成一个 1x1 的值。self.global_avg_pool = nn.AdaptiveAvgPool2d((1, 1))# b. 全连接层 (分类器)#    将池化后的向量映射到最终的类别数量上。self.classifier = nn.Linear(dim, num_classes)def forward(self, x):# 定义数据在整个模型中的流动路径# 初始输入 x 维度: [批次大小, 3, 224, 224] (以ImageNet为例)# 1. 应用分块嵌入#    x 维度变为 -> [批次大小, dim, 32, 32] (224 / 7 = 32)x = self.patch_embedding(x)# 2. 通过所有 ConvMixer 层#    维度保持不变 -> [批次大小, dim, 32, 32]x = self.mixer_layers(x)# 3. 应用全局平均池化#    x 维度变为 -> [批次大小, dim, 1, 1]x = self.global_avg_pool(x)# 4. 展平张量以适应全连接层#    `torch.flatten(x, 1)` 会将从第1个维度（通道维）开始的所有维度拍平。#    x 维度变为 -> [批次大小, dim]x = torch.flatten(x, 1)# 5. 通过分类器得到最终输出#    x 维度变为 -> [批次大小, num_classes]return self.classifier(x)

3. 实例化与测试

最后，让我们创建模型的一个实例，并用一个假的图像数据来测试它，看看整个流程是否能跑通。

# --- 实例化一个 ConvMixer-1536/20 模型 ---
# 这是论文中提出的一个高性能版本配置
# dim=1536, depth=20, kernel_size=9, patch_size=7
model = ConvMixer(dim=1536,depth=20,kernel_size=9,patch_size=7,num_classes=1000  # ImageNet 数据集的类别数
)# 打印模型结构，可以清晰地看到我们定义的每一层
# print(model)# --- 创建一个假的输入图像张量进行测试 ---
# 模拟一个批次包含4张 224x224 的3通道彩色图像
dummy_images = torch.randn(4, 3, 224, 224)# 将假图像输入模型，得到输出
output = model(dummy_images)# 打印输出张量的形状
# 预期输出: torch.Size([4, 1000])，代表每张图片都得到了1000个类别的得分
print(f"输入张量形状: {dummy_images.shape}")
print(f"输出张量形状: {output.shape}")

OK，结束，希望可以帮助大家学会这个轻量化模型。