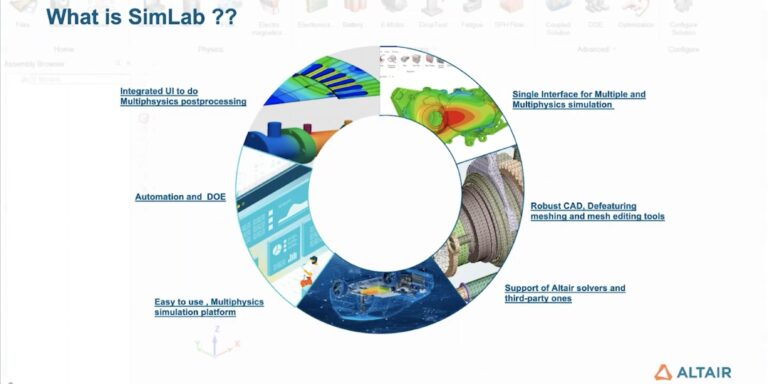
半导体行业正快速超越传统2D封装技术,积极采用 3D集成电路(3D ICs)和2.5D 先进封装等方案。这些技术通过异构芯粒、硅中介层和复杂多层布线实现更高性能与集成度。然而,由于电子计算机辅助设计(ECAD)数据规模庞大且结构复杂,这种技术演进给建模、仿真和可靠性评估带来了重大挑战。
01、现代 ECAD 模型日益增长的复杂性
现代 IC 封装在多层布线中涉及数千条网络,并采用多种具有不同物理特性的材料,导致 ECAD 数据集极为庞大,难以管理与分析。3D 存储立方体和堆叠芯片封装中的高密度布线及紧凑布局,还带来了更高的功率密度和机械应力。设计人员面临热应力、分层、芯片翘曲和焊料疲劳等问题,这些都可能严重影响封装的可靠性。传统仿真工具难以高效处理此类精细模型,往往需要过长的运行时间,限制了早期设计探索的空间。
02、多物理场仿真面临的挑战
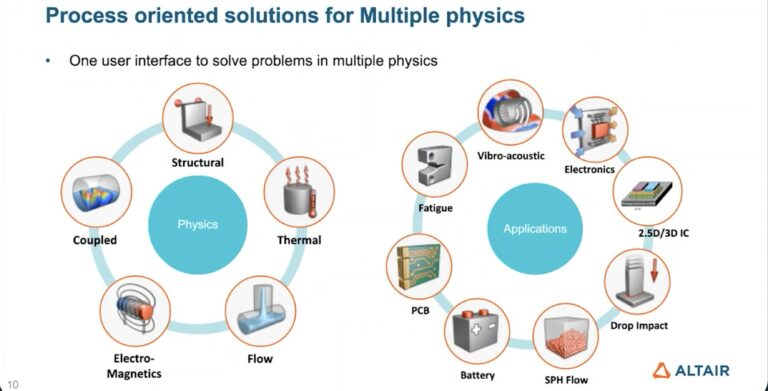
大规模 3D IC 封装的多物理场仿真存在多重技术难点。首先,ECAD 数据的体量和复杂性对现有工具的模型导入与处理能力形成巨大压力。精确分析需要耦合热、机械、疲劳和电磁等多重物理效应,同时还需处理异质材料和薄层几何结构。尽管全局精细网格划分会带来高昂的计算成本,但在关键区域仍不可或缺。此外,向系统级布局规划和异质集成的转型,也要求传统 EDA 工具尚未完全支持的新型工作流程。
03、Altair SimLab 的突破性解决方案
Altair SimLab 通过专为大规模 ECAD 模型设计的革命性多物理场仿真环境,有效应对上述挑战。该解决方案具备以下创新特性:
1.高效模型处理能力
将模型导入时间从数小时缩短至分钟级,使常规桌面硬件即可完成精细仿真。
2.智能金属映射技术
基于金属与介电质的体积含量计算等效材料属性,将精密布线结构简化为有效的连续材料表征,同时保持仿真精度。
3.混合建模体系
采用差异化建模方法:
信号层处理为壳单元
过孔简化为梁单元
绝缘层建模为实体单元
这种分层表示方式支持灵活的网格划分策略
04、SimLab 的进阶仿真能力
SimLab 通过创新的子模型技术进一步完善仿真流程,为设计人员提供高效精准的分析方案:
1.智能子模型分析
支持快速全局仿真结合迹线映射技术,精准定位需要详细分析的关键区域
自动将位移等边界条件从全局模型传递至局部子模型,实现速度与精度的最优平衡
2.多物理场集成环境
在统一界面中集成热分析、热应力分析、焊料疲劳分析和封装可靠性分析
提供从热力学到机械可靠性的完整解决方案
3.开放式求解架构
兼容第三方求解器接口
可扩展的多物理场分析能力
为先进封装提供端到端的分析支持
05、Altair SimLab 如何赋能工程师创新
通过整合三大核心技术优势,Altair SimLab 显著提升工程仿真效率与精度:
1.全流程效率提升
可扩展的模型导入技术
灵活的混合建模方法
智能多物理场耦合分析
将仿真周期缩短达80%,预测准确率提升30%+
2.早期设计探索能力
支持在设计初期快速评估:
✓ 不同工艺节点的可行性
✓ 多种封装配置方案
✓ 各类"假设分析"场景
帮助团队基于数据驱动做出关键决策
3.可靠性验证革新
实现关键结构的精细化分析:
焊球(solder bumps)疲劳寿命预测
过孔(vias)应力分布评估
互连(interconnects)可靠性验证
提前识别90%以上的潜在失效风险。
4.商业价值创造
✓ 减少50%以上的设计返工
✓ 缩短40%产品开发周期
✓ 提升最终产品良率15-20%
06、Altair SimLab如何助力工程师
通过整合可扩展的模型导入、灵活的建模方法和多物理场耦合技术,Altair SimLab 使工程师能够加速仿真流程并提升预测精度。设计人员可在设计周期早期快速探索"假设分析"场景,从而就工艺节点和封装配置做出更明智的决策。高效的数据处理能力支持对焊球、过孔和互连结构进行详细的可靠性分析,有助于在制造前识别潜在故障点。这种方法减少了昂贵的重新设计,缩短了开发周期,最终产出更可靠的半导体产品。
07、案例结果:显著节省时间
Altair SimLab 的强大性能在实际测试案例中得到充分验证。某42cm×34cm的大型PCB案例显示,该板卡包含14个布线层和7500多条网络。SimLab将模型导入时间从高性能计算系统所需的4个多小时缩短至普通笔记本电脑仅需5分钟。另一66mm×66mm硅中介层案例中,12个布线层和3000多条网络的导入时间从1小时缩减至3分钟。这些结果充分证明,Altair高效的 ECAD 数据处理能力使得复杂多物理场仿真能够在常规硬件上快速且经济地完成。
08、总结
随着半导体封装技术持续向3D IC和异质集成方向发展,仿真工具必须跟上日益增长的复杂度挑战。Altair SimLab 提供了一个可扩展的集成平台,有效弥合海量ECAD 数据与精确多物理场分析之间的鸿沟。其创新的建模技术和高效的工作流程赋能设计人员加速创新、优化可靠性,并从容应对先进封装技术的各项挑战。通过革新大规模 ECAD 模型的导入与分析方式,Altair SimLab 在推动新一代半导体设备发展方面发挥着关键作用。
申请免费试用
如您对 Altair 软件及解决方案感兴趣
欢迎关注Altair,申请免费试用
Altair 是计算智能领域的全球指引者之一,在仿真、高性能计算 (HPC) 和人工智能等领域提供软件和云解决方案,服务于16000多家全球企业,应用行业包括汽车、消费电子、航空航天、能源、机车车辆、造船、国防军工、金融、零售等。
近期,Altair被全球工业软件指引者西门子收购,成为西门子数字化工业软件(Siemens Digital Industries Software)旗下成员,进一步巩固西门子在仿真和工业人工智能领域的全球领导者地位,其技术正与西门子Xcelerator解决方案进行深度整合。
更多内容欢迎关注 AltairChina


)
















