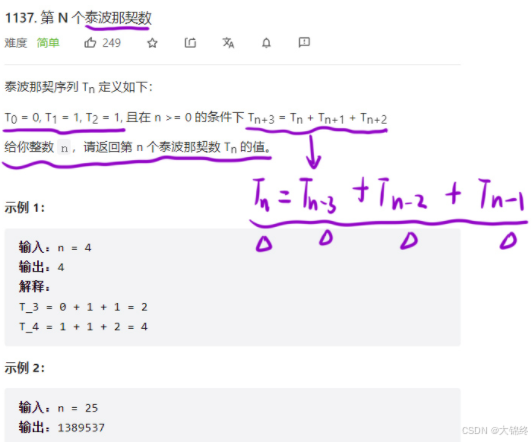
一. (1137.)第N个泰波那契数(力扣)
1.1动态规划的算法流程
对于初学者来讲学术上的概念晦涩难懂,将用通俗易懂的方式带来感性的理解.
1.状态表示
dp表(一维或二维数组)里面的值所表示的含义
从哪获取?
1.题目要求,如本题
2.题目没有明确说明的情况下+做题经验的累积
3.分析问题的过程中,发现重复的子问题来概括
2.状态转移方程
就是dp表元素等于什么,是一种递推关系式,本题已告知
3.初始化
要确保填dp表时不越界,对填表时越界的元素首先初始化
4.填表顺序
为了填写当前状态的时候,所需要的状态已经计算过了的顺序,本题为从左向右
5.返回值
取决于题目要求+状态表示,本题为第n个数的值
class Solution {
public:int tribonacci(int n) {//处理边界情况if(n==0) return 0;if(n==1||n==2) return 1;vector<int> dp(n+1);dp[0]=0,dp[1]=1,dp[2]=1;for(int i=3;i<=n;i++){dp[i]=dp[i-1]+dp[i-2]+dp[i-3];}return dp[n];}
};
6.空间优化
只会在本系列和背包问题中出现并分析,为了降低空间复杂度,能将一个级别
分析本题:滚动数组法
常规做法通过创建一个dp表数组来计算并存储结果,但是通过递推关系式得知想得到当前数的值只需要知道前面三个元素的值即可,那么另外不需要的空间就相当于浪费,所以可以考虑用四个变量来记录,每次更新后三个变量来进行下一次计算,如此循环往复
要注意更新变量的数据顺序问题,避免被覆盖
做法1:
class Solution {
public:int tribonacci(int n) {//处理边界情况if(n==0) return 0;if(n==1||n==2) return 1;//优化int k=3;//初始计算次数,从第三次开始计算int a=0,b=1,c=1,d=0;while(k<=n)//判断计算次数,返回条件{d=a+b+c;//更新变量a=b,b=c,c=d;k++;}return d;}
};做法2(不用控制计算次数):
class Solution {
public:int tribonacci(int n) {if(n == 0) return 0;if(n == 1 || n == 2) return 1;int a = 0, b = 1, c = 1, d = 0;for(int i = 3; i <= n; i++){d = a + b + c;a = b; b = c; c = d;}return d;}};
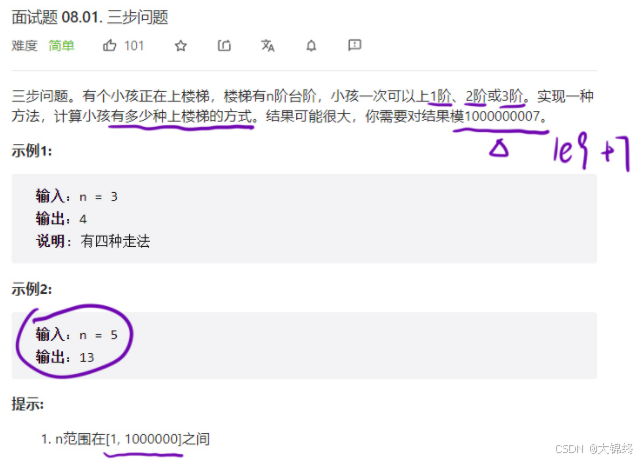
二. ⾯试题 08.01. 三步问题(力扣)
2.1算法原理
- 状态表⽰
这道题可以根据「经验 + 题⽬要求」直接定义出状态表⽰:
dp[i] 表⽰:到达 i 位置时,⼀共有多少种⽅法。
- 状态转移⽅程
以 i 位置状态的最近的⼀步,来分情况讨论:
如果 dp[i] 表⽰⼩孩上第 i 阶楼梯的所有⽅式,那么它应该等于所有上⼀步的⽅式之和:(一次最多上三级台阶)
i. 上⼀步上⼀级台阶, dp[i] += dp[i - 1] ;
ii. 上⼀步上两级台阶, dp[i] += dp[i - 2] ;
iii. 上⼀步上三级台阶, dp[i] += dp[i - 3] ;
综上所述, dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3] 。
需要注意的是,这道题⽬说,由于结果可能很⼤,需要对结果取模。在计算的时候,三个值全部加起来再取模,即 (dp[i - 1] + dp[i - 2] + dp[i - 3]) %MOD 是不可取的, n 取题⽬范围内最⼤值时,⽹站会报错 signed integer overflow 。
对于这类需要取模的问题,我们每计算⼀次(两个数相加/乘等),都需要取⼀次模。否则,万⼀发⽣了溢出,答案就错了
- 初始化
从我们的递推公式可以看出, dp[i] 在 i = 0, i = 1 以及 i = 2 的时候是没有办法进⾏推导的,因为 dp[-3] dp[-2] 或 dp[-1] 不是⼀个有效的数据。因此我们需要在填表之前,将 0,1, 2位置的值初始化。根据题意,, dp[0] = 1, dp[1] = 1, dp[2] = 2。
- 填表顺序
爬台阶从下往上,对应数组从左往右,毫⽆疑问是「从左往右」。
- 返回值
应该返回 dp[n] 的值。
class Solution {
public:int waysToStep(int n) {//判断边界情况if(n==0|n==1) return 1;if(n==2) return 2;vector<int> dp(n+1);//初始化dp[0]=1,dp[1]=1,dp[2]=2;for(int i=3;i<=n;i++){//取模操作防止数据溢出dp[i]=((dp[i-1]+dp[i-2])%1000000007+dp[i-3])%1000000007;}return dp[n];}
};
三. (746.) 使⽤最⼩花费爬楼梯(力扣)

注意:数组内的每⼀个下标 [0, n - 1] 表⽰的都是楼层,⽽顶楼的位置其实是在 n 的位置!
3.1算法原理
解法1
1.状态表示
dp[i] 表⽰:到达 i 位置时的最⼩花费。(注意:到达 i 位置的时候, i 位置的钱不需要算上)
2.状态转移方程
根据最近的⼀步,分情况讨论:
▪ 先到达 i - 1 的位置,然后⽀付 cost[i - 1] ,接下来⾛⼀步⾛到 i 位置:dp[i - 1] + csot[i - 1]
▪ 先到达 i - 2 的位置,然后⽀付 cost[i - 2] ,接下来⾛⼀步⾛到 i 位置:dp[i - 2] + csot[i - 2]
- 初始化:
从递推公式可以看出,需要先初始化 i = 0 ,以及 i = 1 位置的值。容易得到dp[0] = dp[1] = 0 ,因为不需要任何花费,就可以直接站在第 0 层和第 1 层上
- 填表顺序:
根据「状态转移⽅程」可得,遍历的顺序是「从左往右」
- 返回值:
根据「状态表⽰以及题⽬要求」,需要返回 dp[n] 位置的值。
class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {int n=cost.size();vector<int> dp(n+1);//初始化dp[0]=dp[1]=0;for(int i=2;i<=n;i++){dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);}return dp[n];}
};
解法2
- 状态表⽰:
dp[i] 表⽰:从 i 位置出发,到达楼顶,此时的最⼩花费。
- 状态转移⽅程:
根据最近的⼀步,分情况讨论:
▪ ⽀付 cost[i] ,往后⾛⼀步,接下来从 i + 1 的位置出发到终点: dp[i + 1] + cost[i]
▪ ⽀付 cost[i] ,往后⾛两步,接下来从 i + 2 的位置出发到终点: dp[i + 2] + cost[i]
我们要的是最⼩花费,因此 dp[i] = min(dp[i + 1], dp[i + 2]) + cost[i] 。
- 初始化:
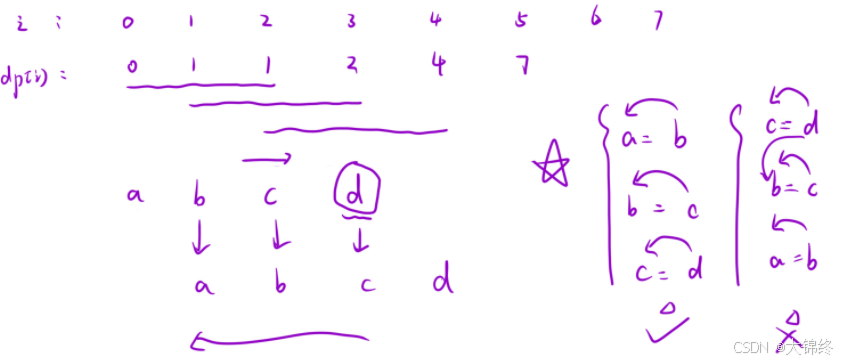
为了保证填表的时候不越界,我们需要初始化最后两个位置的值,结合状态表⽰易得: dp[n - 1] = cost[n - 1], dp[n - 2] = cost[n - 2]
- 填表顺序:
根据「状态转移⽅程」可得,遍历的顺序是「从右往左」。
- 返回值:
根据「状态表⽰以及题⽬要求」,需要返回 dp[n] 位置的值。注意,此时不需要多开辟一个空间,因为根据状态表示从n位置到n位置原地踏步的最小花费为0
class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {int n=cost.size();vector<int> dp(n);//初始化dp[n-1]=cost[n-1];dp[n-2]=cost[n-2];for(int i=n-3;i>=0;i--)//从右往左初始化{dp[i]=min(dp[i+1]+cost[i],dp[i+2]+cost[i]);}return min(dp[0],dp[1]);}
};
注意状态表示可以是多个的,如果能推得状态转移方程并且最后运行通过,证明该种状态表示是正确的
四. (91.) 解码⽅法(力扣)
4.1算法原理
- 状态表⽰:
根据以往的经验,对于⼤多数线性 dp ,经验上都是「以某个位置结束或者开始」做⽂章,这⾥继续尝试「⽤ i 位置为结尾」结合「题⽬要求」来定义状态表⽰。dp[i] 表⽰:字符串中 [0,i] 区间上,⼀共有多少种编码⽅法。
2.状态转移方程:
关于 i 位置的编码状况,我们可以分为下⾯两种情况:
i. 让 i 位置上的数单独解码成⼀个字⺟;
ii. 让 i 位置上的数与 i - 1 位置上的数结合,解码成⼀个字⺟
由状态定义不用考虑i+1位置的编码,i和i-1位置的解码都有成功和失败两种可能。
解码成功:
解码方法等于前一位区间上的解码方法,相当于前一位区间上所由解码结果后面再加上当前位置解码后的字母即可
解码失败:
说明当前位置上不能单独解码或结合解码,之前的努力都白费了
3.初始化
由于可能要⽤到 i - 1 以及 i - 2 位置上的 dp 值,因此要先初始化「前两个位置」。
初始化 dp[0] :结果有0,1
i. 当 s[0] == ‘0’ 时,没有编码⽅法,结果 dp[0] = 0 ;
ii. 当 s[0] != ‘0’ 时,能编码成功, dp[0] = 1
初始化 dp[1] :结果有0,1,2
i. 当 s[1] 在 [1,9] 之间时,能单独编码,此时 dp[1] += dp[0] (原因同上,
dp[1] 默认为 0 )
ii. 当 s[0] 与 s[1] 结合后的数在 [10, 26] 之间时,说明在前两个字符中,⼜有⼀种
编码⽅式,此时 dp[1] += 1
- 填表顺序:
「从左往右」
- 返回值:
应该返回 dp[n - 1] 的值,表⽰在 [0, n - 1] 区间上的编码⽅法。
class Solution {
public:int numDecodings(string s) {int n=s.size();vector<int> dp(n);//初始化if(s[0]!='0') dp[0]=1;//处理边界情况if(n==1) return dp[0];if(s[0]!='0'&&s[1]!='0') dp[1]=1;//注意条件判断时不能连续比较int t=(s[0]-'0')*10+(s[1]-'0');if(10<=t&&t<=26) dp[1]+=1;//填表for(int i=2;i<n;i++){//解码当前位置,单独if(s[i]!='0') dp[i]+=dp[i-1];//与上一位置共同解码int t=(s[i-1]-'0')*10+(s[i]-'0');if(10<=t&&t<=26) dp[i]+=dp[i-2];}return dp[n-1];}
};
可以看出上述代码初始化部分和循环部分代码有些重复,特别是初始化dp[1]位置时有三种情况需要判断,可以优化
4.2细节优化
dp表中多开辟一位,将dp[0]设置为辅助节点来初始化,这样原dp表中dp[1]位置初始化的复杂条件判断就可以避免,放到循环中去完成赋值,简化了一次操作
注意:
1.辅助节点中的值要保证后面的填表是正确的
已知会先初始化两个节点,一个为辅助节点(新dp表中dp[0]),另一个为旧dp表中的dp[0]新dp表中的dp[1]。填表前会先判断解码,单独解码时与前一个节点有关与辅助节点无关,但与前一节点共同解码时成功后会加上前前节点的解码方法数,所以此时与辅助节点有关,该情况下辅助节点应设为1而不是0
2.下标的映射关系
由于dp表中多增一位,在查找原表进行解码时下标位置要-1才能相对应
class Solution {
public:int numDecodings(string s) {int n=s.size();vector<int> dp(n+1);//初始化dp[0]=1;// 保证后续填表是正确的dp[1] = s[0] != '0';//填表for(int i=2;i<=n;i++){//解码当前位置,单独if(s[i-1]!='0') dp[i]+=dp[i-1];//与上一位置共同解码int t=(s[i-2]-'0')*10+(s[i-1]-'0');//改变下标映射关系if(10<=t&&t<=26) dp[i]+=dp[i-2];}return dp[n];}
};

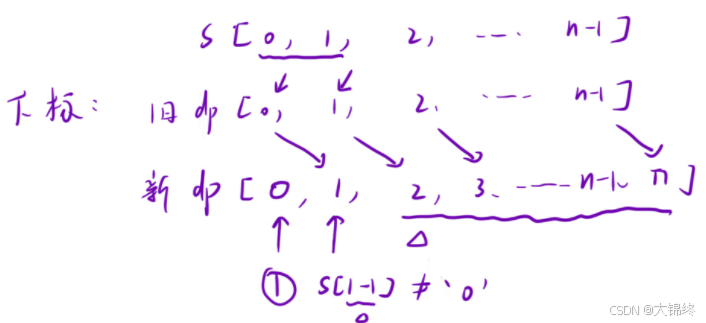



)



后端)



)
)





)
