😘个人主页：@Cx330❀

👀个人简介：一个正在努力奋斗逆天改命的二本觉悟生

📖个人专栏：《C语言》《LeetCode刷题集》《数据结构-初阶》

前言：上篇博客我们学习了有关树的概念和相关术语的介绍，那么这篇博客将带着大家实现二叉树的部分接口

---

目录

一、堆的概念与结构

二、堆的初始化

三、堆的销毁

四、堆的插入数据（包含向上调整算法的实现）

向上调整算法：

测试结果：

五、 堆的删除数据(含向下调整算法)

向下调整算法：

六、堆的取堆顶

七、堆排序的实现

版本一：

版本二（推荐）：

八、代码展现：

Heap.h：

Heap.c：

test.c：

---

一、堆的概念与结构

如果有一个关键码的集合K={}，把它所有的元素按照完全二叉树的顺序存储方式存储，这里堆的底层实现其实也就是一个数组。我们堆分为小堆和大堆。我们将根结点最大的堆叫做最大堆或大根堆，根结点最小的堆叫做最小堆或者小根堆。

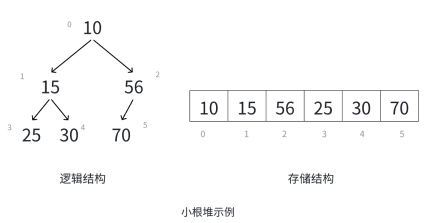
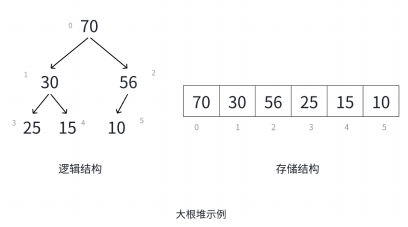
堆具有一下性质：

• 堆中某个结点的值总是不大于或者不小于其父结点的值
• 堆总是一颗完全二叉树
• 堆顶是最值(最大值或最小值)

🗒️二叉树性质：

对于具有n个结点的完全二叉树，如果按照从上至下从左至右的数组顺序对所有结点从0开始编号，则对于序号为i的结点有：

• 若i>0，i的位置结点的双亲序号：(i-1)/2；i=0，i为根结点编号，无双亲结点
• 若2i+1<n，左孩子序号：2i+1，2i+1>=n，则无左孩子
• 若2i+2<n，右孩子序号：2i+2，2i+2>=n，则无右孩子

堆的定义：

typedef int HPDataType;
typedef struct Heap
{HPDataType* arr;int size;int capacity;
}HP;

---

二、堆的初始化

//初始化
void HPInit(HP* php)
{assert(php);php->arr = NULL;php->capacity = php->size = 0;
}

这里没有过多强调的，都是很简单的

---

三、堆的销毁

//销毁
void HPDesTroy(HP* php)
{assert(php);if (php->arr)free(php->arr);php->arr = NULL;php->capacity = php->size = 0;
}

这里强调一下当堆不为空时进行free后再将数组置为NULL

---

四、堆的插入数据（包含向上调整算法的实现）

我们实现堆的插入大致思路都跟顺序表一样，但是在尾部插入一个数据后，原来的堆就改变了，我们需要把插入的数据调整到对应的位置上，我们先来看个图片吧(以大堆为例)

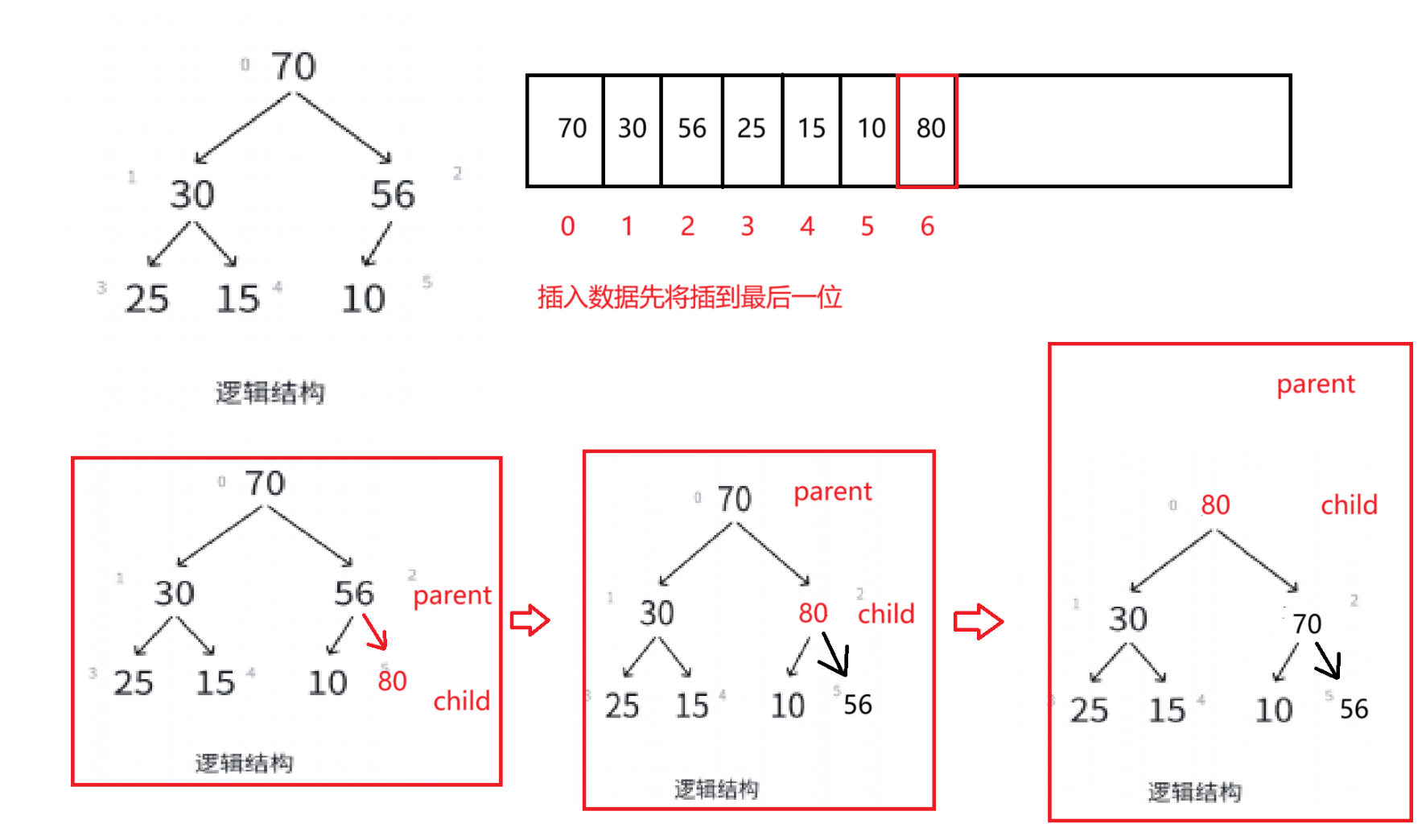
向上调整算法：

//交换
void Swap(int* x, int* y)
{int tmp = *x;*x = *y;*y = tmp;
}//向上调整
void AdjustUp(HPDataType* arr, int child)
{int parent = (child - 1) / 2; while (child > 0){//建大堆 >//建小堆 <if (arr[child] < arr[parent])//小堆{Swap(&arr[child],&arr[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}

这里如果child比parent要大，就进行交换，所以实现了小堆，循环到child>0就停止

堆的插入数据：

//插入数据
void HPPush(HP* php, HPDataType x)
{assert(php);//空间不够if (php->capacity == php->size){int newcapacity = php->capacity == 0 ? 4 : 2 * php->capacity;HPDataType* tmp = (HPDataType*)realloc(php->arr, newcapacity * sizeof(HPDataType));if (tmp == NULL){perror("realloc fail!");exit(1);}php->arr = tmp;php->capacity = newcapacity;}//空间足够php->arr[php->size] = x;//向上调整--变成有效堆结构AdjustUp(php->arr, php->size);++php->size;
}

首先判断堆的空间是否足够，如果不够要先进行增容，增容的代码已经写过许多遍了，这里就不过多强调了，空间足够了就直接在size位置插入，在向上调整，使之变为有效的堆结构，然后让size++即可

打印接口：

//打印
void HPPrint(HP* php)
{for (int i = 0; i < php->size; i++){printf("%d ", php->arr[i]);}printf("\n");
}

test.c：

void test01()
{HP hp;HPInit(&hp);HPPush(&hp, 25);HPPush(&hp, 15);HPPush(&hp, 10);HPPush(&hp, 80);HPPush(&hp, 56);HPPush(&hp, 30);HPPush(&hp, 70);HPDesTroy(&hp);
}int main()
{test01();return 0;
}

测试结果：

这里的测试结果没有错，打印出来个小堆

---

五、 堆的删除数据(含向下调整算法)

我们实现堆的删除需要的是头部操作，如果跟顺序表一样去移动数据的话会改变掉堆的结构，所以我们可以先交换首尾数据，然后再把尾上的数据删掉。然后再通过向下调整算法将堆再次调整成一个大堆

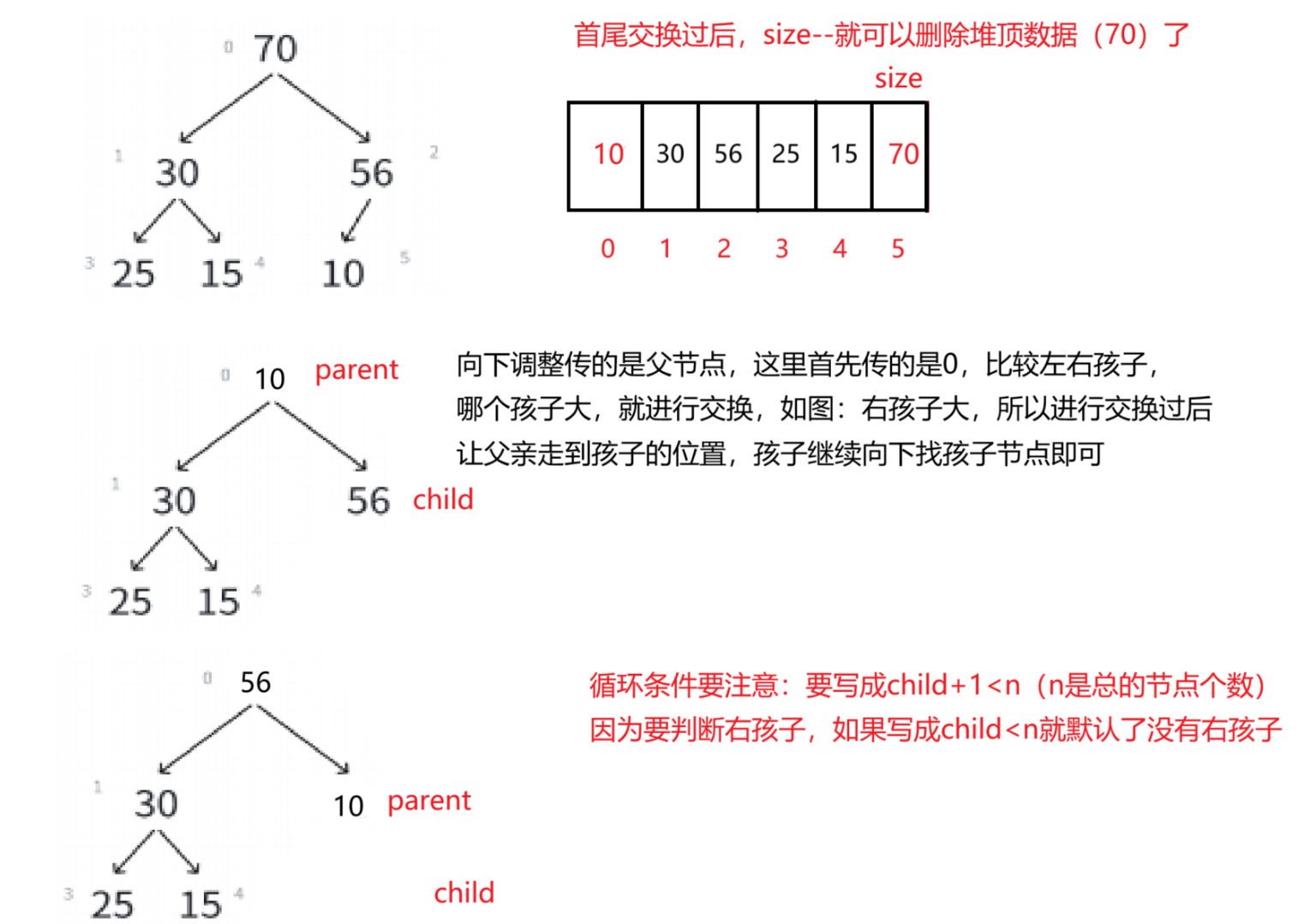
向下调整算法：

//向下调整
void AdjustDown(HPDataType* arr, int parent, int n)
{int child = parent * 2 + 1;while (child < n){//找大的孩子//建大堆 <//建小堆 >if (child + 1 < n && arr[child] > arr[child + 1])//小堆{child++;}//孩子和父亲比较//建大堆 <//建小堆 >if (arr[parent]> arr[child])//小堆{Swap(&arr[parent], &arr[child]);parent = child;child= parent * 2 + 1;}else{break;}}
}

如果child小于parent就进行交换，所以这里是小堆

有了这个之后，我们再实现一个判空的函数之后就可以来实现删除了，判空的代码如下：

//判断为空
bool HPEmpty(HP* php)
{assert(php);return php->size == 0;
}

删除数据(栈顶操作)：

//出堆（堆顶）
void HPPop(HP* php)
{assert(!HPEmpty(php));Swap(&php->arr[0], &php->arr[php->size-1]);--php->size;//堆顶数据向下调整AdjustDown(php->arr, 0, php->size);
}

判断不为空，将堆顶数据与最后一个数据进行交换，size--就删除了堆顶数据，然后进行向下调整

---

六、堆的取堆顶

//取堆顶
HPDataType HPTop(HP* php)
{assert(!HPEmpty(php));return php->arr[0];
}

堆不为空才可以取堆顶，堆顶数据就是数组首元素，直接取就可以

这里再补充一个求数据个数的接口：

//求size
int HPSize(HP* php)
{assert(php);return php->size;
}

在实现了取堆顶后，我们通过测试文件看一个很意思的操作

test.c:

void test01()
{HP hp;HPInit(&hp);HPPush(&hp, 25);HPPush(&hp, 15);HPPush(&hp, 10);HPPush(&hp, 80);HPPush(&hp, 56);HPPush(&hp, 30);HPPush(&hp, 70);HPPrint(&hp);while (!HPEmpty(&hp)){int top = HPTop(&hp);printf("%d ", top);HPPop(&hp);}HPDesTroy(&hp);
}int main()
{test1();
}

我们看打印出来的第二行发现，循环这个取顶部打印出堆的操作会将小堆有序(升序)的打印出来

那我们能不能试着实现堆排序呢？

---

七、堆排序的实现

我们堆排序的实现，其实有两种方式，但是呢第一种并不是真正的堆排序，因为它需要使用堆这个数据结构，但是第二种只是需要堆这个数据结构的思想。而且真正的堆排序建大堆是升序，小堆是降序。而第一种主要是模仿我们上面那个遍历取顶操作实现出来的，大堆反而是降序。但是我们还是把两种都一起看一下：

版本一：

//堆排序--这不是真正的堆排序
void HPSort(int* arr, int n)
{HP hp;HPInit(&hp);//把数组里的数据循环放到堆里for (int i = 0; i < n; i++){HPPush(&hp, arr[i]);}int i = 0;while (!HPEmpty(&hp)){int top = HPTop(&hp);arr[i++] = top;HPPop(&hp);}HPDesTroy(&hp);
}
int main()
{test01();int arr[6] = { 10,80,25,30,15,56 };printf("打印之前\n");for (int i = 0; i < 6; i++){printf("%d ", arr[i]);}printf("\n");HPSort(arr,6);//HeapSort(arr, 6);//BubbleSort(arr, 6);printf("打印之后\n");for (int i = 0; i < 6; i++){printf("%d ", arr[i]);}printf("\n");return 0;
}

测试结果：

这里就是先初始化一个堆，然后把数组里的元素插入到堆中，再利用循环遍历重复(取顶部数据放回数组后++到下一个后，删掉堆顶的操作）。由于是小堆所以每次取顶部取的都是当前堆中最小的数据，最后排出来的就是升序，这里还是特别注意一下，这严格来说不算真正的堆排序，它必须使用堆这个数据结构，而且真正的堆排序应该是大堆排升序，小堆排降序

版本二（推荐）：

//堆排序--使用的是队结构的思想n*logn
void HeapSort(int* arr, int n)
{//向下调整算法--建堆 时间复杂度O(n）for (int i = (n - 1 - 1)/2; i >=0; i--){AdjustDown(arr, i, n);//因为这里建的是小堆，所以向下调整，就成了降序}//向上调整算法--建堆  时间复杂度O(n*logn)/*for (int i = 0; i < n; i++){AdjustUp(arr, i);}*///n* lognint end = n - 1;while (end > 0)//循环取最后一个元素与顶交换，再向下调整{Swap(&arr[0], &arr[end]);AdjustDown(arr, 0, end);end--;}
}
int main()
{test01();int arr[6] = { 10,80,25,30,15,56 };printf("打印之前\n");for (int i = 0; i < 6; i++){printf("%d ", arr[i]);}printf("\n");HeapSort(arr, 6);//BubbleSort(arr, 6);printf("打印之后\n");for (int i = 0; i < 6; i++){printf("%d ", arr[i]);}printf("\n");return 0;
}

测试结果：

我们可以看出这个方法实现出来的就是非常标准的了，小堆排出来为降序。思路：取最后一颗子树的父节点，然后向下调整，调整最后一颗子树，后续先定义一个end=n-1的下标，然后遍历，重复交换首尾，向下调整(注意这里就是正常传了，父结点刚开始为0，然后是数组大小，我们传end就行，不会影响已经放到最后的)，end--的操作，最后end为0的时候结束，此时堆已经是一个从大到小的顺序了，因为我们每次的交换其实就是把当前顶部最大的放在最后，之后下次就不会再排它了。

这里我就不给大家画图了，但是大家一定要自己动手画图！！！

---

八、代码展现：

Heap.h：

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
typedef int HPDataType;
typedef struct Heap
{HPDataType* arr;int size;int capacity;
}HP;
//初始化
void HPInit(HP* php);
//销毁
void HPDesTroy(HP* php);
//交换
void Swap(int* x, int* y);
//插入数据
void HPPush(HP* php, HPDataType x);
//向上调整
void AdjustUp(HPDataType* arr, int child);
//向下调整
void AdjustDown(HPDataType* arr,int parent,int n);
//打印
void HPPrint(HP* php);
//判断为空
bool HPEmpty(HP* php);
//出堆（堆顶）
void HPPop(HP* php);
//取堆顶
HPDataType HPTop(HP* php);

Heap.c：

#include"Heap.h"
//初始化
void HPInit(HP* php)
{assert(php);php->arr = NULL;php->capacity = php->size = 0;
}//销毁
void HPDesTroy(HP* php)
{assert(php);if (php->arr)free(php->arr);php->arr = NULL;php->capacity = php->size = 0;
}//打印
void HPPrint(HP* php)
{for (int i = 0; i < php->size; i++){printf("%d ", php->arr[i]);}printf("\n");
}//交换
void Swap(int* x, int* y)
{int tmp = *x;*x = *y;*y = tmp;
}//向上调整
void AdjustUp(HPDataType* arr, int child)
{int parent = (child - 1) / 2; while (child > 0){//建大堆 >//建小堆 <if (arr[child] < arr[parent])//小堆{Swap(&arr[child],&arr[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}//向下调整
void AdjustDown(HPDataType* arr, int parent, int n)
{int child = parent * 2 + 1;while (child < n){//找大的孩子//建大堆 <//建小堆 >if (child + 1 < n && arr[child] > arr[child + 1])//xiao堆{child++;}//孩子和父亲比较//建大堆 <//建小堆 >if (arr[parent]> arr[child])//xiao堆{Swap(&arr[parent], &arr[child]);parent = child;child= parent * 2 + 1;}else{break;}}
}
//插入数据
void HPPush(HP* php, HPDataType x)
{assert(php);//空间不够if (php->capacity == php->size){int newcapacity = php->capacity == 0 ? 4 : 2 * php->capacity;HPDataType* tmp = (HPDataType*)realloc(php->arr, newcapacity * sizeof(HPDataType));if (tmp == NULL){perror("realloc fail!");exit(1);}php->arr = tmp;php->capacity = newcapacity;}//空间足够php->arr[php->size] = x;//向上调整--变成有效堆结构AdjustUp(php->arr, php->size);++php->size;
}//判断为空
bool HPEmpty(HP* php)
{assert(php);return php->size == 0;
}//出堆（堆顶）
void HPPop(HP* php)
{assert(!HPEmpty(php));Swap(&php->arr[0], &php->arr[php->size-1]);--php->size;//堆顶数据向下调整AdjustDown(php->arr, 0, php->size);
}//取堆顶
HPDataType HPTop(HP* php)
{assert(!HPEmpty(php));return php->arr[0];
}

test.c：

#include"Heap.h"
void test01()
{HP hp;HPInit(&hp);HPPush(&hp, 25);HPPush(&hp, 15);HPPush(&hp, 10);HPPush(&hp, 80);HPPush(&hp, 56);HPPush(&hp, 30);HPPush(&hp, 70);//HPPrint(&hp);/*HPPop(&hp);HPPrint(&hp);HPPop(&hp);HPPrint(&hp);HPPop(&hp);HPPrint(&hp);HPPop(&hp);HPPrint(&hp);*///while (!HPEmpty(&hp))//{//	int top = HPTop(&hp);//	printf("%d ", top);//	HPPop(&hp);//}HPDesTroy(&hp);
}
//堆排序--这不是真正的堆排序
void HPSort(int* arr, int n)
{HP hp;HPInit(&hp);//把数组里的数据循环放到堆里for (int i = 0; i < n; i++){HPPush(&hp, arr[i]);}int i = 0;while (!HPEmpty(&hp)){int top = HPTop(&hp);arr[i++] = top;HPPop(&hp);}HPDesTroy(&hp);
}//堆排序--使用的是队结构的思想n*logn
void HeapSort(int* arr, int n)
{//向下调整算法--建堆 时间复杂度O(n）for (int i = (n - 1 - 1)/2; i >=0; i--){AdjustDown(arr, i, n);//因为这里建的是小堆，所以向下调整，就成了降序}//向上调整算法--建堆  时间复杂度O(n*logn)/*for (int i = 0; i < n; i++){AdjustUp(arr, i);}*///n* lognint end = n - 1;while (end > 0)//循环取最后一个元素与顶交换，再向下调整{Swap(&arr[0], &arr[end]);AdjustDown(arr, 0, end);end--;}
}
//冒泡排序
void BubbleSort(int *arr,int n)
{for (int i = 0; i < n; i++){for (int j = 0; j < n - i - 1; j++){if (arr[j] < arr[j + 1]);{Swap(&arr[j], &arr[j + 1]);}}}
}
int main()
{//test01();int arr[6] = { 10,80,25,30,15,56 };printf("打印之前\n");for (int i = 0; i < 6; i++){printf("%d ", arr[i]);}printf("\n");//HPSort(arr, 6);HeapSort(arr, 6);//BubbleSort(arr, 6);printf("打印之后\n");for (int i = 0; i < 6; i++){printf("%d ", arr[i]);}printf("\n");return 0;
}

---

往期回顾：

【数据结构初阶】--树与二叉树预备篇

【数据结构初阶】--栈与队列（栈）

【数据结构初阶】--栈与队列（队列）

总结：这篇博客到这里就结束了，组要给大家讲了一些重要的排序算法（向上/下调整算法），大家还要注意要勤画图，我们还会证明向下调整和向上调整算法建堆的复杂度证明以及用链式结构来实现二叉树，大家可以很好的感觉到递归的暴力美学。如果文章对你有帮助的话，欢迎评论，点赞，收藏加关注，感谢大家的支持。