一.容器适配器

容器适配器的核心就像交流电适配器：

• 核心作用：对底层容器（如vector、deque）进行“包装”
• 关键效果：让原本的容器以特定数据结构（栈、队列等）形式呈现
• 核心价值：屏蔽底层复杂操作，只提供适配后结构的专属接口，精准满足特定场景的数据操作需求（如栈的“后进先出”、队列的“先进先出”）。

1. 本质：

封装底层容器，不直接存储数据

• 容器适配器本身不实现数据存储逻辑，而是通过封装现有基础容器（如 vector、deque、list 等）来实现功能。
• 底层容器的选择可手动指定（需满足适配器的接口要求），若不指定则使用标准库默认的底层容器（如 stack 默认用 deque）。

2. 接口：

受限且专注于适配后的数据结构逻辑

• 容器适配器仅提供适配后的数据结构的核心操作，屏蔽底层容器的复杂接口。
  例如：stack 仅提供 push()（栈顶插入）、pop()（栈顶删除）、top()（访问栈顶）等符合「后进先出（LIFO）」逻辑的操作；queue 仅提供 push()（队尾插入）、pop()（队头删除）等符合「先进先出（FIFO）」逻辑的操作。

3. 迭代器：

不支持迭代器访问，隐藏底层细节

• 容器适配器不对外暴露迭代器，用户无法通过迭代器遍历适配器中的元素。
• 这一设计的目的是严格限制数据操作方式，确保适配后的数据结构逻辑（如栈只能从栈顶操作）不被破坏。

4. 功能：

适配为特定数据结构

• 容器适配器的核心作用是将底层容器「适配」为常用的数据结构，标准库提供三种典型适配器：
  • stack：适配为栈（LIFO 结构）；
  • queue：适配为队列（FIFO 结构）；
  • priority_queue：适配为优先队列（元素按优先级自动排序）。

二.deque的简单介绍

1.概念与特性

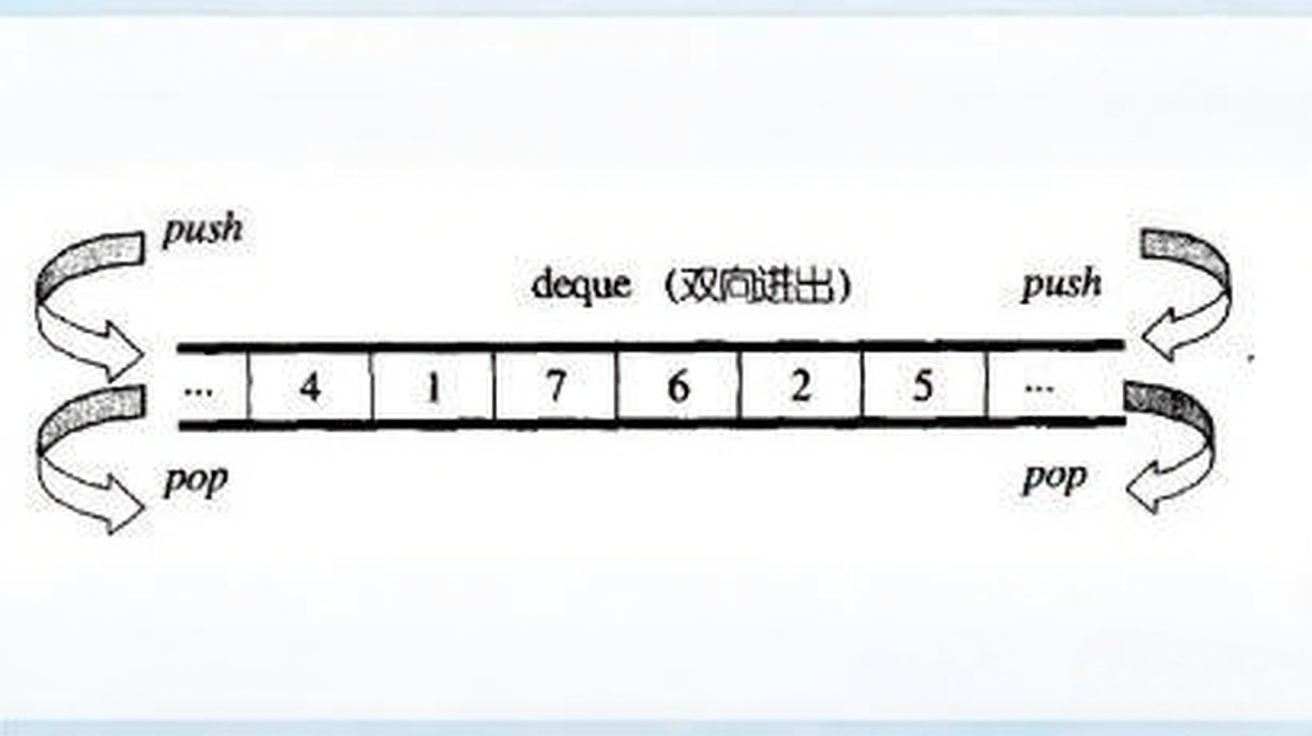
上图中展示的是双端队列（deque，Double-Ended Queue）的结构和操作方式。
双端队列是一种允许在队列两端进行插入和删除操作的线性数据结构，它结合了栈和队列的特性，支持在队列的前端（front）和后端（back）进行元素的添加（push）和移除（pop）操作。

在 C++ 标准库中，std::deque 是双端队列的实现，它具有以下特点：

优点：

1. 动态扩展：双端队列的大小可以动态变化，支持在运行时根据需要扩展或收缩。
2. 随机访问：虽然双端队列主要用于两端操作，但它也支持通过索引进行随机访问，这一点与 std::vector 类似。
3. 高效操作：在双端队列的两端进行插入和删除操作的时间复杂度是 O(1)，而在中间进行操作的时间复杂度是 O(n)。

缺点：

1. 中间操作低效：在非两端位置进行插入/删除，需移动大量元素，时间复杂度为 O(n)。
2. 内存碎片风险：由多段不连续内存块组成，频繁操作易产生内存碎片。
3. 内存开销较高：需额外存储内存块管理信息，内存占用多于 vector。
4. 迭代器稳定性差：扩容或结构变动时，迭代器、指针、引用可能全部失效。

2.结构与底层逻辑

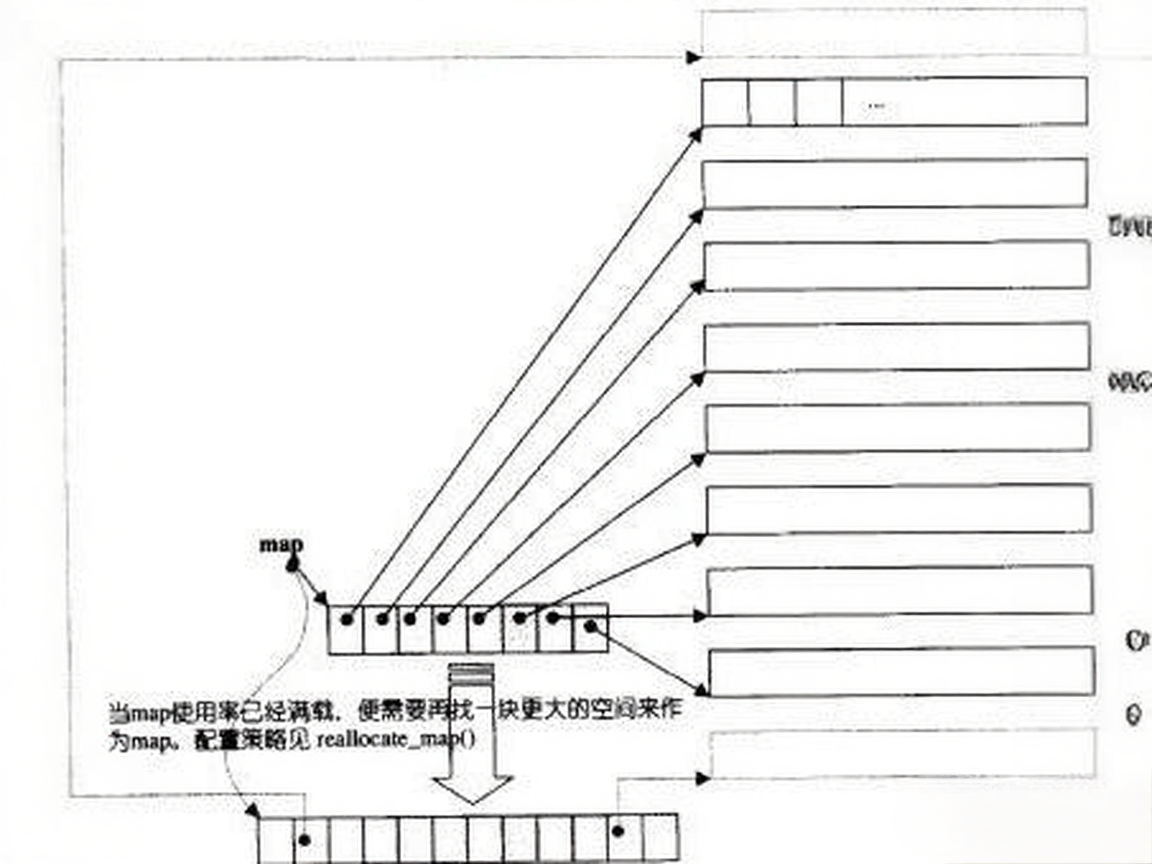
2.1 双端队列（deque）结构：

1. 分段存储：由多段连续内存块组成，通过 map（指针数组）管理这些块，实现逻辑上的连续。
2. 双向扩展：可从两端快速插入/删除（时间复杂度 O(1)），无需像 vector 那样整体扩容。
3. map 管理：map 存储内存块指针，当 map 满时需重新分配更大的 map 并复制指针（类似扩容）。
4. 随机访问：通过 map 定位内存块，再通过偏移量访问元素，时间复杂度 O(1)，但缓存局部性弱于 vector。
5. 中间操作劣势：在非两端位置插入/删除时，需移动元素，时间复杂度 O(n)，效率低于链表。

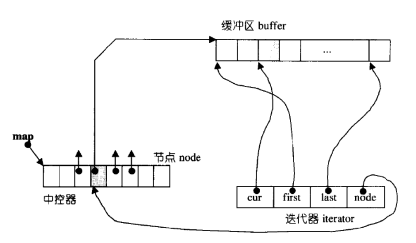
2.2 deque的内部结构

以上图片展示的是C++标准库中双端队列（deque）的内部结构。以下是图中各部分的核心要点：

1. 缓冲区（buffer）：存储实际数据的连续内存块，多个缓冲区通过map管理。
2. map：指针数组，每个指针指向一个缓冲区，实现逻辑上的连续。
3. 迭代器（iterator）：包含四个关键成员：
   • cur：指向当前元素的指针。
   • first：指向当前缓冲区起始位置的指针。
   • last：指向当前缓冲区末尾位置的指针。
   • node：指向map中当前缓冲区指针的指针。
4. 中控器：管理map的分配与扩容，确保deque动态扩展的稳定性。
5. 节点（node）：map中的元素，每个节点对应一个缓冲区的指针。

这种结构使得deque能够高效地在两端进行插入和删除操作，同时支持随机访问。

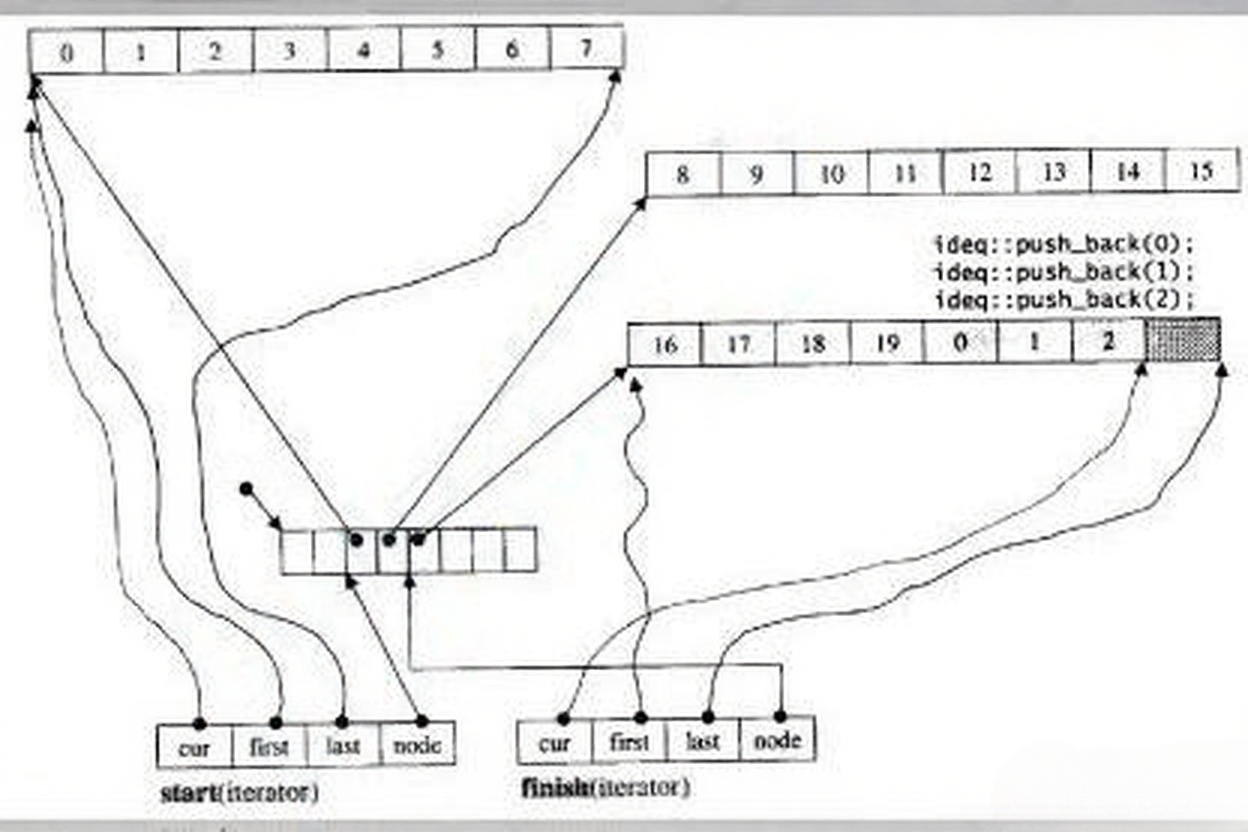
2.3 deque的插入与删除操作：

1. 插入操作：
   • 两端插入：通过push_back和push_front实现，时间复杂度为O(1)。在对应端的缓冲区末尾或起始位置直接添加元素，若缓冲区已满则自动分配新缓冲区。
   • 中间插入：通过insert实现，时间复杂度为O(n)。需要移动插入位置之后的所有元素，效率较低。
2. 删除操作：
   • 两端删除：通过pop_back和pop_front实现，时间复杂度为O(1)。直接移除对应端的元素，若缓冲区为空则释放该缓冲区。
   • 中间删除：通过erase实现，时间复杂度为O(n)。需要移动删除位置之后的所有元素，效率较低。
3. 内存管理：
   • 插入时若缓冲区满，会自动分配新缓冲区，并更新map中的指针。
   • 删除时若缓冲区为空，会自动释放该缓冲区，并更新map中的指针。

3.总结

3.1 deque和list,vector对比

deque 像是 vector 和 list 的结合：

• 兼具 vector 的随机访问能力（通过分段连续内存实现）和 list 的两端高效操作特性（O(1) 时间复杂度）。
• 避免了 vector 头部操作低效和扩容成本高的问题，也缓解了 list 随机访问差、缓存友好性低的缺陷。
• 但中间操作效率不及 list，随机访问性能略逊于 vector，是一种平衡型选择。

3.2 常用vector或list,而不是deque

多数情况选 vector 或 list 而非 deque，因：

1. 场景适配更精准：vector 强于随机访问，list 强于中间操作，覆盖多数需求；
2. 性能更稳定：deque 随机访问略逊于 vector，中间操作远不如 list；
3. 更简单直观：vector/list 实现和特性更易理解，使用更稳妥。

三.仿函数初步

在C++中，仿函数（Functor） 是一种特殊的对象，它可以像函数一样被调用。从技术上讲，仿函数是实现了operator()重载的类或结构体的实例，这使得对象可以使用函数调用语法（如obj()）来执行操作。

1.仿函数的特点

1. 行为类似函数，但可以保存状态（成员变量）
2. 可以像函数一样作为参数传递
3. 比普通函数更灵活，因为可以携带额外数据
4. 常用于STL算法中（如排序、查找等）

2.仿函数的基本实现

实现“小于比较”的仿函数功能

#include<iostream>
using namespace std;
namespace yl {// 定义模板类 less，用于实现“小于比较”的仿函数功能template<class T>class less{public:bool operator()(const T& x, const T& y){return x < y;}};
}int main(){yl::less<int> lessfunc;
cout << lessfunc(1, 2)<<endl;return 0;
}

仿函数优化冒泡排序

#include <iostream>
#include <vector>
using namespace std;// 仿函数：升序比较
template <typename T>
struct Less {bool operator()(const T& a, const T& b) const {return a < b; }
};// 仿函数：降序比较
template <typename T>
struct Greater {bool operator()(const T& a, const T& b) const {return a > b; }
};// 通用冒泡排序函数，通过仿函数定制比较规则
template <typename T, typename Compare>
void bubbleSort(vector<T>& arr, Compare comp) {int n = arr.size();for (int i = 0; i < n - 1; ++i) {for (int j = 0; j < n - i - 1; ++j) {// 调用仿函数的()运算符进行比较if (comp(arr[j], arr[j + 1])) { swap(arr[j], arr[j + 1]);}}}
}int main() {vector<int> arr = {64, 34, 25, 12, 22, 11, 90};// 用Less仿函数，升序排序bubbleSort(arr, Less<int>());cout << "升序排序结果：";for (int num : arr) {cout << num << " ";}cout << endl;// 重置数组arr = {64, 34, 25, 12, 22, 11, 90};// 用Greater仿函数，降序排序bubbleSort(arr, Greater<int>());cout << "降序排序结果：";for (int num : arr) {cout << num << " ";}cout << endl;return 0;
}

3.仿函数，普通函数，函数指针

对比维度	普通函数	函数指针	仿函数
本质	一段可执行代码块	指向函数的指针变量（内存地址）	重载了()运算符的类/结构体实例
状态管理	无状态，依赖参数/全局变量	无状态，依赖所指函数的状态管理	通过成员变量保存状态，每个实例独立
调用方式	直接通过函数名调用	通过指针变量间接调用	像函数一样调用对象（obj()）
行为灵活性	逻辑固定，修改需重写函数	可指向不同函数改变行为	可通过构造函数配置行为，同类型可有不同实例
作为参数传递	可直接传递函数名	传递指针变量	传递对象实例
类型信息	仅函数签名	仅表示函数签名	自身是类类型，携带完整类型信息
泛型编程适配性	适配性一般	模板中适配性差，难优化	易被模板推导，编译器可内联优化
扩展性	扩展需新增函数	扩展依赖新增函数并重新指向	可通过继承等面向对象特性扩展

总结：

1. 普通函数

   • 核心价值：最基础的可调用单元，语法简单直接
   • 关键局限：行为完全固定，无法动态调整或携带状态

2. 函数指针

   • 核心价值：通过指向不同函数，实现行为动态切换（解耦调用者与具体实现）
   • 关键局限：仍无状态管理能力，本质是"函数地址的容器"

3. 仿函数

   • 核心突破：同时具备函数调用能力与对象状态管理（通过成员变量保存上下文）
   • 关键优势：在泛型编程中表现最优——既能像函数一样被调用，又能通过对象属性定制行为，且易被编译器优化

简言之：普通函数是"固定行为"，函数指针是"可变行为但无记忆"，仿函数是"可变行为且有记忆"。

四.优先队列（priority_queue）的简单介绍

1.核心本质

• 是容器适配器，基于“严格弱排序”规则维护元素，默认保证队首（堆顶）始终是当前队列里“最大元素”（大根堆特性 ，也可通过仿函数改小根堆），逻辑类似堆结构

2.核心操作特点

• 支持插入元素（随时往队列里加元素），但只能访问/删除堆顶（最大/指定规则的优先级最高元素） ，类似堆的 top 访问、push 插入、pop 弹出逻辑

3.底层实现依赖

• 基于容器适配器封装底层容器（如 vector/deque，默认用 vector ），需底层容器支持：
  • 基础操作：empty()（判空）、size()（元素个数）、push_back()（尾插）、pop_back()（尾删 ，但优先队列逻辑上是从“堆顶”删，实际通过交换+尾删实现）
  • 迭代器要求：需随机访问迭代器（像 vector/deque ，list 是双向迭代器，不满足默认 priority_queue 需求，你自定义 queue 用 list 是因为自己封装逻辑没严格限制迭代器 ）

4.关键接口（以你的代码+标准库逻辑为例）

接口	功能说明
priority_queue()	构造空优先队列
priority_queue(first, last)	用迭代器区间 [first, last) 初始化，内部自动建堆
empty()	判断是否为空
top()	返回堆顶元素（最大/自定义优先级最高）
push(x)	插入元素 x，插入后会调整堆结构维持优先级规则
pop()	删除堆顶元素（实际先交换堆顶和尾元素，删尾元素，再调整堆结构）

5.总结

简单说，标准库 priority_queue 就是“自动维护堆结构的适配器”，借助底层容器+堆调整函数，让用户方便用“堆”的特性（始终访问优先级最高元素），你代码里自己实现的 priority_queue 也复刻了这个思路，只是死循环问题导致运行异常，修复后就能正常体现优先队列（大根堆）逻辑

五.priority_queue的模拟实现

1.头文件"priority_queue.h"

#pragma once
#include<iostream>
#include<functional>
#include<vector>
#include<cassert>
using namespace std;namespace yl
{template<typename T,typename container=vector<T>>class priority_queue{private://子结点中有一个大于父结点就可以向下调整void adjust_down(size_t parent) {size_t child = parent * 2 + 1;  // 左孩子初始位置while (child < _con.size()) {// 先找到左右孩子中值较大的那个if (child + 1 < _con.size() && _con[child + 1] > _con[child]) {child++;  // 右孩子更大，指向右孩子}// 如果最大的孩子大于父节点，交换并继续向下调整if (_con[child] > _con[parent]) {swap(_con[child], _con[parent]);parent = child;child = parent * 2 + 1;}else {// 父节点大于等于子节点，堆性质已满足，退出循环break;}}}// 向上调整函数：用于维护大根堆性质（当插入新元素时）// 从指定子节点开始，向上与父节点比较并交换，直到满足堆条件void adjust_up(size_t child){// 计算父节点索引（堆的父节点计算公式）size_t parent = (child - 1) / 2;// 当子节点索引大于0时（未到达根节点），继续调整while (child > 0){// 若子节点值大于父节点值，违反大根堆性质，需要交换if (_con[child] > _con[parent]){swap(_con[child], _con[parent]);// 更新子节点为原父节点位置，继续向上调整child = parent;// 计算新的父节点索引parent = (parent - 1) / 2;}else{// 子节点值小于等于父节点，已满足大根堆性质，退出调整break;}}}public:priority_queue() = default;//强制生成默认构造template<typename InputIterator>priority_queue(InputIterator first,InputIterator last):_con(first,last){//向下调整算法建堆for (size_t i = (_con.size() - 2) / 2; i < _con.size() && i >= 0; i--){//i < _con.size() && i >= 0 作为循环条件://i < _con.size() 防止 i 越界（理论上 i 从(size - 2) / 2 递减到 0，不会越界，但加上更安全）。// i >= 0 利用 size_t 的无符号特性：// 当 i 减到 0 后，再执行 --i 会变成 SIZE_MAX（一个极大的无符号数），此时 i >= 0 会失效，循环终止。adjust_down(i);}}// 插入元素void push(const T& x){_con.push_back(x);// 对新插入的元素（位于末尾）进行向上调整，维护堆性质adjust_up(_con.size() - 1);}// 从堆中删除顶部元素（堆顶为最大值）void pop(){// 交换堆顶元素与最后一个元素（便于后续删除最后一个元素）swap(_con[0], _con[_con.size() - 1]);  _con.pop_back();// 对新的堆顶元素进行向下调整，维护堆性质adjust_down(0);}// 获取最大值（这里建的是大堆）const T& top()const{return _con[0];}// 获取元素的个数size_t size(){return _con.size();}bool empty() const{return _con.empty();}private:container _con;};
}

2.测试文件"test.cpp"

#include"priority_queue.h"void test01()
{vector<int> v = { 1,23,14,51,66,73,29,30 };yl::priority_queue<int,vector<int>> pq(v.begin(),v.end());while (!pq.empty()){cout << pq.top() << " ";pq.pop();}cout << endl;
}
int main()
{test01();return 0;
}

输出结果如下：