🔥个人主页:胡萝卜3.0
🎬作者简介:C++研发方向学习者
📖个人专栏: 《C语言》《数据结构》 《C++干货分享》
⭐️人生格言:不试试怎么知道自己行不行

正片开始之前,我们来了解一下我们即将要来介绍、学习的这个数据结构——二叉树。
二叉树的作用:
(1)快速查找
二叉树(尤其是二叉排序树)可以用于高效的数据查找,其查找的时间复杂度为 O(logn),最坏情况下为O(n)。这种特性使得二叉树特别适合需要频繁查找、插入和删除操作的场景。(2)动态数据管理
由于二叉树支持动态查询,并且可以通过调整树的结构来优化性能(例如 AVL 树、红黑树),它被广泛应用于需要动态管理数据的场景,如数据库索引和内存管理。(3)有序序列生成
中序遍历一棵二叉排序树可以得到一个关键字的有序序列,这使得二叉树成为一种有效的排序工具。构造二叉排序树的过程本质上就是对无序序列进行排序的过程。(4)树状结构表示
许多现实世界的问题可以用树状结构来建模,例如网站目录结构、文件系统等。虽然这些结构可能不是严格的二叉树,但通过适当的转换,它们可以使用二叉树的相关算法来处理。
应用场景:
(1)网页爬虫中的遍历
在互联网工程中,当需要下载某个网站的所有网页时,可以利用二叉树的遍历算法来模拟这一过程。这种算法能够确保所有页面都被访问到,并且按照一定的顺序进行处理。(2)二叉树的展开
在某些特定的应用中,比如将二叉树转换为链表形式,可以通过递归的方式实现。例如,在先序遍历的顺序下,左子树会被移到右指针位置,而左子树的最后一个节点会指向原来的右子树。(3)平衡二叉树的应用
平衡二叉树(如 AVL 树、红黑树)通过保持树的高度平衡来确保查找、插入和删除操作的时间复杂度始终为O(logn)。这类树结构广泛应用于需要高性能数据检索的场景,例如数据库索引和操作系统调度器。(4)表达式树
表达式树是一种特殊的二叉树,其中叶子节点表示操作数,内部节点表示运算符。这种结构可以用于解析和求值数学表达式,并且在编译器设计中具有重要应用。(5)哈夫曼编码
哈夫曼树是一种带权路径长度最短的二叉树,常用于数据压缩领域。通过构建哈夫曼树,可以生成最优前缀编码,从而减少存储空间或传输成本。(6)决策树
在机器学习和人工智能领域,二叉树可以用来表示决策过程。每个节点代表一个特征判断,每个分支代表一个可能的结果,最终的叶子节点则代表最终的决策结果。
二叉树这个部分学起来不会容易,但是会让你觉得很有收获,你慢慢会觉得学二叉树很爽!
目录
正文
一、树
1.1 树的概念与结构
1.2 非树形结构
1.3 树的相关术语
1.4 树的表示方法--孩子兄弟表示法
1.5 属性结构实际运用场景
二、二叉树
2.1 二叉树的概念与结构
2.2 特殊的二叉树
2.2.1 满二叉树
2.2.2 完全二叉树
三、二叉树的存储结构
3.1 顺序结构
3.2 链式结构
正文
一、树
树是什么?数据结构中的树和自然界中的树有什么联系吗?有。


树的根在地下,故曰“向阳而生”;树形结构的根在上面——
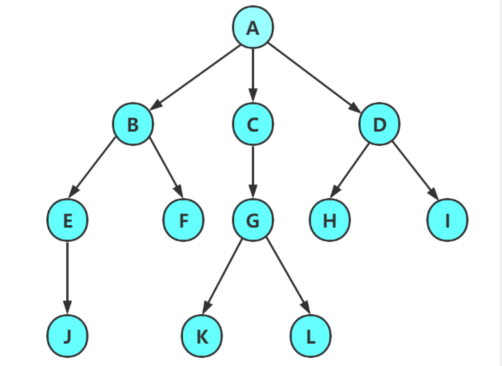
1.1 树的概念与结构
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次结构的集合。我们把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
- 有一个特殊的结点,称为根节点,根节点没有前驱结点。(根节点称为父节点/双亲结点)
- 除根节点外,其余结点被分成M(M>0)个互不相交的集合(T1、T2、……、Tm),其中每一个集合Ti(1<=i<=m)又是一棵结构与树类似的子树。每棵树的根节点有且只有一个前驱,可以有0个或者多个后继。因此,树是递归定义的。
1.2 非树形结构
在树形结构中,子树之间不能有交集,否则就不是树形结构!!!如果子树之间有交集,那就是非树形结构
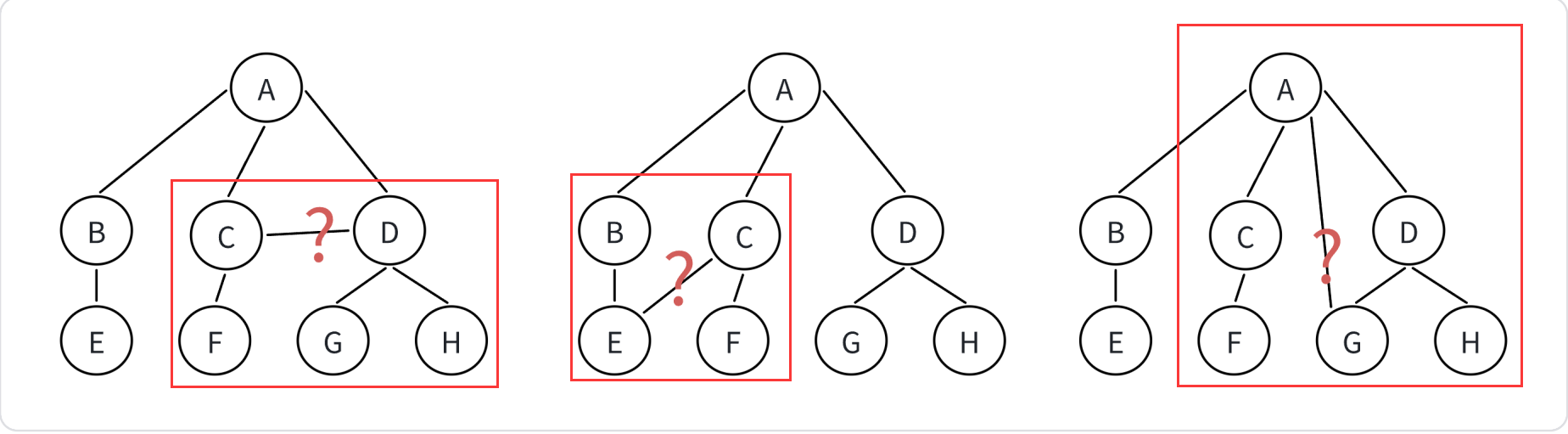
上图中的三个都是非树形结构,红方框内的子树有交集
注意:
- 子树是不相交的(如果存在相交就是图了,图以后得课程会有讲解)
- 除了根结点外,每个结点有且仅有一个父节点
- ⼀棵N个结点的树有N-1条边(记忆方式:2个结点有一条边)
1.3 树的相关术语
下图就是一个树形结构——
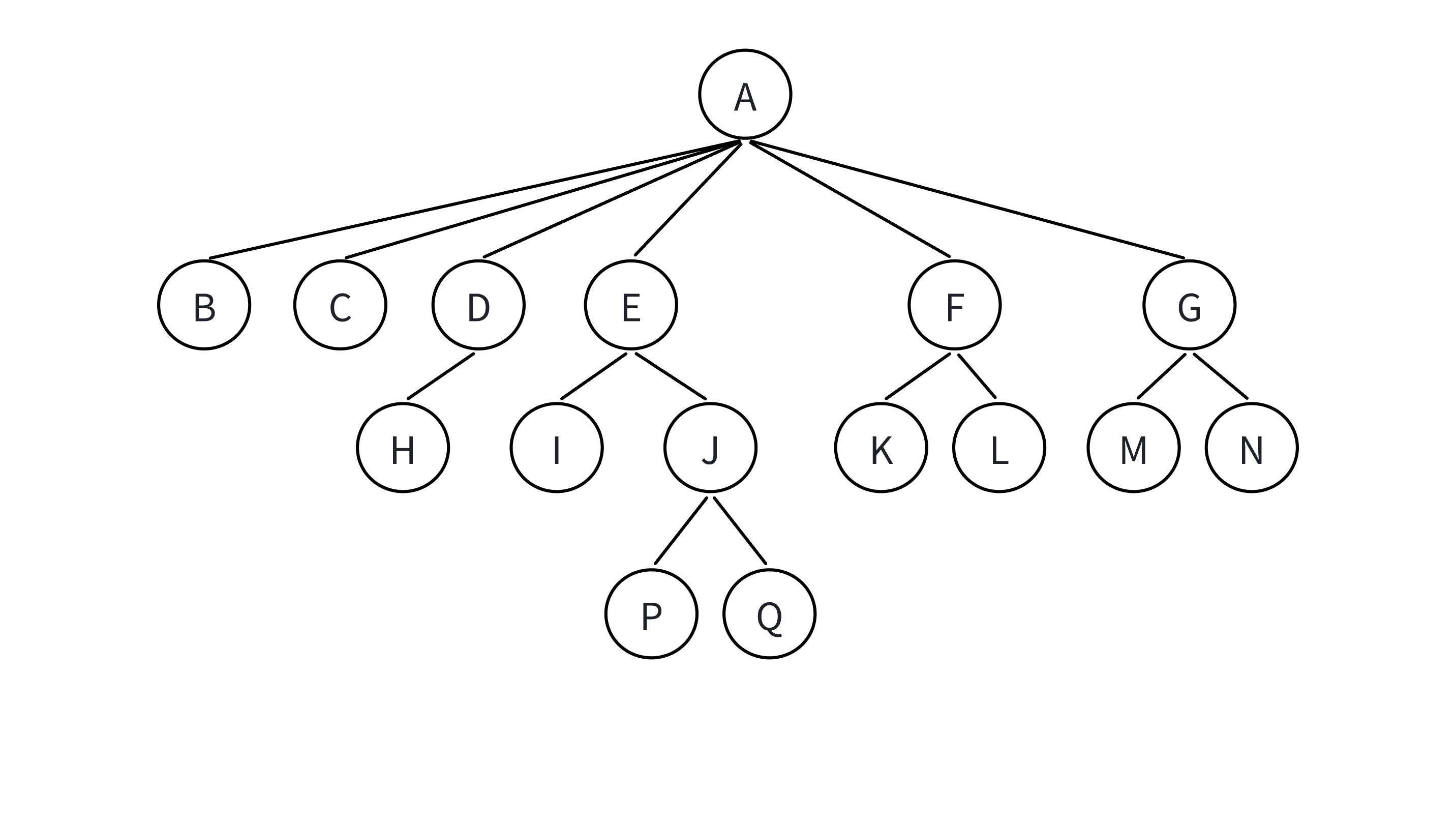
父结点/双亲结点:若一个结点含有子结点,则这个结点称为其子结点的父结点,如上图:A是B的父结点。
子结点/孩子结点:一个结点含有的子树的根结点称为该结点的子结点,如上图:B是A的孩子结点。
结点的度:一个结点有几个孩子,他的度就是多少,比如A的度为6,F的度为2,K的度为0。
树的度:一棵树中,最大的结点的度称为树的度,如上图:树的度为6。
叶子结点/终端结点:度为0的结点称为叶结点,如上图: B、C、H、I . . .等结点为叶结点。
分支结点/非终端结点:度不为0的结点,如上图: D、E、F、G... 等结点为分支结点。
兄弟结点:具有相同父结点的结点互称为兄弟结点(必须是亲兄弟),如上图: B、C 是兄弟结点。
结点的层次:从根开始定义起,根为第 1 层,根的子结点为第 2 层,以此类推。
树的高度或深度:树中结点的最大层次,如上图:树的高度为4。
结点的祖先:从根到该结点所经分支上的所有结点,如上图: A 是所有结点的祖先。
路径:一条从树中任意节点出发,沿父结点 - 子节点连接,达到任意节点的序列,比如A到Q的路径为: A-E-J-Q、H到Q的路径H-D-A-E-J-Q。
子孙:以某结点为根的子树中任一结点都称为该结点的子孙,如上图:所有结点都是A的子孙。
森林:由m(m>0)棵互不相交的树的集合称为森林。
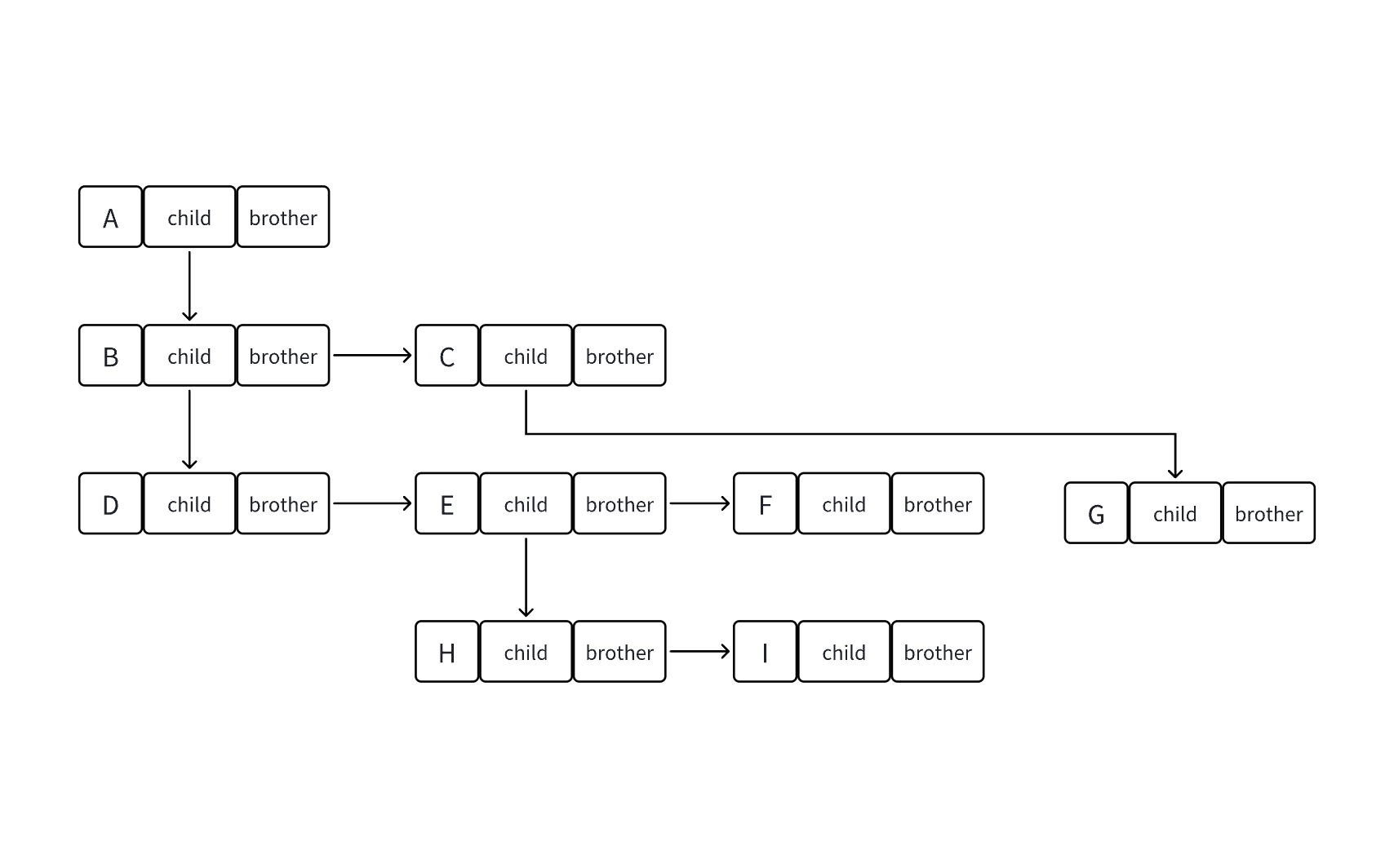
1.4 树的表示方法--孩子兄弟表示法
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,既要保存值域,也要保存结点和结点之间的关系,实际中树有很多种表示方式如:双亲表示法,孩子表示法、孩子双亲表示法以及孩子兄弟表示法等。我们这里就简单的了解其中最常用的孩子兄弟表示法:
struct TreeNode
{struct Node* child; // 左边开始的第⼀个孩⼦结点struct Node* brother; // 指向其右边的下⼀个兄弟结点int data; // 结点中的数据域
}比如说下面这幅图中的树结构:
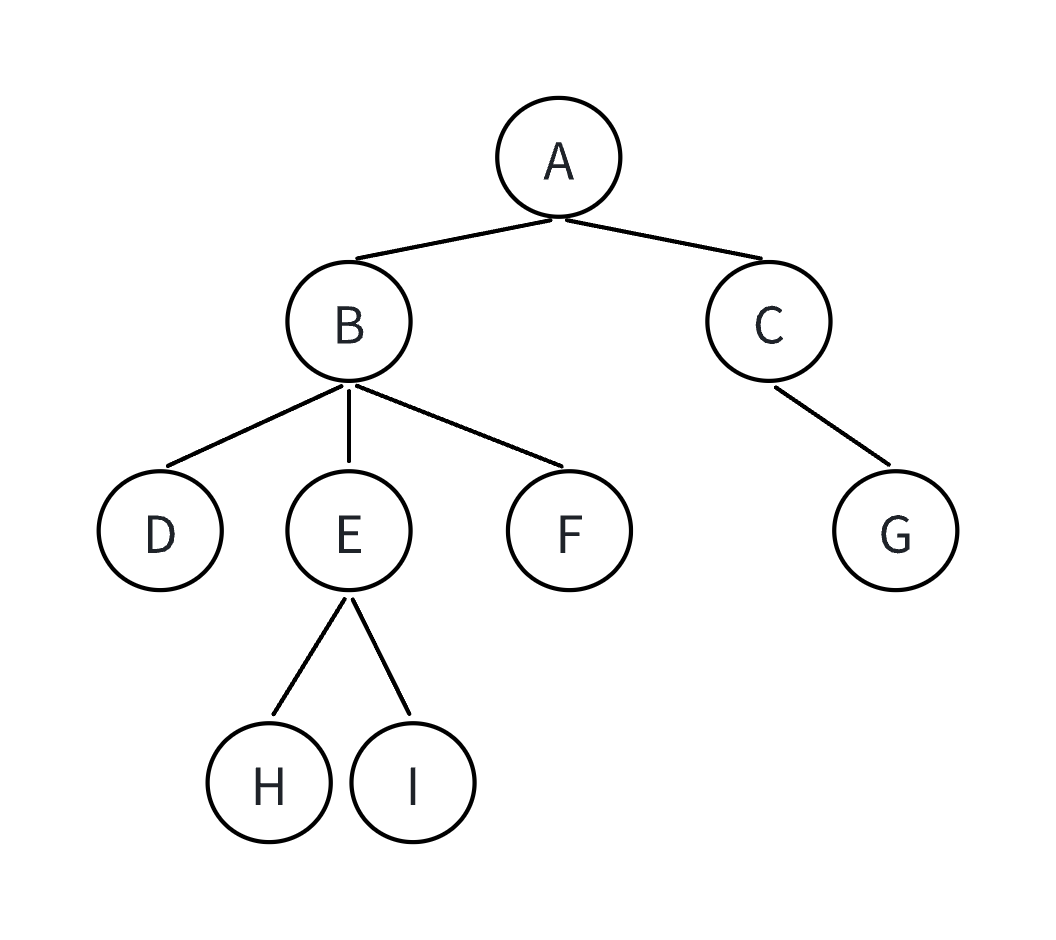
我们用孩子兄弟表示法可以这样表示——
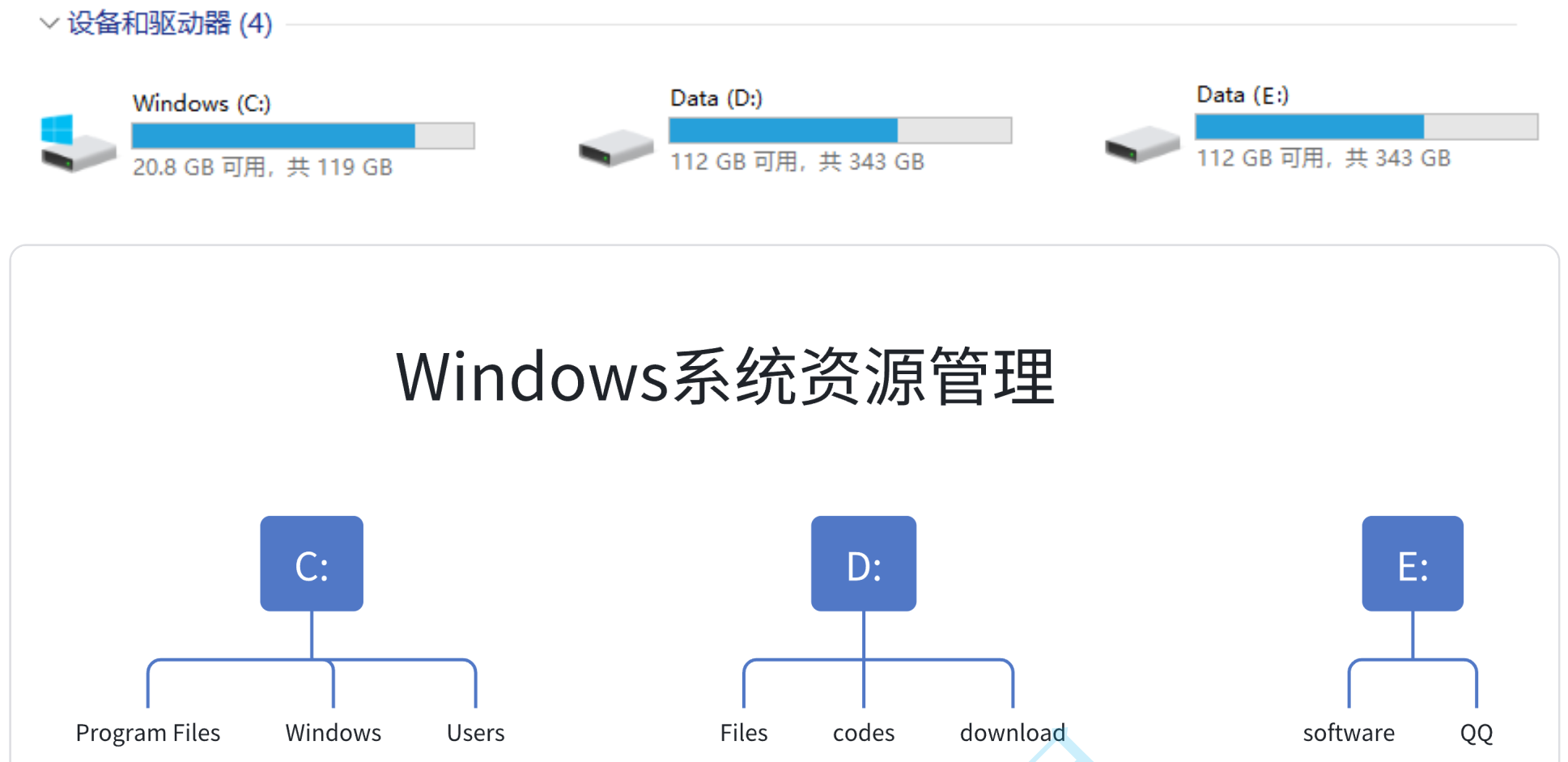
1.5 属性结构实际运用场景
文件系统是计算机存储和管理文件的一种方式,它利用树形结构来组织和管理文件和文件夹。在文件系统中,树结构被广泛应用,它通过父结点和子结点之间的关系来表示不停层级的文件和文件夹之间的关联。
二、二叉树
2.1 二叉树的概念与结构
在树形结构中,我们最常用的就是二叉树,一棵二叉树是结点的一个有限集合,该集合由一个根节点加上两棵分别称为左子树和右子树的二叉树组成或者二叉树为空。
结构:
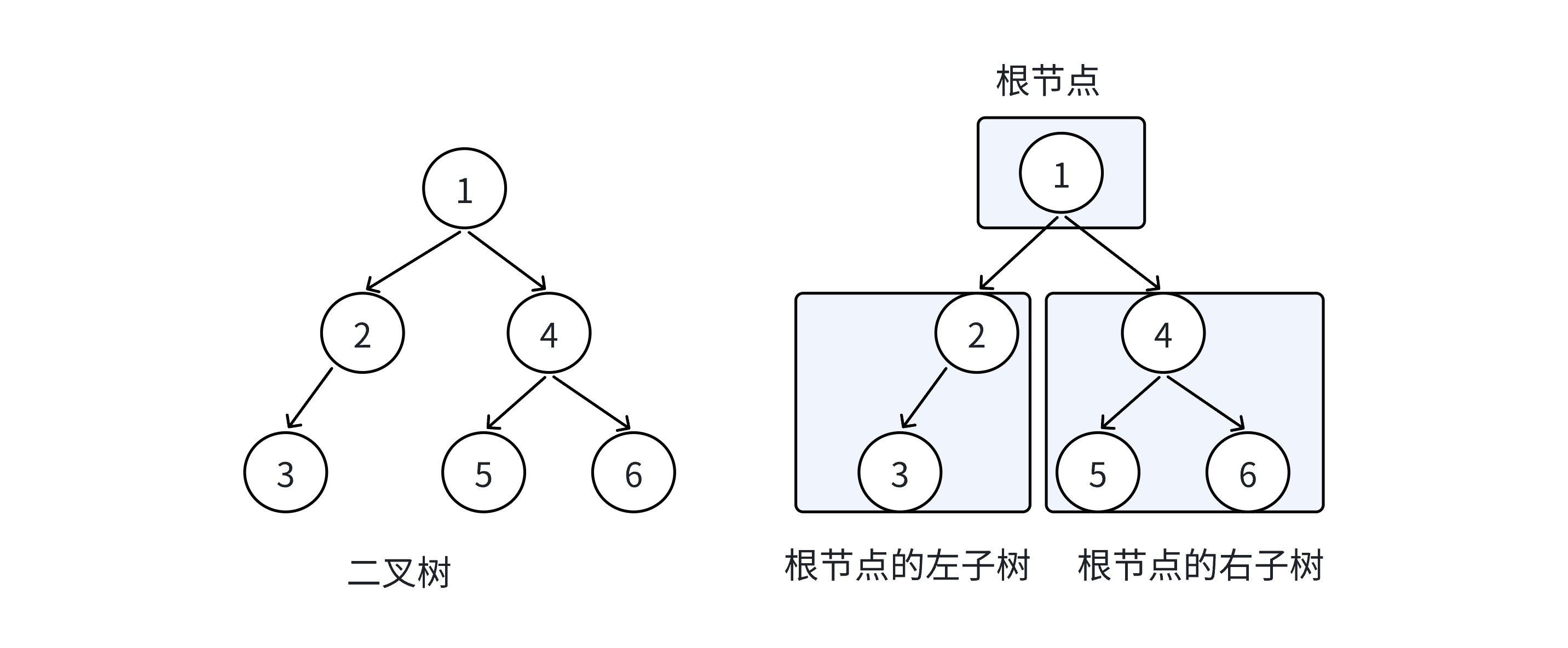
从上图可以看出:
- 二叉树不存在度大于2的结点(0,1,2)
- 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
注意:对于任意的⼆叉树都是由以下几种情况复合而成的:
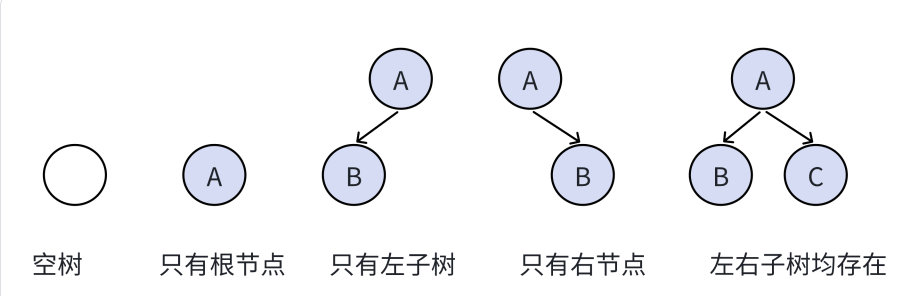
因此二叉树不是很好驾驭,于是我们定义了特殊的二叉树,比如满二叉树、完全二叉树等。
2.2 特殊的二叉树
树->二叉树->特殊的二叉树->满二叉树
2.2.1 满二叉树
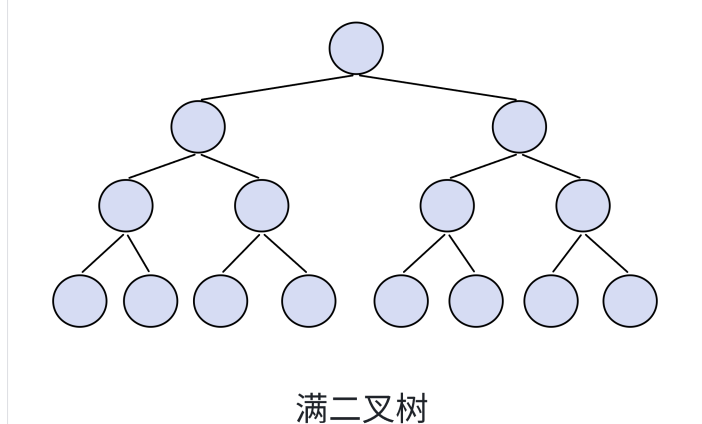
满二叉树(度为2,即最大结点个数为2),每一层结点数都最大,层数为K,结点总数为2^(k-1),这就是满二叉树。
满二叉树的结点总数是怎么求出来的呢?
2.2.2 完全二叉树
完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。
简单来说
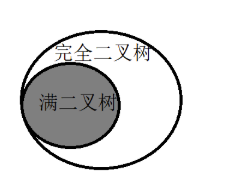
完全二叉树就是:除了最后一层,其他每层结点个数都达到最大,最后一层结点个数不一定达到最大,满二叉树就是完全二叉树的一种,并且完全二叉树的结点从左向右依次排列。
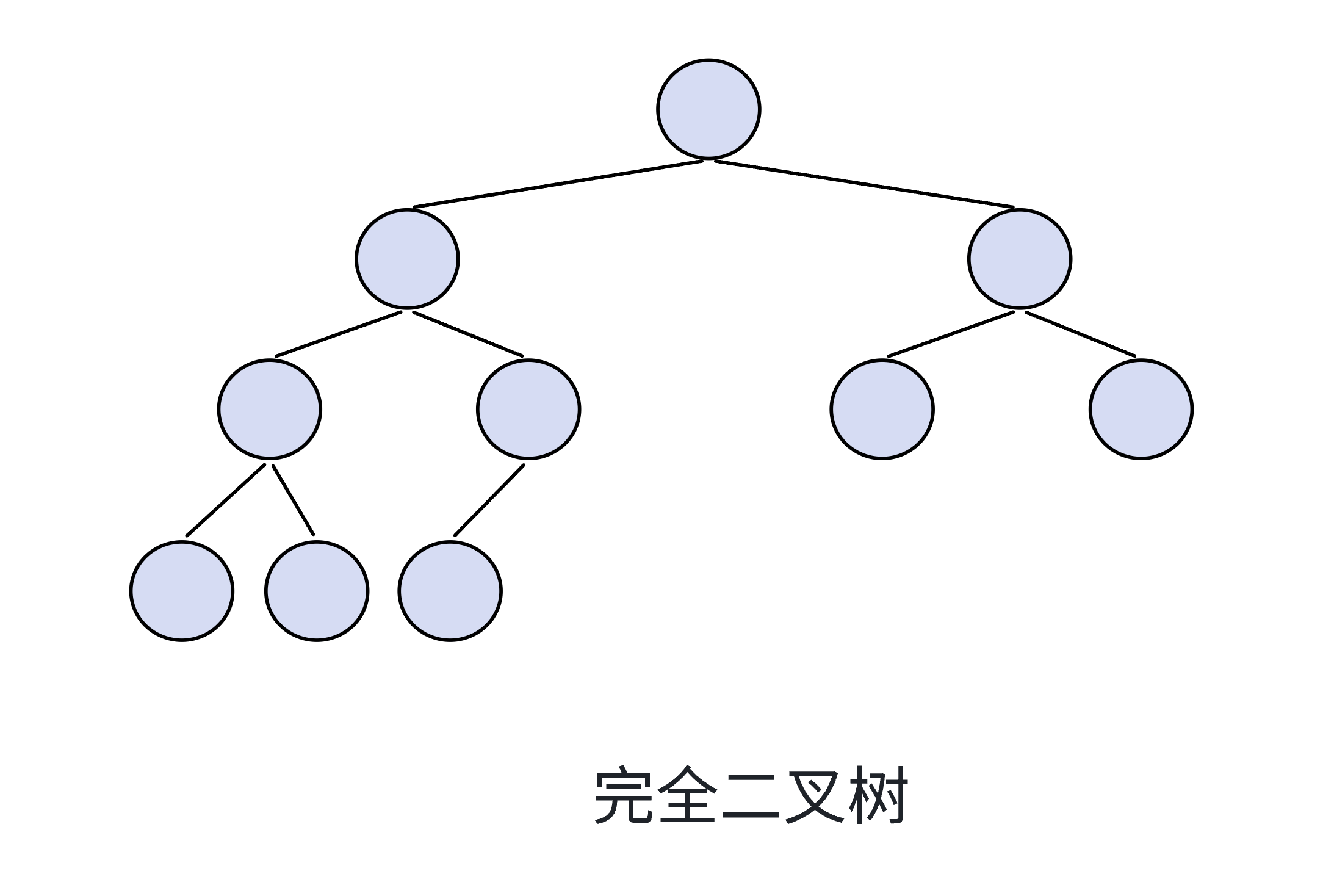
完全二叉树就是:除了最后一层,其他每层结点个数都达到最大,最后一层结点个数不一定达到最大,满二叉树就是完全二叉树的一种,并且完全二叉树的结点从左向右依次排列。
完全二叉树的每层结点的个数达到最大就是满二叉树;除了最后一层,其他每层结点个数都达到最大就是完全二叉树
完全二叉树的结点是从左往右依次排列的——
这是非常重要的一个知识点,观察下图,是不是一个完全二叉树——
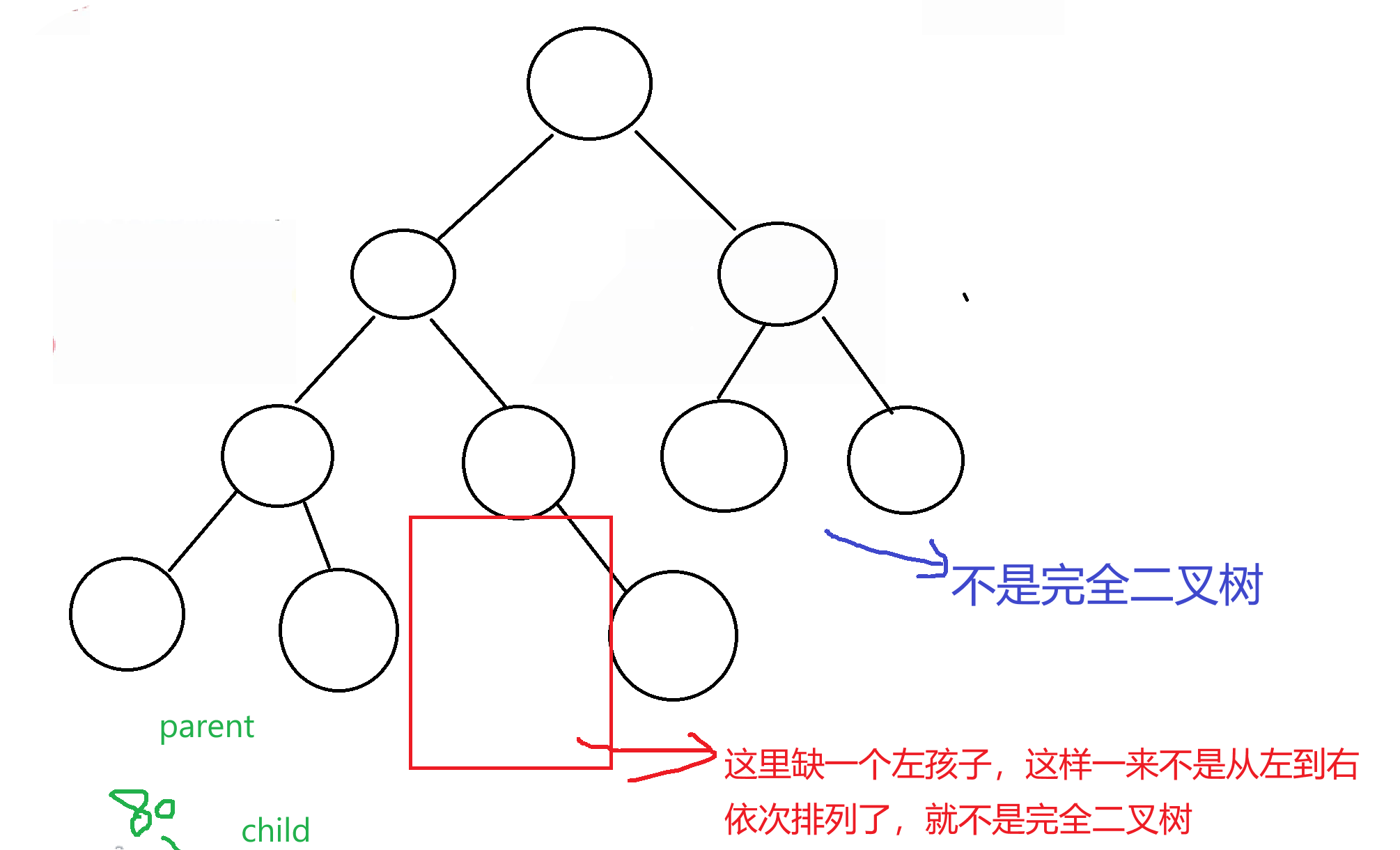
缺一个左孩子,这样一来不是从左到右依次排列了,就不是完全二叉树
二叉树的性质:

三、二叉树的存储结构
二叉树一般可以使用二中存储结构,一种顺序结构,一种链式结构
3.1 顺序结构
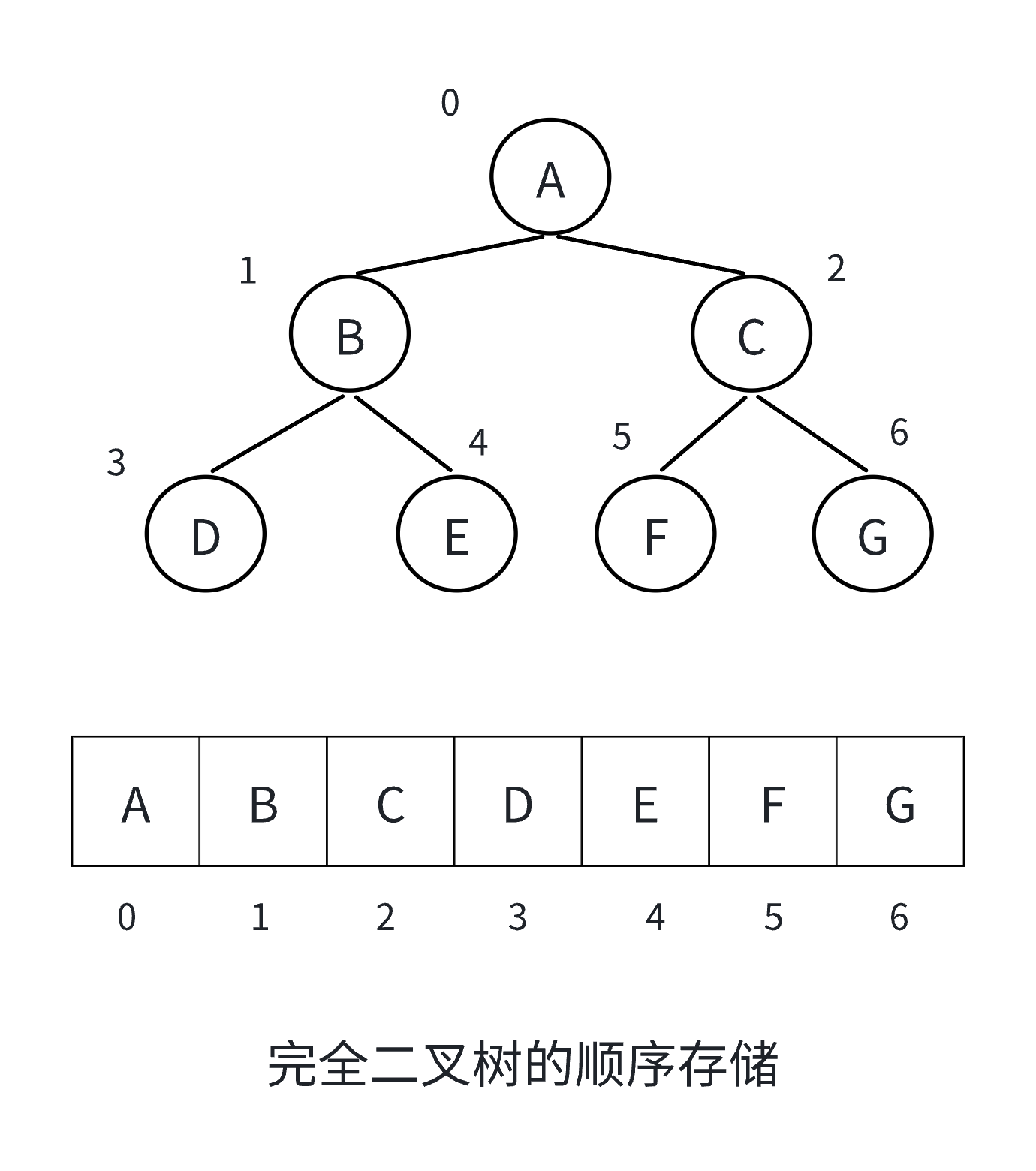
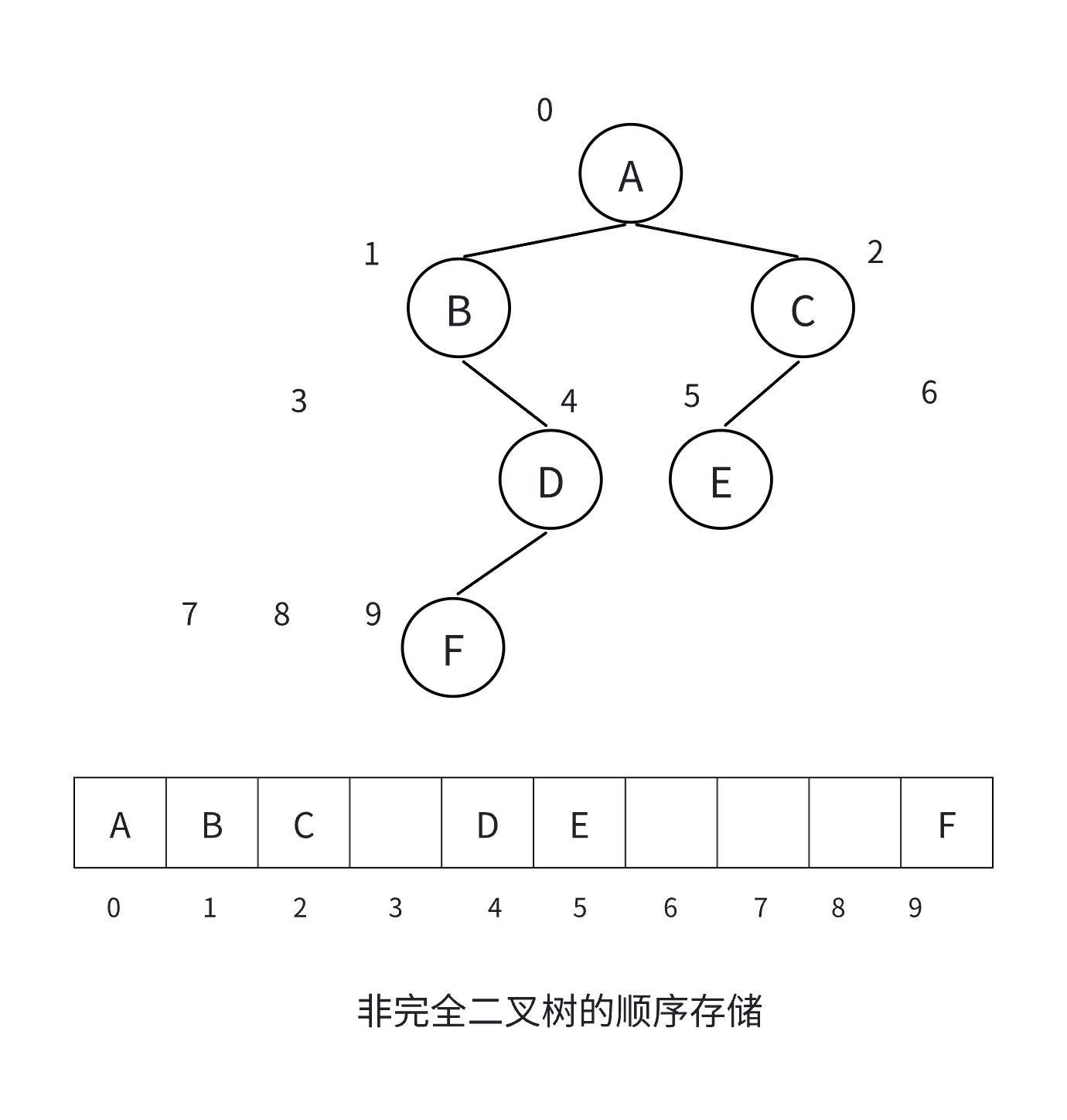
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树会有空间的浪费,完全二叉树更适合使用顺序结构存储。
我们通常把堆(一种二叉树)使用顺序结构的数组来存储,需要注意的是这里的堆和操作系统虚拟进程地址空间中的堆是两回事,一个是数据结构,一个是操作系统中管理内存的一块区域分段
 链表结构
链表结构
3.2 链式结构
二叉树的链式存储结构是指用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。
通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址。
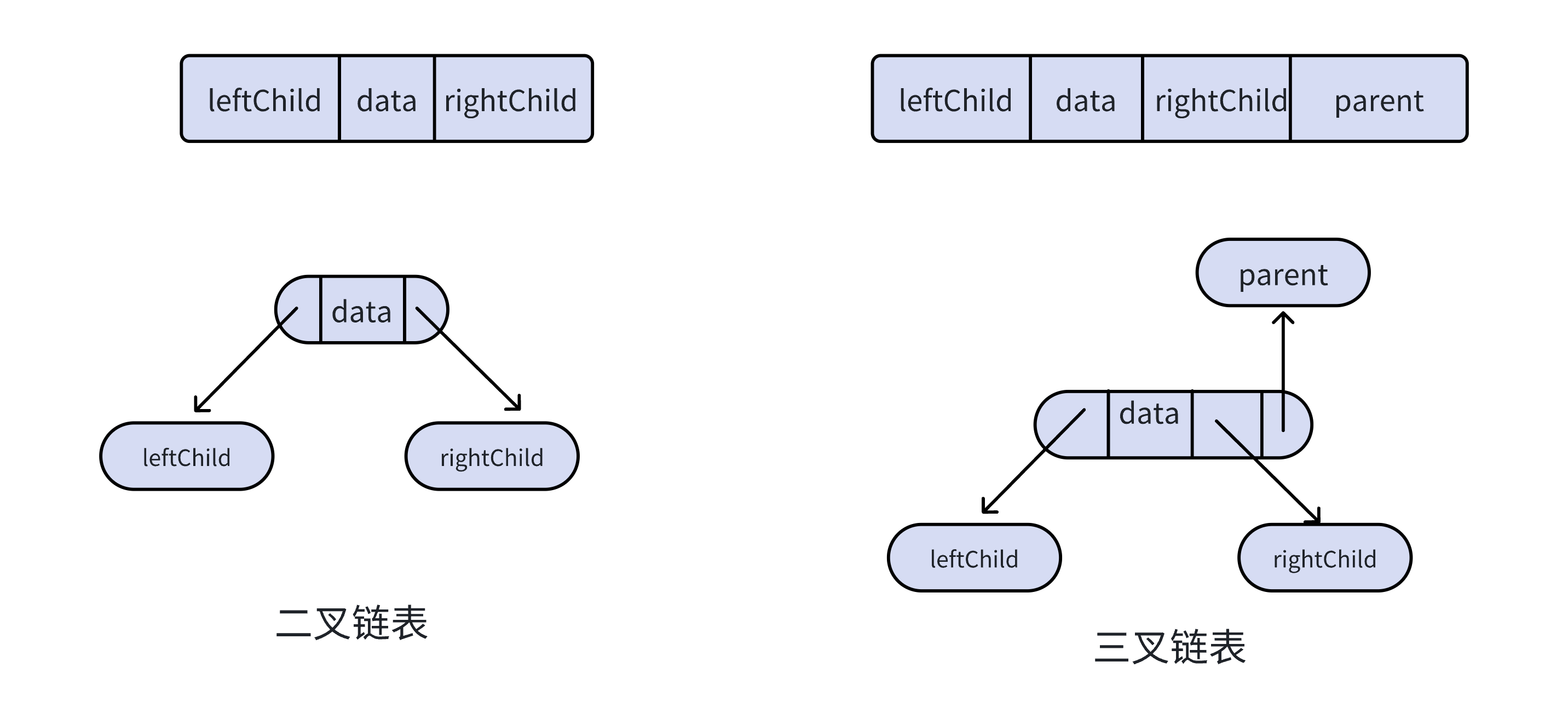
链式结构又分为二叉链和三叉链,当前我们学习中⼀般都是二叉链。后面的学习中会学到高阶数据结构如红黑树等会用到三叉链。
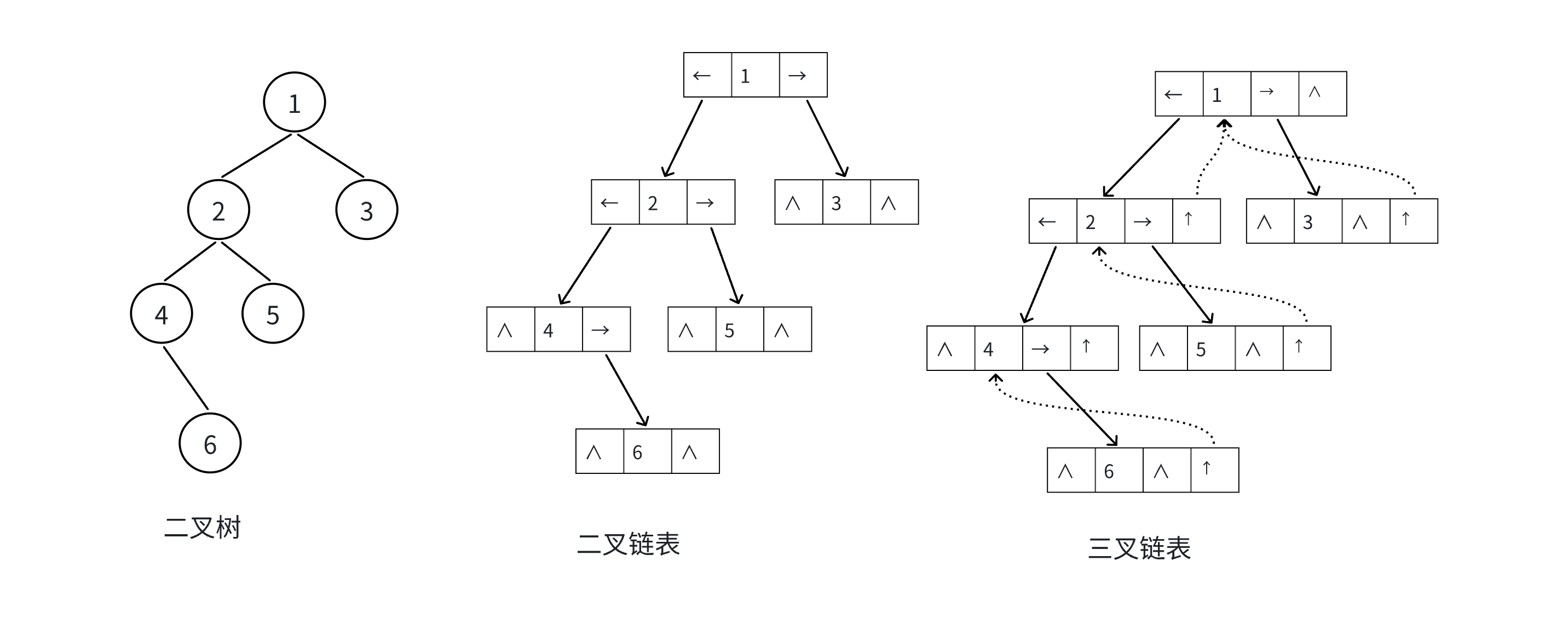

)
:GPIO 输入之光敏传感器控制蜂鸣器)








:雨骑古莲村游记)

TCP拥塞控制与拥塞控制算法深度剖析)
)



![矿物分类系统开发笔记(二):模型训练[删除空缺行]](http://pic.xiahunao.cn/矿物分类系统开发笔记(二):模型训练[删除空缺行])

