基于偏最小二乘法（PLS）多输入单输出的回归预测【MATLAB】

在科学研究和工程实践中，我们常常需要根据多个相关变量来预测一个关键结果。例如，根据气温、湿度、风速等多个气象因素预测空气质量指数，或根据多种原材料成分预测产品的最终性能。这类“多输入单输出”的预测任务，对模型处理复杂变量关系的能力提出了挑战。本文将介绍一种经典且高效的统计建模方法——偏最小二乘法（Partial Least Squares, PLS），并展示如何在MATLAB中利用它实现精准的回归预测。

为什么选择偏最小二乘法（PLS）？

在处理多输入数据时，变量之间往往存在高度相关性（即共线性），或者输入变量的数量远超样本数量，这会使传统回归方法（如多元线性回归）失效或表现不佳。偏最小二乘法正是为解决这类问题而设计的。

PLS的核心优势在于它能够：

• 有效处理共线性：即使输入变量之间高度相关，PLS也能稳定地提取信息，避免模型崩溃。
• 降维与信息融合：它不直接使用原始变量，而是通过分析输入与输出之间的关系，构建出一组新的、互不相关的“综合变量”（也称潜变量或主成分）。这些综合变量集中了原始数据中的关键信息，同时大幅降低了数据的复杂度。
• 兼顾输入与输出的关系：与主成分分析（PCA）只关注输入数据的方差不同，PLS在提取综合变量时，会同时考虑这些变量对输出目标的预测能力，确保降维过程“有的放矢”。

因此，PLS特别适合于变量多、相关性强、样本量有限的复杂预测场景。

PLS的工作原理（直观理解）

可以将PLS的运作过程想象成一场“信息提炼”之旅：

1. 寻找最佳“投影方向”：PLS首先在输入数据中寻找一个方向，使得沿着这个方向投影后得到的“综合变量”，既能最大程度地概括输入数据的变化，又能最好地解释输出变量的变化。
2. 提取第一对“潜变量”：根据找到的方向，计算出输入数据的第一个“综合变量”和对应的输出“综合变量”。这两个变量共同捕捉了数据中最核心的预测信息。
3. 剥离已提取信息：将原始数据中已经被这对“潜变量”解释的部分剔除，得到“残差数据”。
4. 重复过程：在残差数据上重复上述步骤，寻找下一个最佳方向，提取第二对潜变量。这个过程可以持续进行，直到提取出足够数量的潜变量，或者模型性能不再显著提升。
5. 建立预测模型：最终，PLS将这些潜变量与原始输出变量建立回归关系。当有新的输入数据时，模型会先将其转换为对应的潜变量，再通过回归方程预测出最终的输出结果。

整个过程自动化地完成了从高维、相关数据中提取关键预测因子，并建立简洁高效模型的任务。

MATLAB实现步骤

在MATLAB中实现PLS回归预测非常便捷，主要依赖其内置的统计和机器学习工具。以下是关键步骤：

1. 数据准备：

   • 使用 readtable 或 xlsread 等函数加载数据。
   • 将数据划分为训练集和测试集（可使用 cvpartition）。
   • 对输入和输出数据进行归一化处理（mapminmax 函数），这是PLS的标准预处理步骤。

2. 模型训练：

   • 调用 plsregress 函数，输入训练集的输入矩阵和输出向量。
   • 指定需要提取的潜变量数量。这个数量可以通过交叉验证（Cross-Validation）来确定，以避免过拟合。plsregress 函数会返回模型系数、得分、载荷等关键信息。

3. 模型验证与潜变量选择：

   • 利用交叉验证结果，绘制预测误差随潜变量数量变化的曲线。
   • 选择误差最小或趋于稳定的潜变量数量，作为最终模型的配置。

4. 预测与评估：

   • 使用训练好的模型对测试集进行预测。
   • 计算预测性能指标，如决定系数（R²）、均方根误差（RMSE）等，评估模型的准确性。
   • 使用 plot 函数绘制预测值 vs. 真实值的散点图，直观检验模型效果。

应用场景

偏最小二乘法在众多领域都有广泛应用：

• 化学与制药：光谱数据分析（如近红外、拉曼光谱），根据光谱特征预测物质浓度或成分。
• 生物医学：基因表达数据分析，预测疾病状态或治疗反应。
• 工业过程控制：根据多个传感器读数预测关键产品质量指标。
• 社会科学：分析调查问卷数据，预测用户满意度或行为倾向。

优势与注意事项

优势：

• 算法成熟稳定，理论基础扎实。
• 特别擅长处理小样本、多变量、高共线性的数据。
• 模型具有较好的可解释性，可通过载荷分析了解各输入变量的重要性。

注意事项：

• 数据标准化是必要步骤。
• 潜变量数量的选择至关重要，需通过交叉验证等方法谨慎确定。
• 主要适用于线性或近似线性关系；对于强非线性问题，可考虑结合核方法或其他非线性模型。

结语

偏最小二乘法（PLS）作为一种强大的多变量分析工具，在多输入单输出回归预测任务中表现出色。它巧妙地解决了高维数据带来的共线性和维度灾难问题，通过提取关键潜变量，构建出简洁而高效的预测模型。借助MATLAB强大的数据处理和统计分析功能，研究人员和工程师可以轻松实现PLS模型，快速从复杂数据中挖掘价值，为科学决策和工程优化提供有力支持。无论是初学者还是资深从业者，PLS都是一项值得掌握的重要技能。

部分代码

%% 清空环境
warning off;          % 关闭警告提示
clc;                  % 清空命令行
clear;                % 清除工作区变量
close all;            % 关闭所有图形窗口%% 读取数据
res = xlsread('data.xlsx');  % 假设最后一列为输出（标签），其余为输入（特征）
fprintf('数据已加载，共 %d 个样本，%d 个特征。\n', size(res,1), size(res,2)-1);%% 划分训练集和测试集
train_ratio = 0.7;            % 训练集占比
n = size(res, 1);             % 总样本数
trainnum = floor(train_ratio * n);  % 训练样本数量
idx = randperm(n);            % 随机打乱索引% 提取训练集（输入 P，输出 T），并转置为 【特征×样本】格式
P_train = res(idx(1:trainnum), 1:end-1)';  % 输入：前若干列为特征
T_train = res(idx(1:trainnum), end)';      % 输出：最后一列为目标值
M = size(P_train, 2);                      % 训练样本个数% 提取测试集
P_test = res(idx(trainnum+1:end), 1:end-1)'; % 测试输入
T_test = res(idx(trainnum+1:end), end)';     % 测试输出
N = size(P_test, 2);                         % 测试样本个数fprintf('训练集大小: %d 个样本\n', M);
fprintf('测试集大小: %d 个样本\n', N);%% 数据归一化 [0,1]
% 对输入和输出分别进行归一化，并保存参数用于反归一化
[p_train, ps_input] = mapminmax(P_train, 0, 1);
p_test = mapminmax('apply', P_test, ps_input);[t_train, ps_output] = mapminmax(T_train, 0, 1);
t_test = mapminmax('apply', T_test, ps_output);% 转置为【样本×特征】格式，适配 plsregress 函数输入要求
p_train = p_train';
p_test  = p_test';
t_train = t_train';
t_test  = t_test';

运行结果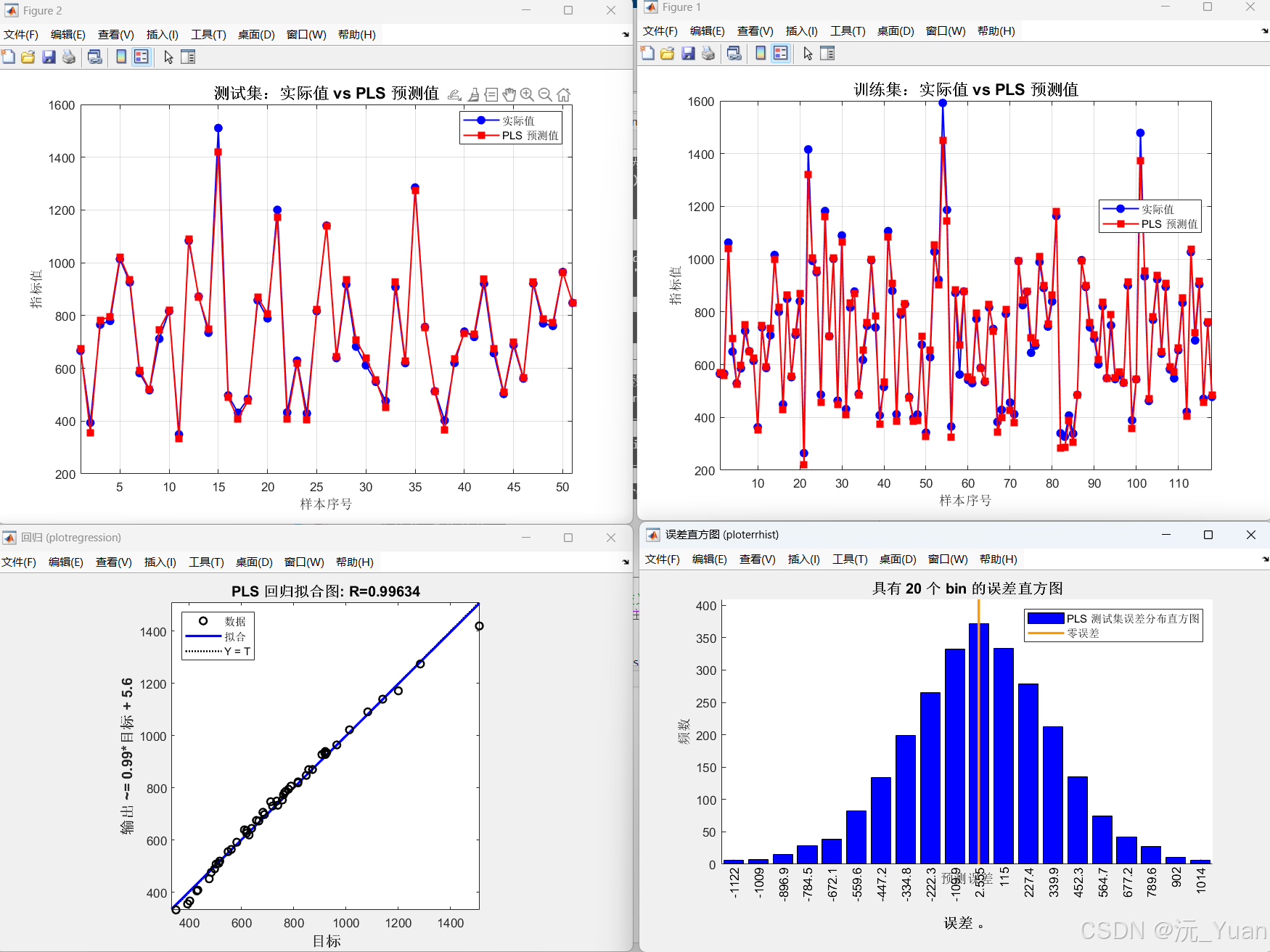

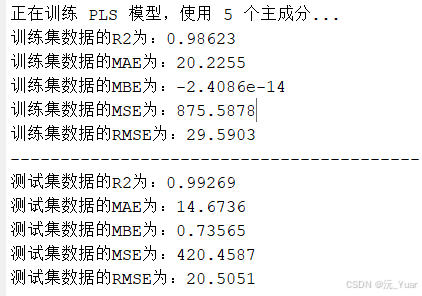
代码下载

https://mbd.pub/o/bread/YZWXlJhvaA==