
在深度学习中,神经网络的初始化是一个看似不起眼,却极其重要的环节。它就像是一场漫长旅程的起点,起点的选择是否恰当,往往决定了整个旅程的顺利程度。
今天,就让我们一起深入探讨神经网络初始化的数学策略,以及这些策略对训练的影响。
一、为什么要初始化?
当我们搭建好神经网络模型,准备开启训练之旅时,权重和偏置的初始值就像是模型的“起跑线”。
如果起跑线设置得不合理,模型可能会陷入“跑不动”或者“跑偏”的困境。
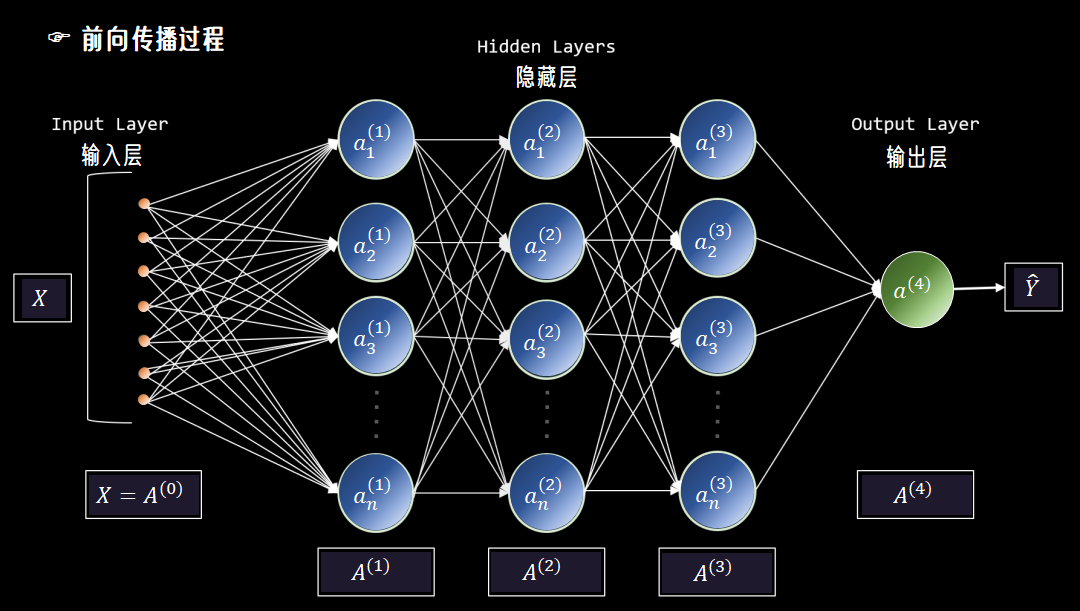
比如,如果所有权重都初始化为零。那么无论输入是什么,每一层的输出都会是相同的值,网络的梯度也会消失,模型根本无法学习。
0m×n=(00⋯000⋯0⋮⋮⋱⋮00⋯0)\mathbf{0}_{m \times n} = \begin{pmatrix} 0 & 0 & \cdots & 0 \\ 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 0 \end{pmatrix}0m×n=00⋮000⋮0⋯⋯⋱⋯00⋮0
而如果权重初始化过大,又会导致梯度爆炸,让模型的训练过程变得混乱不堪。
因此,合理的初始化是神经网络训练能够顺利进行的关键第一步。它不仅影响模型的收敛速度,还决定了模型是否能够收敛到一个好的解。
二、权重初始化的方法
权重初始化是深度学习中一个重要的步骤,它对模型的收敛速度和最终性能有显著影响。
以下是一些常见的权重初始化方法及其数学原理:
2.1 随机初始化
随机初始化是最直观的一种方法。它的核心思想是给每个权重赋予一个随机值,从而打破神经元之间的对称性。
数学上,我们通常会从一个均匀分布或正态分布中随机抽取权重值。
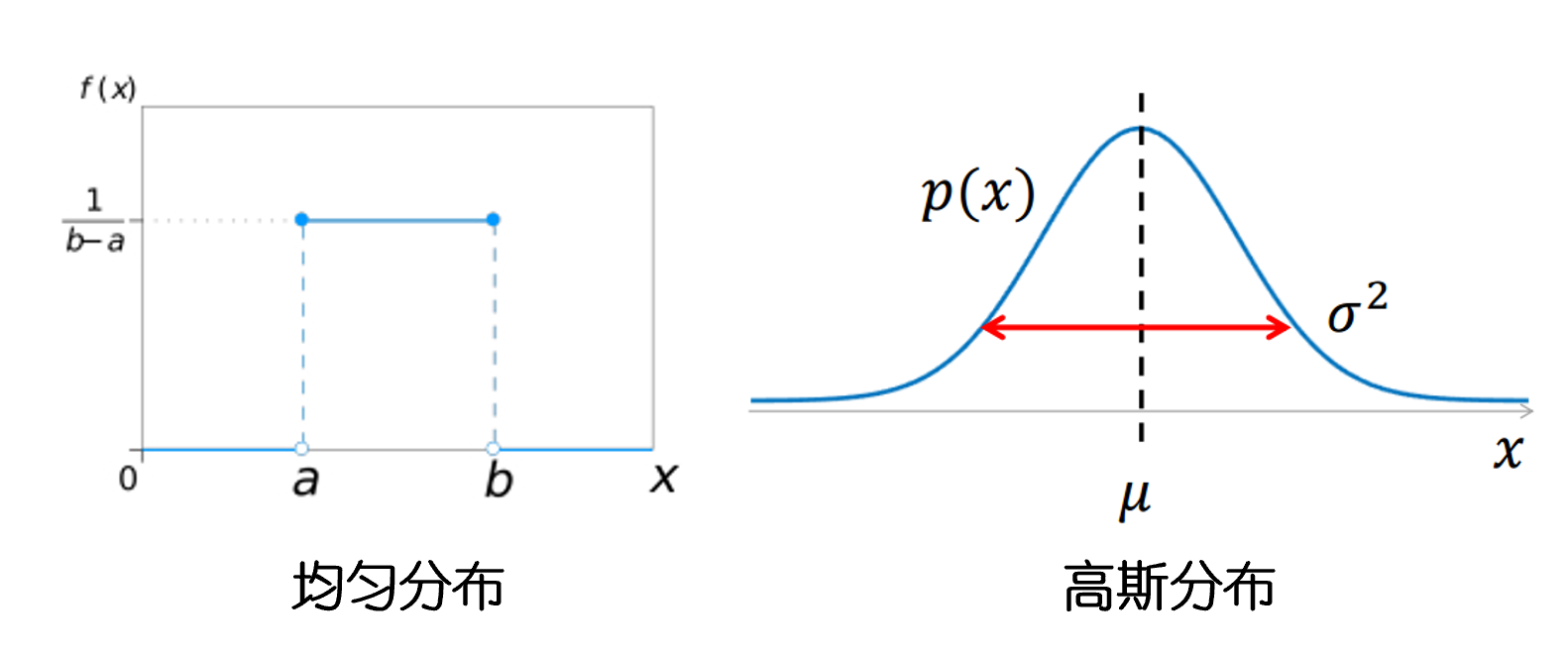
例如,我们可以使用均匀分布 U[−ϵ,ϵ]U[-\epsilon, \epsilon]U[−ϵ,ϵ],其中 ϵ\epsilonϵ 是一个很小的正数。<>
这样做的好处是简单直接,能够让神经元在初始阶段就具有不同的激活值,从而避免了“所有神经元都一样”的问题。
但如果ϵ\epsilonϵ选择得过大或过小,可能会导致网络在训练初期就出现梯度爆炸或梯度消失的问题。因此,我们需要还更精细的初始化方法。
2.2 Xavier初始化
Xavier初始化是一种针对激活函数为Sigmoid或Tanh的网络设计的初始化方法。其核心思想是保持输入和输出的方差一致,从而避免梯度消失或爆炸。
假设输入的方差为 Var(x)\text{Var}(x)Var(x),权重的方差为 Var(w)\text{Var}(w)Var(w),那么对于一个神经元的输出 y=w⋅xy = w \cdot xy=w⋅x,其方差可以表示为:
Var(y)=Var(w)⋅Var(x)\text{Var}(y) = \text{Var}(w) \cdot \text{Var}(x)Var(y)=Var(w)⋅Var(x)
为了保持输入和输出的方差一致,我们需要让 Var(y)=Var(x)\text{Var}(y) = \text{Var}(x)Var(y)=Var(x)。因此,Xavier初始化将权重的方差设置为:
Var(w)=1n\text{Var}(w) = \frac{1}{n}Var(w)=n1
其中 nnn 是前一层的神经元数量。
这样,无论网络有多深,每一层的方差都能保持一致,也就避免了梯度消失或爆炸的问题。
2.3 He初始化
He初始化是一种针对ReLU激活函数设计的初始化方法。
He初始化的核心思想是调整权重的方差,使其更适合ReLU激活函数。
具体来说,He初始化将权重的方差设置为:
Var(w)=2n\text{Var}(w) = \frac{2}{n}Var(w)=n2
其中nnn仍然是前一层的神经元数量。
这个公式比Xavier初始化多了一个2,是因为ReLU激活函数在训练初期更容易产生较大的梯度。通过这种方式,He初始化能够更好地平衡ReLU激活函数的特性,避免梯度爆炸的问题。
三、偏置初始化的策略
与权重初始化相比,偏置初始化相对简单一些。一般来说,偏置可以初始化为零或一个很小的常数。
在大多数情况下,将偏置初始化为零已经足够了。然而,对于某些特定的激活函数,如ReLU,将偏置初始化为一个很小的正数可能会更有帮助。
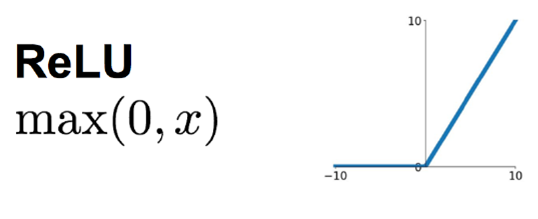
这是因为ReLU激活函数在输入为负时输出为0,这可能会导致一些神经元在训练初期就“死亡”,即它们的输出始终为0。
通过将偏置初始化为一个很小的正数,可以增加神经元的初始输出,从而避免它们过早死亡。
神经网络的初始化是一个看似简单却极其重要的环节。通过精心设计权重和偏置的初始化策略,我们可以有效地避免梯度消失或爆炸的问题,从而让网络在训练过程中能够快速收敛,并且具有更好的稳定性。
在实际应用中,我们需要根据网络的结构和激活函数的特性,选择合适的初始化方法。例如,对于使用Sigmoid或Tanh激活函数的网络,Xavier初始化是一个不错的选择;而对于使用ReLU激活函数的网络,He初始化则更为合适。
注:本文中未声明的图片均来源于互联网




![[rStar] 搜索代理(MCTS/束搜索)](http://pic.xiahunao.cn/[rStar] 搜索代理(MCTS/束搜索))



)





 D题题解记录)




