深度神经网络由多层网络连接而成，网络连接处防止线性直接相关，采用非线性函数进行逐层隔离，真正实现每层参数的独立性，也就是只对本层提取到的特征紧密相关。因为如果是线性函数直接相连就成了一层中间网络了，只不过参数之间做变换，失去了深度学习的意义。
1.非线性函数的意义

        每一层可以联想为一组正交基，可以理解成一个平面，平面通过非线性变换达到扭曲逼近拟合真实要求的曲面。这是基于目前通常的思路，一个平面上y=Wx +B变换后，再通过非线性进行扭曲成y=x*sin(x)(效果举例，不是真正就是这个函数).实现了逐层扭曲直至达到最终要求。

         可不可以抛开第一步的正交基，直接用非平面内的非线性曲面来拟合本层任务的扭曲要求，有待进一步探索。

2.损失函数

        输入数据->深度网络模型->输出数据，在这个数据流向里，数据最终经过n层网络的处理后，也就是多个函数变换后（有线性、也有非线性）得到一个输出值（不是数量1个），怎么判断输出值是不是我们想要的？那就是离真实值越接近越好。最直观的就是loss = |f(x)-y|,loss值太大后，我们要求反向逐层调整W,B的值，直至loss值比较小为止。

下面单独讲损失函数。

L1 LOSS 

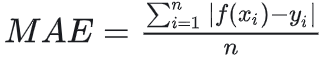
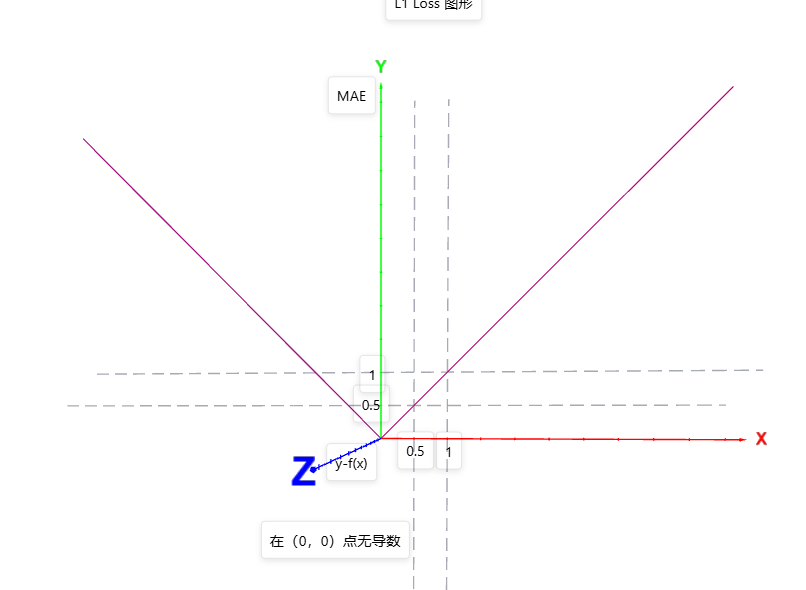
图中很明显在（0，0）点无导数，在其他位置导数是常数。优点是：导数常量不会梯度爆炸，就是不出现极大值。

L2 loss

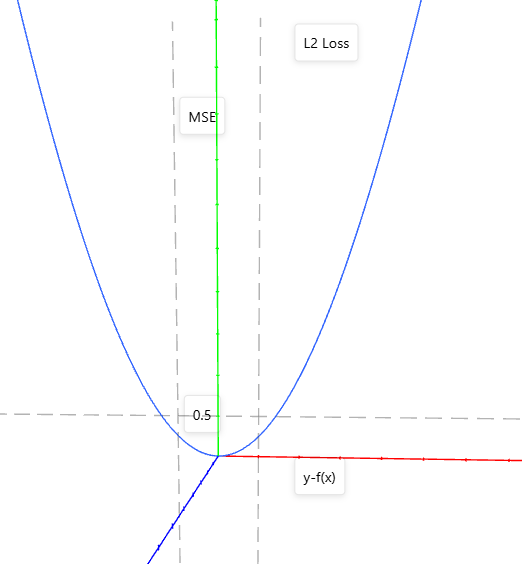
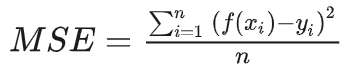
也就是f=x*x的函数图形。

优点：函数曲线连续，处处可导，随着误差值的减小，梯度也减小，有利于收敛到最小值。缺点：当函数的输入值距离中心值较远的时候，使用梯度下降法求解的时候梯度很大，可能造成梯度爆炸。

3.Smooth L1 loss

公式如下：

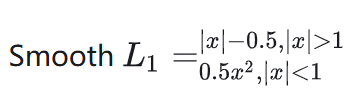
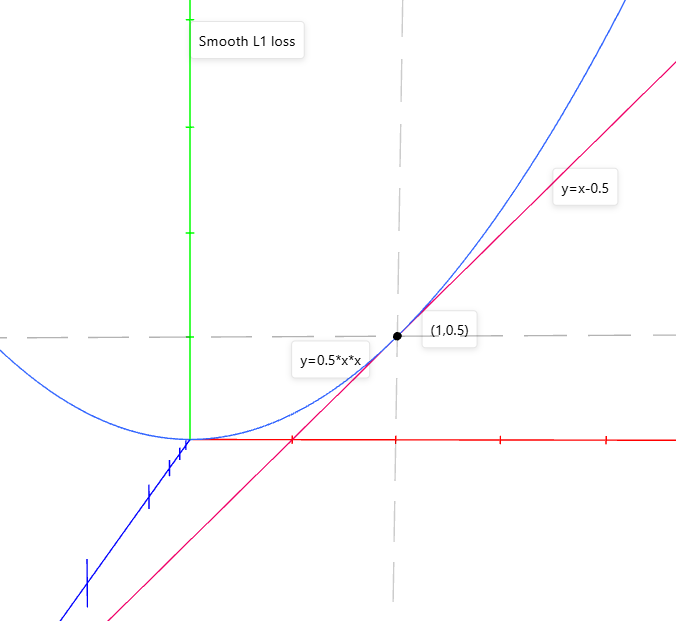
Smooth L1 loss 结合了L1和L2的优点，高偏差时采用固定梯度防梯度爆炸，靠近精度需求时，采用可导方式，有效调参。