数据结构之克鲁斯卡尔算法

前言：和Prim算法一样，Kruskal 算法也是用来生成最小生成树的，这篇文章来学习一下Kruskal算法的实现

一、实现流程

初始化的时候，将所有的边用一个数组存储，并且按权值从小到大进行排序，每次选一个权值最小的边加入到生成树中，但是在加入之前，需要判断加入的这条边会不会使生成树形成环路。接下来我们分步骤看一下算法的执行过程
我们来看这样一个图
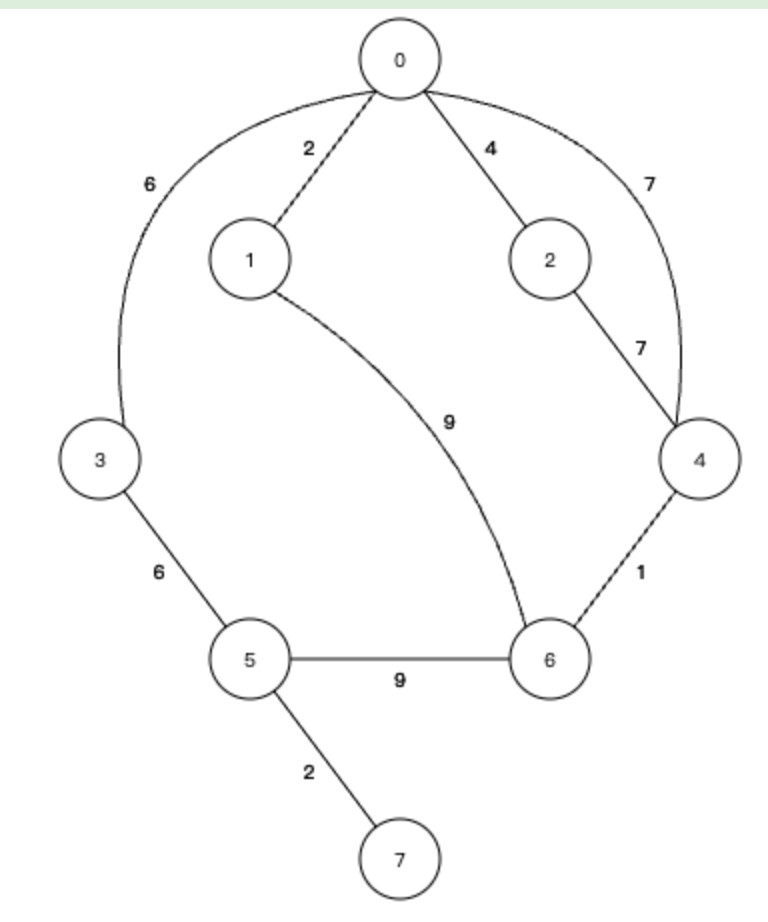
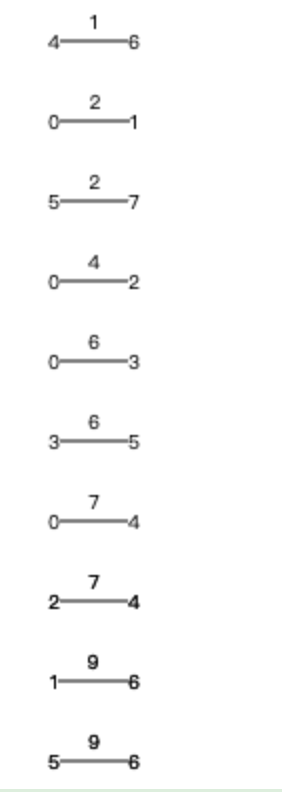
在这里插入图片描述
1、边数组初始化
从小到大存储边

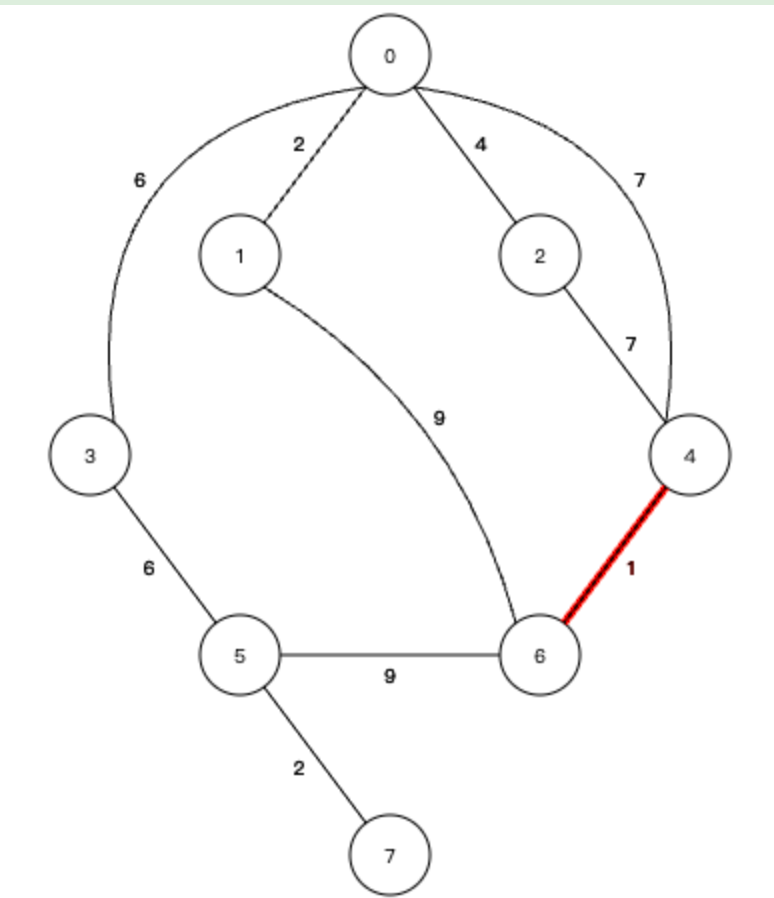
2、权值最小，为1的边连接4号节点和6号节点，这两个节点不在同一棵树中，不会形成环路，因此加入生成树
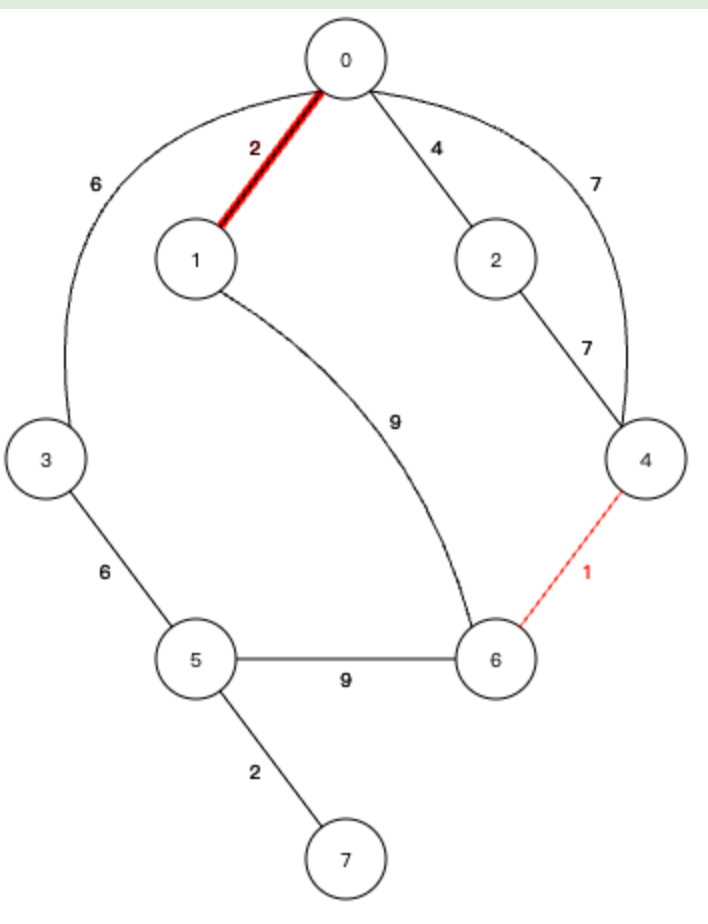
在这里插入图片描述
3、下一个权值最小的边，0-2 ，权值为2，这个边及加入生成树也不会形成环路，所以加入生成树

4、下一个权值最小的边是 5-7，同上也直接加入树

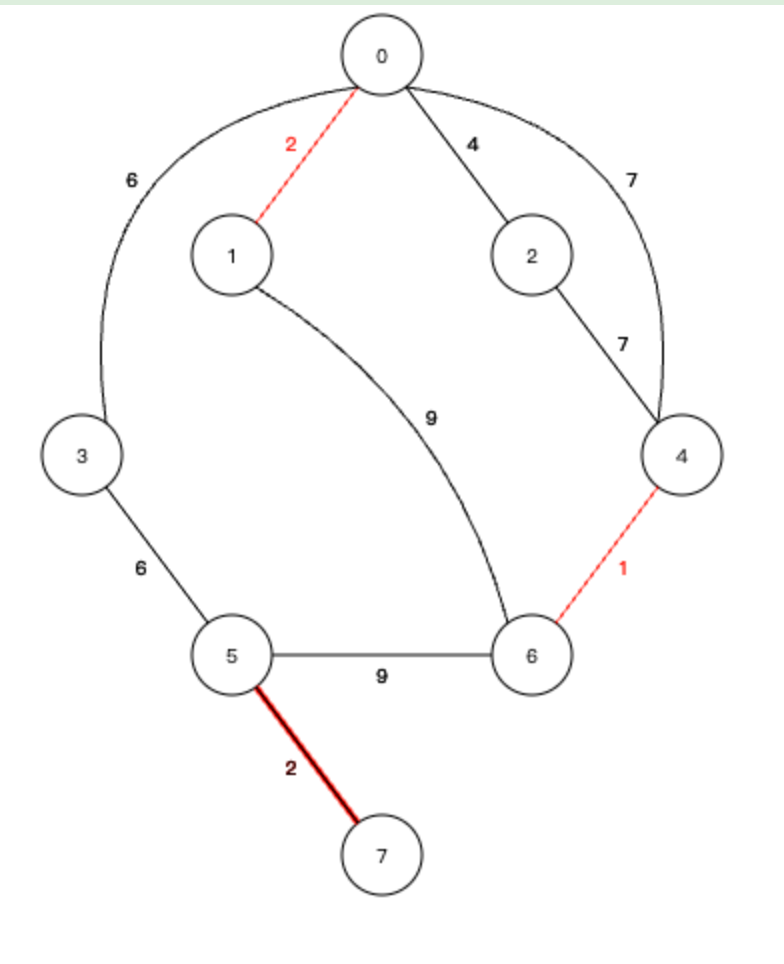
5、下一个边 0-2，同样加入生成树

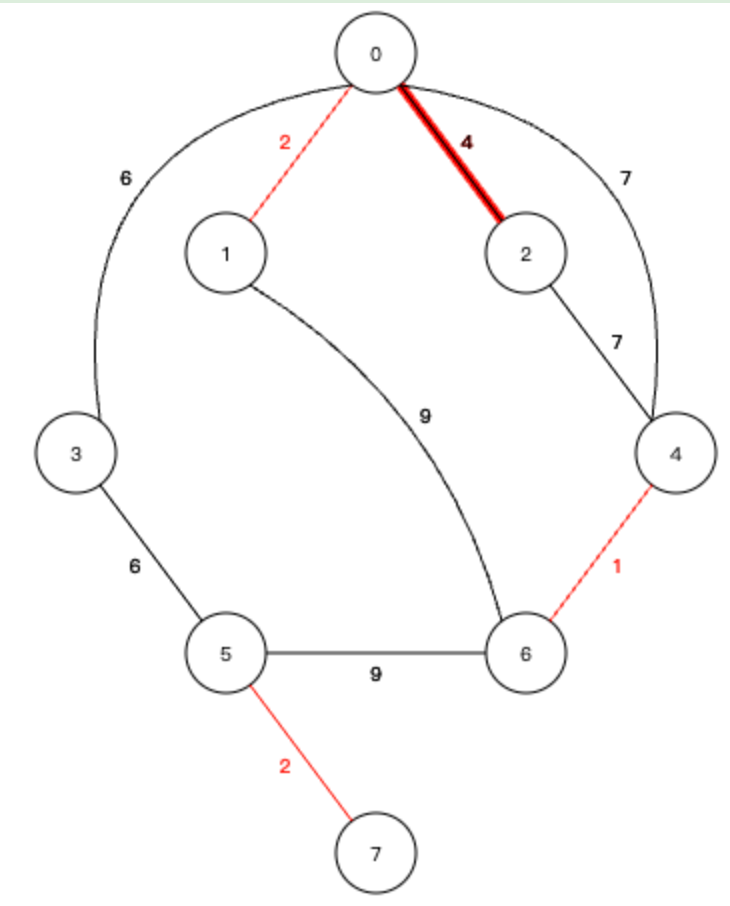
6、下一个 0-3 的边，也不会形成环路，加入
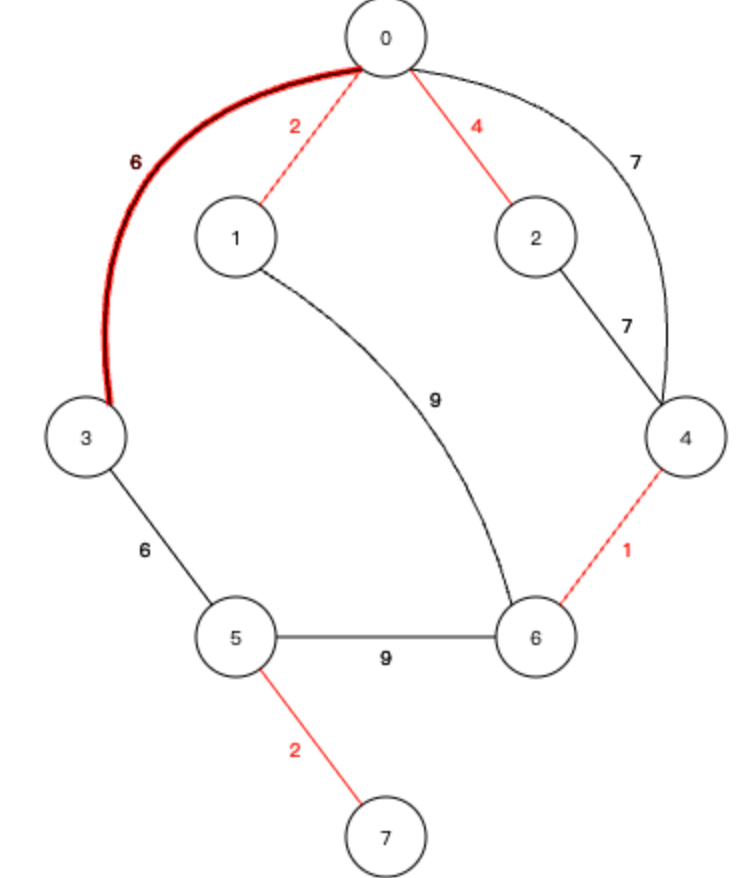
在这里插入图片描述

7、下一个 3-5 的边也可以加入生成树
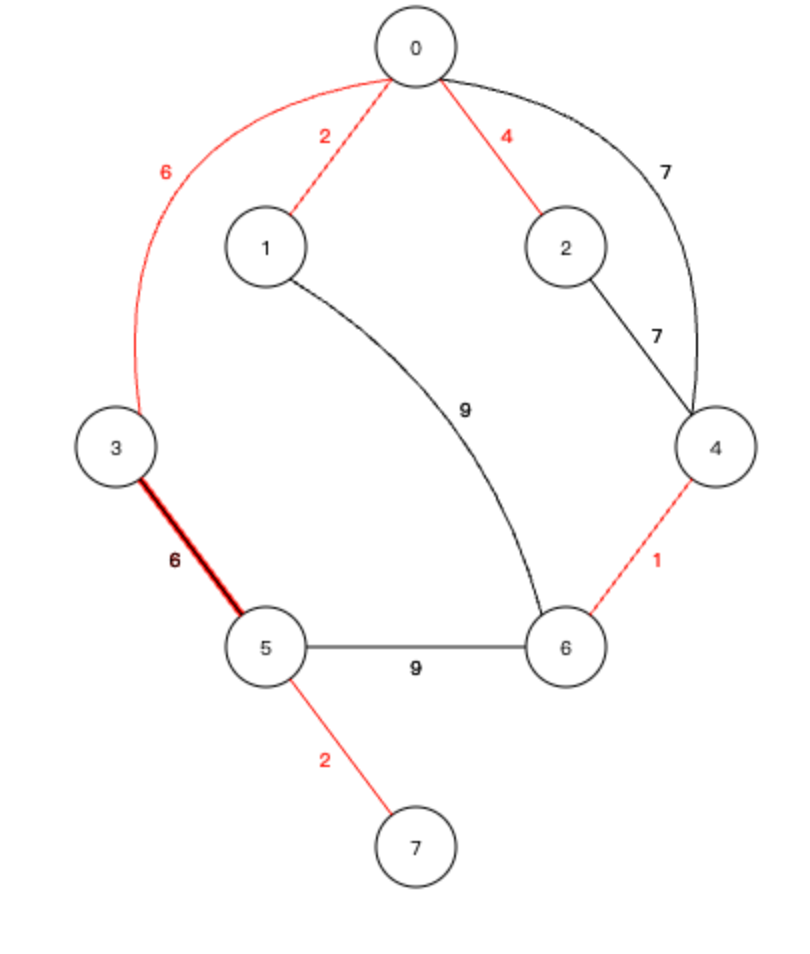
在这里插入图片描述

8、下一个 0-4 ，也可以直接加入
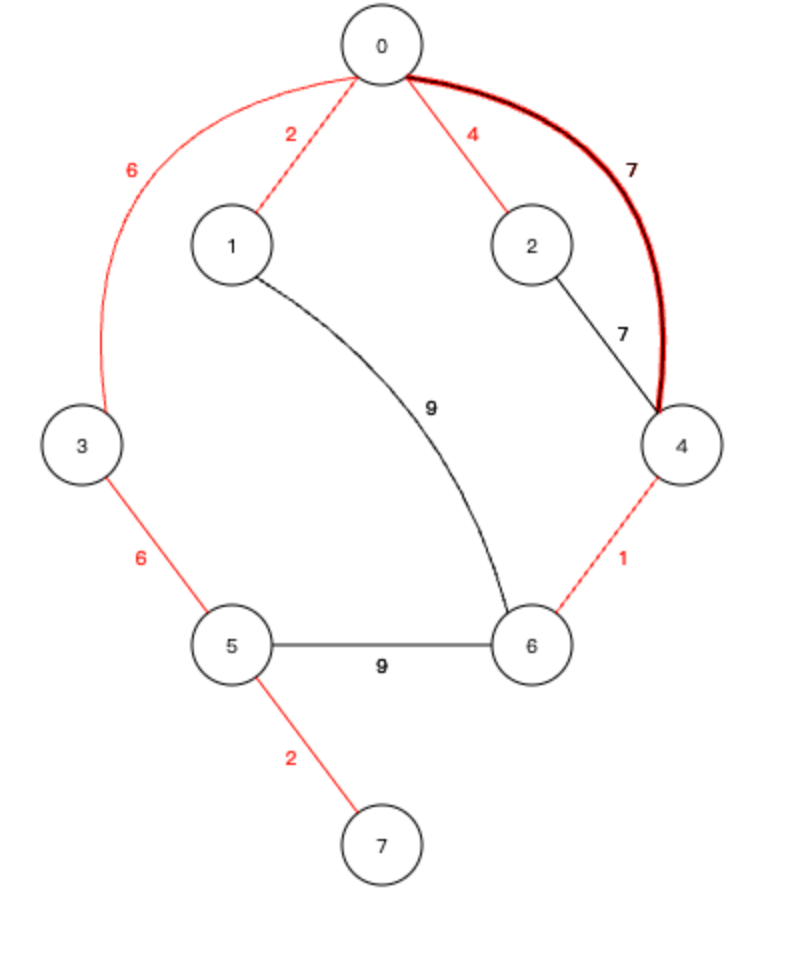
在这里插入图片描述

9、至此，所有的节点已经全部加入到生成树中，算法结束

二、代码实现

1、定义常数

#define MaxSize 100
#define MaxEdge 200  // 最大边数
#define MaxVex 100   // 最大顶点数

2、结构体

需要两个结构体，一个是图，一个是边
图需要包括点的个数，边的个数，和邻接矩阵

typedef struct {int vexnum;  // 顶点数int arcnum;  // 边数int arcs[MaxVex][MaxVex];  // 邻接矩阵
} MGraph;

边的结构体需要包含边的两个顶点，和边的权值

typedef struct{int a,b; // 边的两个顶点int weight; // 边的权值
} Edge

3、初始化变量和工具函数

需要一个边数组，存储所有的边

Edge edges[MaxEdge]; // 变数组

Kcuscal 算法需要找权值最小的边，所以对所有的边进行排序，c语言中有一个内置的 qsort 方法，可以对任何类型进行排序，接收四个参数：
参数一：void* base，待排数组
参数二：size_t num，待排元素的个数
参数三：size_t size，每个元素的大小，单位为字节，使用 sizeof() 函数获取
参数四：int (*compare)(const void * , const void *)，排序函数
需要一个排序函数 compare，将权值比较小的边放在前面
void * 表示泛型指针类型，表示a可以指向任何类型的数据
(Edge*) 是一个类型转换，由于在入参中我们定义的 a 可以是任何类型的数据，这里使用 (Edge*) 将a转换为指向 Edge 结构体的指针。
Edge *edgeA 声明了一个新指针，并且将 a 指针的值赋值给它，现在 edgeA 就是一个指向 Edge 结构体的指针。
返回值，如果是负数，表示 edgeA->weight 小，则不更换数据的位置；如果是正数，表示 edgeA->weight 小，则要更换数据的位置。

int compare(const void *a, const void *b){Edge *edgeA = (Edge *) a;Edge *edgeB = (Edge *) b;return edgeA->weight - edgeB->weight;
}

另外判断边是否能够加入到生成树中的时候，需要判断这条边和生成树是不是在同一棵树中，如果在同一棵树中，那么加入这条边，一定会形成环路。我们在合并两个树的时候学过，将一个树 A 合并到另一棵树 B 中，就是将树的根节点 A 的父节点更新成另一棵树的根节点 B。
所以我们需要维护一个数组 parent，来存储所有的节点的父节点，初始化的时候，都初始化为-1

int parent[MaxVex]; // 根节点数组（并查集）

节点当加入到生成树中就需要进行合并操作，需要更新节点对应的根节点。
所以我们需要一个查找根节点的函数 Find，来查找一个节点所在的树的根节点
如果 parent[x] 小于 0 ，说明当前节点还没有加入到生成树中，就直接返回节点本身。如果parent[x] 大于 0，则向上找父节点，直到找到 parent[x] 小于 0 的的点。

// 并查集的Find操作
int Find(int *parent,int x){while(parent[x]>=0) x=parent[x]; // 循环向上寻找下标为x顶点的根return x; // while循环结束时找到了根的下标
}

4、主函数

在主函数中需要做的事情：
1、给边数组 edges 按权值排序
2、初始化 parent 数组为 -1
3、遍历边，找边的两个顶点的 parent，如果 parent 不相同，表示两个顶点不在同棵树中，则将其中一个顶点的 parent 指向另一个顶点，也就是将两个顶点合并在一棵树中

void MiniSpanTree_Kruskal(Gragh G){int i,n,m;// edges 排序qsort(edges, G.arcnum, sizeof(Edge), compare);// 初始化parentfor(i=0;i<G.vexnum;i++) parent[i] = -1;// 遍历所有边for(i=0;i<G.arcnum;i++){n = Find(edges[i].a);  // 第一个节点所在的树的根节点m = Find(edges[i].b);  // 第二个节点所在的树的根节点if(n!=m){  // 根节点不同，说明这两个节点位于两棵不同的树，则合并这两棵树parent[n] = m;printf("(%d->%d) 权值:%d\n", edges[i].a, edges[i].b, edges[i].weight);}}
}

三、和Prim算法的对比

组成树的元素有两个，一个是节点，一个是边。Prim 算法主要关注节点，找和当前的最小生成树距离最近的节点，把节点加入到生成树中。而Kruskal算法主要关注的是边，先将所有的边排序，将权值最小并且不会形成环路的边依次加入到生成树中。由于Kruskal算法要对边进行对比排序，所以Kruskal算法的执行效率取决于边的多少，适合边少的图，我们叫做稀疏图。而Prim算法主要关注节点，适合边多的图（边多就相当于节点少了），我们叫做稠密图。
下面我们来分析一下时间复杂度，假设图的节点数为 v ，边数为 e，
Prim 算法需要执行两层循环，每层执行的次数都是 v，所以Prim算法的时间复杂度是 O(v^2)。
Kruckal 算法 qsort()方法的时间复杂度是 O(elog2e)，它是时间复杂度最高的方法，
外层需要遍历所有的边，时间复杂度是 O(e)， Find 方法的并查集操作的时间复杂度可以优化到很小，可以忽略，所以整个算法的时间复杂度是 O(elog2e)

四、测试代码

在 main 函数中，需要初始化 edges 数组

// 克鲁斯卡尔算法
// 求最小生成树的算法
#include <stdio.h>
#include <stdlib.h>#define MaxSize 100
#define MaxEdge 200  // 最大边数
#define MaxVex 100   // 最大顶点数// 图的邻接矩阵表示
typedef struct {int vexnum;  // 顶点数int arcnum;  // 边数int arcs[MaxVex][MaxVex];  // 邻接矩阵
} MGraph;typedef struct {int a,b; // 边的两个顶点int weight; // 边的权值
}Edge;// 并查集的Find操作
int Find(int *parent,int x){while(parent[x]>=0) x=parent[x]; // 循环向上寻找下标为x顶点的根return x; // while循环结束时找到了根的下标
}// 比较函数，用于qsort排序
// const 放在*的左边，表示指针指向的数据不可变，但是指针的指向可变
int compare(const void *a, const void *b) {Edge *edgeA = (Edge*)a;Edge *edgeB = (Edge*)b;return edgeA->weight - edgeB->weight; // 按权值从小到大排序
}Edge edges[MaxEdge]; // 边数组
int parent[MaxVex]; // 父亲顶点数组（并查集）void MiniSpanTree_Kruskal(MGraph G){int i,n,m;// printf("\n排序前的边数组：\n");// for(i=0; i<G.arcnum; i++) {//     printf("(%d-%d) 权值:%d\n", edges[i].a, edges[i].b, edges[i].weight);// }// 按权值由小到大对边排列qsort(edges, G.arcnum, sizeof(Edge), compare);// printf("\n按权值排序后的边数组：\n");// for(i=0; i<G.arcnum; i++) {//     printf("(%d-%d) 权值:%d\n", edges[i].a, edges[i].b, edges[i].weight);// }for(i=0;i<G.vexnum;i++) parent[i]=-1; // 初始化并查集// printf("\n最小生成树的边：\n");for(i=0;i<G.arcnum;i++){ // 遍历每一条边n=Find(parent,edges[i].a); // n是这条边的第一个顶点的根节点所在的下标m=Find(parent,edges[i].b); // m是这条边的第二个顶点的根节点所在的下标if(n!=m){parent[n] = m; // 并操作printf("(%d->%d) 权值:%d\n", edges[i].a, edges[i].b, edges[i].weight);}}
}// 初始化图的边
void initGraph(MGraph *G) {// 示例图：6个顶点，9条边G->vexnum = 6;  // 顶点数 0-5G->arcnum = 9;  // 边数// 手动添加边的信息到edges数组// 顶点0-1，权值4edges[0].a = 0; edges[0].b = 1; edges[0].weight = 4;// 顶点0-2，权值6edges[1].a = 0; edges[1].b = 2; edges[1].weight = 6;// 顶点0-3，权值16edges[2].a = 0; edges[2].b = 3; edges[2].weight = 16;// 顶点1-2，权值10edges[3].a = 1; edges[3].b = 2; edges[3].weight = 10;// 顶点1-4，权值7edges[4].a = 1; edges[4].b = 4; edges[4].weight = 7;// 顶点2-3，权值14edges[5].a = 2; edges[5].b = 3; edges[5].weight = 14;// 顶点2-4，权值3edges[6].a = 2; edges[6].b = 4; edges[6].weight = 3;// 顶点2-5，权值8edges[7].a = 2; edges[7].b = 5; edges[7].weight = 8;// 顶点4-5，权值9edges[8].a = 4; edges[8].b = 5; edges[8].weight = 9;
}int main() {MGraph G;// printf("=== 克鲁斯卡尔最小生成树算法演示 ===\n\n");// 初始化图initGraph(&G);// printf("原始图的边信息：\n");// printf("顶点数：%d，边数：%d\n", G.vexnum, G.arcnum);// printf("所有边：\n");// for(int i = 0; i < G.arcnum; i++) {//     printf("(%d-%d) 权值:%d\n", edges[i].a, edges[i].b, edges[i].weight);// }// printf("\n开始执行克鲁斯卡尔算法：\n");// printf("================================\n");// 执行克鲁斯卡尔算法MiniSpanTree_Kruskal(G);// printf("================================\n");// printf("算法执行完成！\n");return 0;
}