傅里叶变换:
运用频域的出发点就是能够将波形从时域变换到频域,用傅里叶变换可以做到这一点。有如下3种傅里叶变换类型:
1.傅里叶积分(FI);
2.离散傅里叶变换(DFT);
3.快速傅里叶变换(FFT)。
傅里叶积分是一种将时域的理想数学表达变换成频域描述的数学技术。例如,若时域中的整个波形只是一个短脉冲,就可用傅里叶积分将它变换到频域中。
傅里叶积分是在整个时间轴上从负无穷大到正无穷大求积分,得到的结果是零频率到正无穷大频率上连续的频域函数。在这个区间内,每个连续的频率点都对应一个幅值。
实际上,时域波形是由一系列离散点组成的,且这些点是在有限的时间范围T内测量得到的。例如,一个时钟波形可能是从0V到1V的这样一个信号,其周期为1ns,即频率为1 GHz。
为了表示时钟的一个周期,可能会用1000个离散的数据点,其中时间间隔为1ps。图2.4所示为时域中1 GHz的时钟波形。
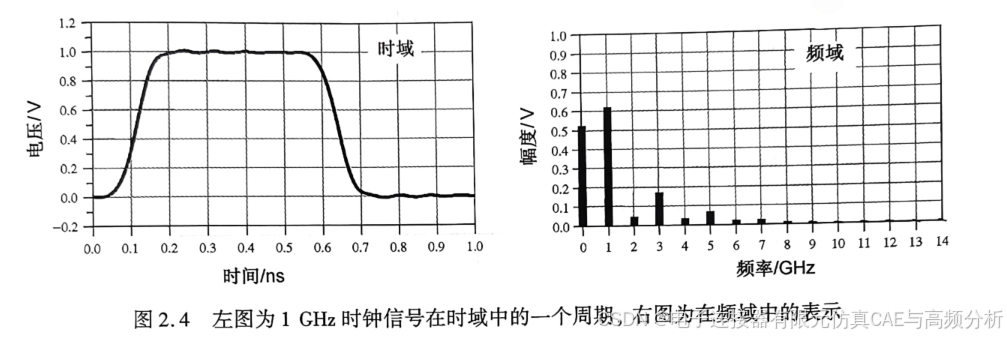
使用离散傅里叶变换可以将这个波形变换到频域中。其中基本的假设就是原始的时域波形是周期的,它每隔T秒重复一次。与积分不同,此处只用到求和,通过简单的数学方法就能将任意一组数据变换到频域中。
最后就是快速傅里叶变换。除了计算每个频率点幅度值的实际算法使用了快速矩阵代数学的技巧,它与离散傅里叶变换是完全一样的。这种快速算法只应用于时域中的数据点个数是2的整幂次的情况,如256点512点或1024点。根据所计算电压点个数的多少,快速傅里叶变换的计算速度比普通离散傅里叶变换可以快100~10000倍。
一般而言,工业界中常常会同时使用傅里叶积分、离散傅里叶变换和快速傅里叶变换这3种方法。现在我们知道这3种算法之间是有区别的,但同时它们又有着同样的用途—将时域波形变换成频域频谱。
提示: 在频域中,对波形的描述变为不同频率正弦波的集合。每个频率分量都有相应的幅度及相位。所有这些频率点及其幅度值的全集称为波形的频谱。
图2.4所示就是一个简单的时域波形,以及用离散傅里叶变换计算得出的频谱图。
每个严肃认真的工程师都应该至少用手工计算一次傅里叶积分来观察它的细节。此后,就无须再手工计算了,可以使用许多商用软件工具完成傅里叶变换,从而更快地得到答案。
许多用法相对简单的商用软件工具都能对输入的任意波形进行离散傅里叶变换或快速傅里叶变换计算。SPICE软件的每个版本都有一个称为.FOUR指令的函数,它可以生成任一个波形前9个频率分量的幅度。更先进的SPICE工具的大多数版本还能用离散傅里叶变换计算全套频率点和幅度值。Microsoft Excel有FFT功能,通常可在“工程插件”中找到。






)
)




)
)




)
