一、什么是中心极限定理？

中心极限定理(Central Limit Theorem, CLT)是概率论与统计学中最重要的定理之一，它揭示了为什么正态分布在自然界和统计学中如此普遍。

​定理表述​：

设X₁, X₂, ..., Xₙ 是一组独立同分布的随机变量序列，它们具有相同的期望值μ和有限的方差σ²。

令样本均值：

则随着样本量n趋向于无穷大，样本均值的标准化形式（啥意思？后面有解释）：

依分布收敛于标准正态分布N(0,1)，即：

​关键要点​：

1. 无论原始分布如何(可以是均匀分布、指数分布、二项分布等)，样本均值的分布都会趋近正态分布
2. 样本量n越大，近似程度越好
3. 标准化过程：(X̄-μ)/(σ/√n) ~ N(0,1)
4. 实际应用中，n>30通常被认为是"足够大"的样本量

二、班级学生身高分析案例

1、案例背景

假设某城市所有10岁学生的平均身高为140cm，标准差为8cm。我们随机抽取36名学生，计算他们的平均身高。那么：

1. 这个样本平均身高的期望值是多少？
2. 样本平均身高的标准差是多少？
3. 样本平均身高在138-142cm之间的概率是多少？

“标准差为8cm”和“样本平均身高的标准差”啥关系？后面解释

---

2、分步计算过程

​步骤1：确定参数​

• 总体均值(μ) = 140cm
• 总体标准差(σ) = 8cm
• 样本量(n) = 36

​步骤2：计算样本均值的期望和标准差​
根据中心极限定理：

• 样本均值的期望 = 总体均值 = 140cm
• 样本均值的标准差(标准误差) = σ/√n = 8/√36 = 8/6 ≈ 1.333cm

​步骤3：标准化区间​
计算138-142cm对应的Z分数：

• 对于138cm：Z = (138-140)/1.333 ≈ -1.5
• 对于142cm：Z = (142-140)/1.333 ≈ +1.5

​步骤4：查标准正态分布表​
P(-1.5 < Z < 1.5) = P(Z < 1.5) - P(Z < -1.5) ≈ 0.9332 - 0.0668 = 0.8664

​结论​：样本平均身高在138-142cm之间的概率约为86.64%。

---

3、可视化理解

想象你是一位老师，每年测量36名学生的平均身高。如果你重复这个过程1000次，这些平均身高的分布会形成一个钟形曲线(正态分布)，中心在140cm，大多数(约86.64%)的结果会落在138-142cm之间。

---

三、生活中的中心极限定理

案例1：餐厅等待时间

一家快餐店单个顾客的服务时间呈右偏分布(大多数顾客很快，少数需要较长时间)。但如果你观察100位顾客的平均服务时间，这个平均时间的分布会接近正态分布。

​为什么？​​

• 单个服务时间：偏态分布
• 平均服务时间(样本量足够大)：正态分布
• 这使得餐厅可以更准确地预测高峰时段的平均等待时间

---

案例2：产品质量控制

工厂生产螺丝钉的长度有微小随机差异。质检部门不检查每个螺丝钉，而是每天随机抽取50个测量平均长度。

​应用CLT​：

• 即使单个螺丝钉长度不是正态分布，平均长度近似正态
• 可以设置合理的控制界限(如±3个标准差)
• 超出界限则可能意味着生产线出现问题

---

四、常见误区

1. ​误区一​：认为原始数据必须正态分布

   • 实际上，CLT告诉我们无论原始分布如何，样本均值的分布都趋近正态

2. ​误区二​：忽视样本量的重要性

   • 对于高度非正态的分布(如指数分布)，可能需要更大的n才能良好近似

3. ​误区三​：混淆样本分布和抽样分布

   • 样本分布是原始数据的分布
   • 抽样分布是统计量(如样本均值)的分布

---

五、实际应用建议

1. ​确定适当样本量​：根据数据特性，可能需要n>30或更大
2. ​检查近似效果​：对于小样本或极端分布，可通过模拟验证正态近似是否合理
3. ​注意独立性假设​：CLT要求样本是独立的，在时间序列或空间数据中需谨慎
4. ​结合其他方法​：对于小样本，考虑使用t分布或其他非参数方法

---

六、总结

中心极限定理之所以重要，是因为它让我们能够：

• 对未知分布的数据进行推断
• 构建置信区间和进行假设检验
• 简化复杂问题的分析
• 理解为什么正态分布在自然界中如此普遍

---

七、解释

1、“均值的标准化形式”详解

---

1. 标准化的本质：统一量纲

想象你在比较：北京房价（均价6万/㎡，标准差2万），纽约房价（均价80万美元，标准差30万），直接比较“6万”和“80万”毫无意义！标准化就是将它们转换为无单位的统一尺度，从而可比。

---

2. 均值标准化的数学定义

对于样本均值，其标准化形式为：

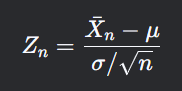
• 分子：均值与真实值的偏差（去中心化）

• 分母：均值的标准差（缩放至单位方差）

类比：假设全班考试平均分分，标准差。

• 当n=1时（单次观测），公式简化为Z=(X-μ)/σ

• 你的成绩

• 标准化值
  → 你比平均分高1.5个标准差（无论原始分数单位是分、美元还是厘米）

---

3. 几何直观：拉伸与平移

• 平移（分子）：把分布曲线的中心移到0

• 缩放（分母）：调整分布宽度，使标准差变为1

---

4. 记忆口诀

“减均值，除标准差，数据变身标准分”—— 就像把不同货币兑换成美元后再比较！

5. 练习

假设某App日活用户均值万人，标准差万。某天日活1.5万人，其标准化值是多少？
答案：（即“高出平均值1个标准差”）

2、“标准差为8cm”和“样本平均身高的标准差”​

想象你是一位老师，负责测量全班同学的身高。

​1. 单次测量的波动（原始标准差：标准差为8cm）​​

• 每个学生的身高都不一样，有的高，有的矮。
• ​原始标准差（σ）​​ 衡量的是“单个学生身高”的波动程度。比如，σ=8cm，意味着大部分学生的身高在“平均身高±8cm”之间。

​2. 多次测量平均值的波动（标准误差：样本平均身高的标准差）​​

现在，你不满足于只看单个学生的身高，而是想计算全班平均身高。

• 如果你只测5个学生，算出的平均身高可能和真实平均差很多（比如碰巧抽到了几个特别高的）。
• 如果你测50个学生，算出的平均身高会更接近真实值（因为极端值的影响被“平均”掉了）。

​样本平均身高的标准差（标准误差）​​ 衡量的是：

​​“不同样本的平均身高”之间的波动有多大？​​

计算公式：

​3. 为什么除以√n？​​

• ​样本量越大，平均值越稳定​（极端值的影响被稀释）。
• ​√n 的数学意义：
  • 如果样本量从 4 增加到 16（4倍），标准误差会减半（因为 √16=4，σ/4 比 σ/2 更小）。
  • 这就是为什么“大样本调查更可靠”！

​4. 现实例子​

假设：

• 全国10岁儿童身高的原始标准差 σ=8cm。
• 你调查了 ​100个孩子​（n=100），计算平均身高。

那么：

这意味着：

• 如果你重复抽样100人很多次，​不同样本的平均身高​ 会在“真实平均±0.8cm”之间波动。
• 对比单次测量的波动（±8cm），平均值的波动（±0.8cm）小得多！

​5. 类比：咖啡店排队时间​

• ​单次排队时间​：有时5分钟，有时30分钟（波动大，σ=10分钟）。
• ​平均10次排队的等待时间​：波动会小很多（σ/√10 ≈ 3.16分钟）。
• ​平均100次排队的等待时间​：波动更小（σ/√100 = 1分钟）。

​结论​：

• ​标准误差​ 告诉你，​样本均值有多可靠。
• ​样本量越大，均值越精准​（就像多次测量取平均会更准一样）。

扩大样本量可以减少误差。