《算法导论》第 16 章

大家好！今天我们来深入探讨《算法导论》第 16 章的核心内容 —— 贪心算法。贪心算法是一种在每一步选择中都采取在当前状态下最好或最优（即最有利）的选择，从而希望导致结果是全局最好或最优的算法。它在许多优化问题中都有广泛应用，如活动安排、哈夫曼编码、最小生成树等。

接下来，我们将按照教材的结构，逐一讲解各个知识点，并提供完整的 C++ 代码实现，帮助大家更好地理解和应用贪心算法。

16.1 活动选择问题

活动选择问题是贪心算法的经典应用案例，问题描述如下：

问题： 假设有 n 个活动，这些活动共享同一个资源（如会议室），而这个资源在同一时间只能供一个活动使用。每个活动 i 都有一个开始时间 s [i] 和结束时间 f [i]，其中 0 ≤ s [i] < f [i] < ∞。如果两个活动的时间区间不重叠，则它们是兼容的。活动选择问题就是要选择出一个最大的兼容活动集。

贪心策略分析

对于活动选择问题，有多种可能的贪心策略：

选择最早开始的活动
选择最短持续时间的活动
选择最晚开始的活动
选择最早结束的活动

经过分析，选择最早结束的活动这一策略能够得到最优解。其核心思想是：尽早结束当前活动，以便为后续活动留出更多时间。

代码实现

下面是活动选择问题的 C++ 实现，包括递归版本和迭代版本：

#include <iostream>
#include <vector>
#include <algorithm>using namespace std;// 活动结构体：开始时间、结束时间、活动编号
struct Activity {int start;int finish;int index;
};// 按结束时间升序排序的比较函数
bool compareFinish(const Activity& a, const Activity& b) {return a.finish < b.finish;
}/*** 迭代版本的活动选择算法* @param activities 活动列表* @return 选中的活动索引列表*/
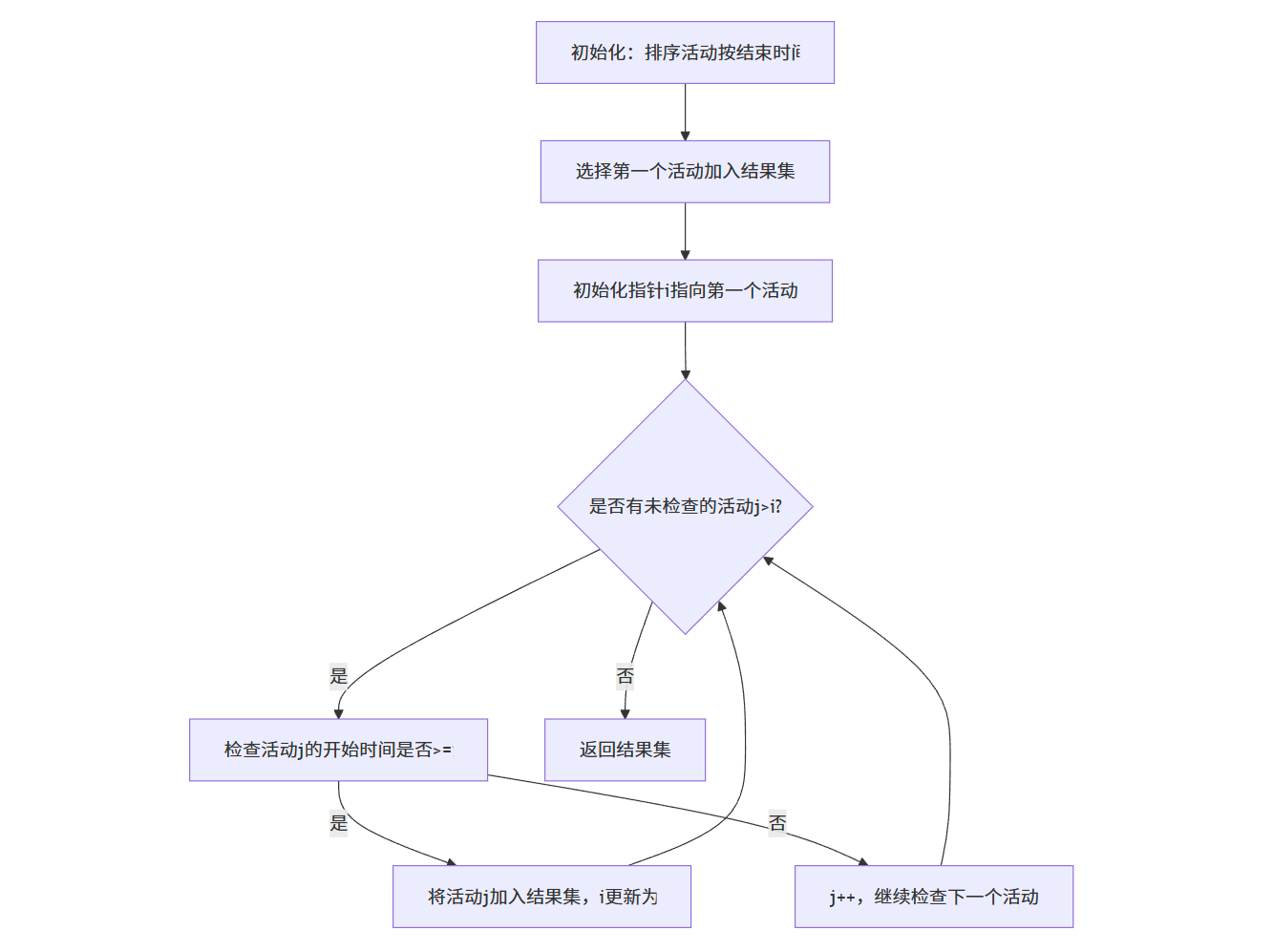
vector<int> selectActivitiesIterative(vector<Activity>& activities) {// 按结束时间排序sort(activities.begin(), activities.end(), compareFinish);vector<int> selected;int n = activities.size();// 选择第一个活动selected.push_back(activities[0].index);int lastSelected = 0;// 依次检查后续活动for (int i = 1; i < n; i++) {// 如果当前活动的开始时间 >= 最后选中活动的结束时间，则选择该活动if (activities[i].start >= activities[lastSelected].finish) {selected.push_back(activities[i].index);lastSelected = i;}}return selected;
}/*** 递归版本的活动选择算法* @param activities 活动列表（已排序）* @param index 当前检查的索引* @param n 活动总数* @param selected 已选中的活动索引列表*/
void selectActivitiesRecursive(const vector<Activity>& activities, int index, int n, vector<int>& selected) {// 找到第一个与最后选中活动兼容的活动int i;for (i = index; i < n; i++) {if (i == 0 || activities[i].start >= activities[selected.back()].finish) {break;}}if (i < n) {// 选择该活动selected.push_back(activities[i].index);// 递归选择剩余活动selectActivitiesRecursive(activities, i + 1, n, selected);}
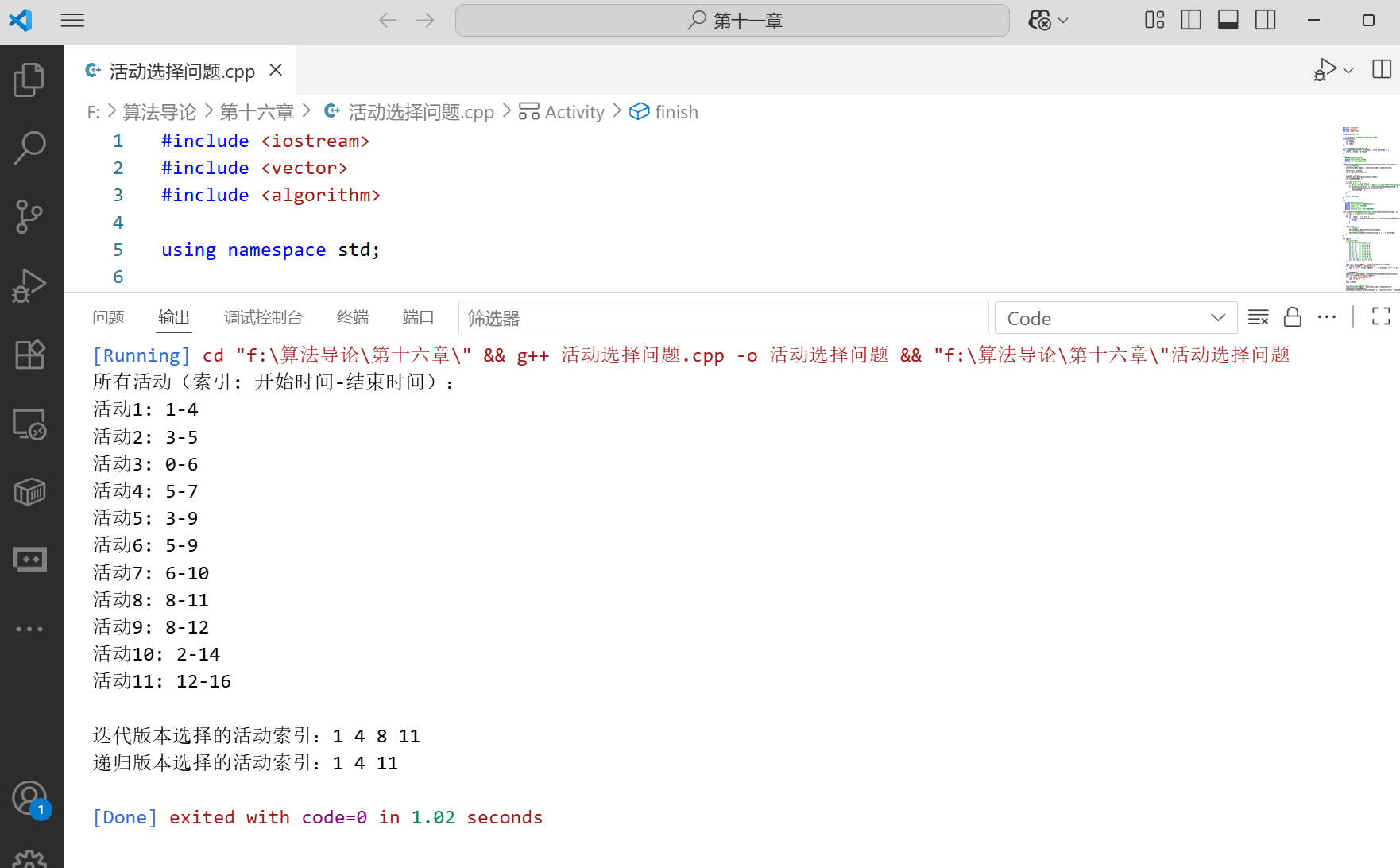
}int main() {// 示例活动数据vector<Activity> activities = {{1, 4, 1},   // 活动1: 1-4{3, 5, 2},   // 活动2: 3-5{0, 6, 3},   // 活动3: 0-6{5, 7, 4},   // 活动4: 5-7{3, 9, 5},   // 活动5: 3-9{5, 9, 6},   // 活动6: 5-9{6, 10, 7},  // 活动7: 6-10{8, 11, 8},  // 活动8: 8-11{8, 12, 9},  // 活动9: 8-12{2, 14, 10}, // 活动10: 2-14{12, 16, 11} // 活动11: 12-16};cout << "所有活动（索引: 开始时间-结束时间）：" << endl;for (const auto& act : activities) {cout << "活动" << act.index << ": " << act.start << "-" << act.finish << endl;}// 测试迭代版本vector<int> selectedIter = selectActivitiesIterative(activities);cout << "\n迭代版本选择的活动索引：";for (int idx : selectedIter) {cout << idx << " ";}cout << endl;// 测试递归版本（需要先排序）sort(activities.begin(), activities.end(), compareFinish);vector<int> selectedRecur;selectActivitiesRecursive(activities, 0, activities.size(), selectedRecur);cout << "递归版本选择的活动索引：";for (int idx : selectedRecur) {cout << idx << " ";}cout << endl;return 0;
}

代码说明

首先定义了Activity结构体来存储活动的开始时间、结束时间和索引
实现了按结束时间排序的比较函数compareFinish
迭代版本算法：
- 先对活动按结束时间排序
- 选择第一个活动，然后依次选择与最后选中活动兼容的活动
递归版本算法：
- 在已排序的活动列表中，找到第一个与最后选中活动兼容的活动
- 递归处理剩余活动
主函数中提供了示例数据，并测试了两种版本的算法

运行上述代码，会输出选中的活动索引，两种方法得到的结果是一致的。这验证了贪心算法在活动选择问题上的有效性。

16.2 贪心算法原理

贪心算法通过一系列选择来构造问题的解。在每一步，它选择在当前看来最好的选项，而不考虑过去的选择，也不担心未来的后果。这种 "短视" 的选择策略在某些问题上能够得到最优解。

贪心算法的核心要素

要使用贪心算法解决问题，通常需要满足以下两个关键性质：

贪心选择性质：全局最优解可以通过一系列局部最优选择（即贪心选择）来得到。也就是说，在做出选择时，我们只需要考虑当前状态下的最优选择，而不需要考虑子问题的解。
最优子结构性质：问题的最优解包含其子问题的最优解。如果我们做出了一个贪心选择，那么剩下的问题可以转化为一个更小的子问题，而这个子问题的最优解可以与我们的贪心选择结合，形成原问题的最优解。

贪心算法与动态规划的对比

贪心算法和动态规划都用于解决具有最优子结构的问题，但它们的策略不同：

特性	贪心算法	动态规划
决策方式	每次选择局部最优，不回溯	自底向上或自顶向下计算，保存子问题解
适用问题	具有贪心选择性质的问题	所有具有最优子结构的问题
时间复杂度	通常较低（O (n log n) 或 O (n)）	较高（通常为多项式时间）
例子	活动选择、哈夫曼编码	最长公共子序列、背包问题

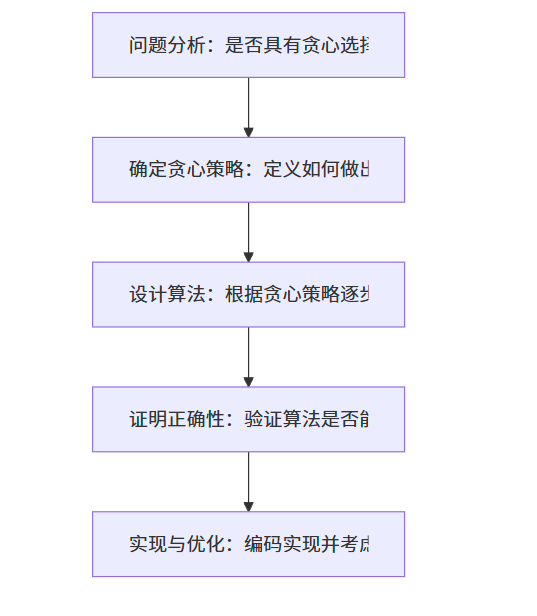
综合案例：找零问题

问题描述：假设货币系统有面额为 25、10、5、1 的硬币，如何用最少的硬币数找给顾客一定金额的零钱？

贪心策略：每次选择不超过剩余金额的最大面额硬币，直到找零完成。

#include <iostream>
#include <vector>
#include <algorithm>using namespace std;/*** 贪心算法解决找零问题* @param denominations 硬币面额（从大到小排序）* @param amount 需要找零的金额* @return 每种硬币的使用数量*/
vector<int> makeChange(const vector<int>& denominations, int amount) {vector<int> counts(denominations.size(), 0);int remaining = amount;for (int i = 0; i < denominations.size() && remaining > 0; i++) {// 选择当前最大面额的硬币counts[i] = remaining / denominations[i];// 更新剩余金额remaining -= counts[i] * denominations[i];}// 如果还有剩余金额，说明无法用给定面额找零if (remaining > 0) {return {}; // 返回空向量表示无法找零}return counts;
}int main() {// 硬币面额（从大到小排序）vector<int> denominations = {25, 10, 5, 1};int amount;cout << "请输入需要找零的金额：";cin >> amount;vector<int> counts = makeChange(denominations, amount);if (counts.empty()) {cout << "无法用给定的硬币面额完成找零" << endl;} else {cout << "找零 " << amount << " 需要的硬币数量：" << endl;int total = 0;for (int i = 0; i < denominations.size(); i++) {if (counts[i] > 0) {cout << denominations[i] << "分：" << counts[i] << "枚" << endl;total += counts[i];}}cout << "总共需要：" << total << "枚硬币" << endl;}return 0;
}

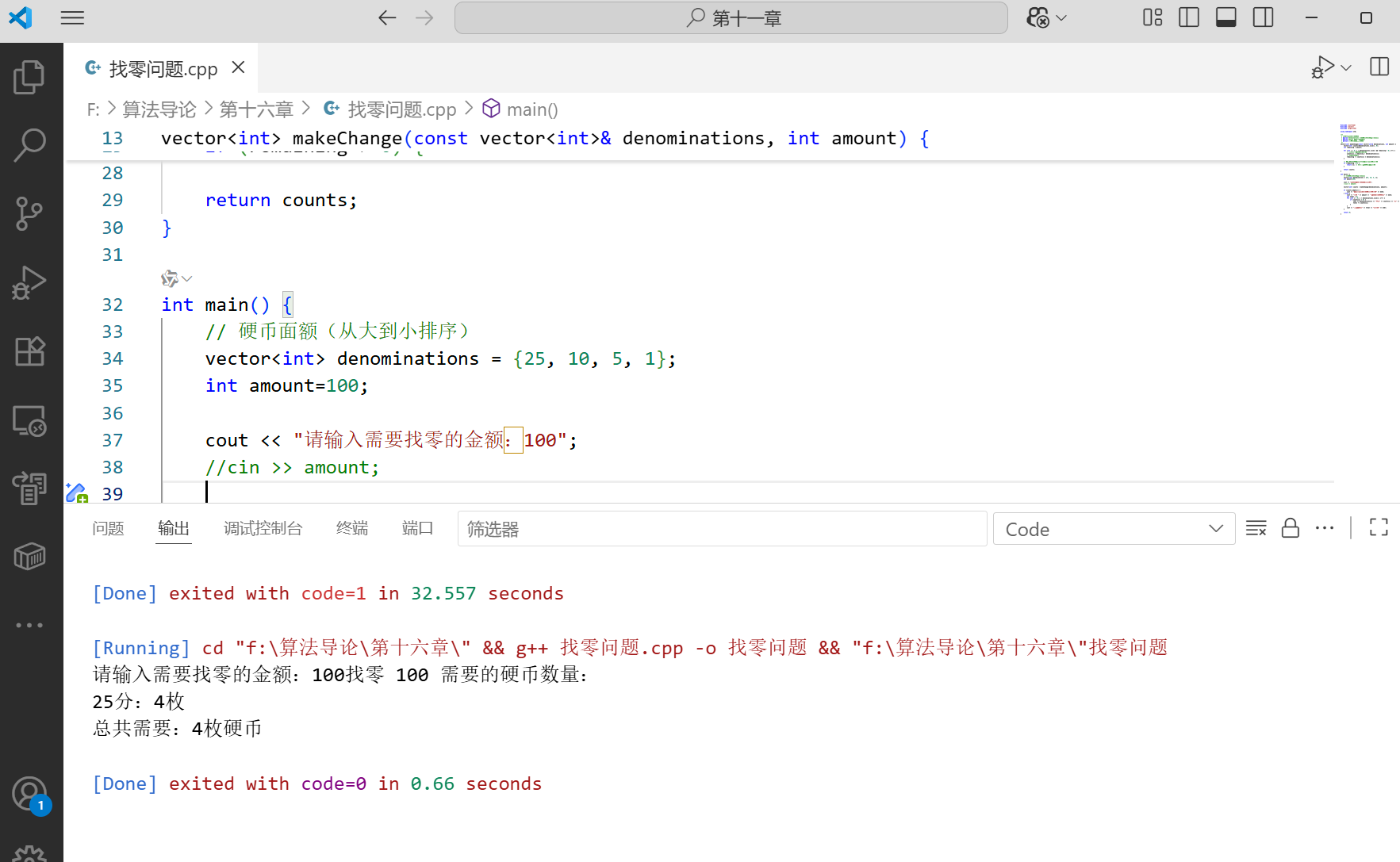
代码说明：

算法先对硬币面额从大到小排序（示例中已预先排序）
对于每种面额，计算最多能使用多少枚而不超过剩余金额
更新剩余金额，继续处理下一面额
如果最终剩余金额为 0，则返回各面额的使用数量；否则表示无法找零

注意：贪心算法并非在所有货币系统中都能得到最优解。例如，如果货币面额为 25、10、1，要找 30 元，贪心算法会选择 25+1+1+1+1+1（6 枚），但最优解是 10+10+10（3 枚）。因此，贪心算法的适用性取决于问题本身的特性。

16.3 赫夫曼编码

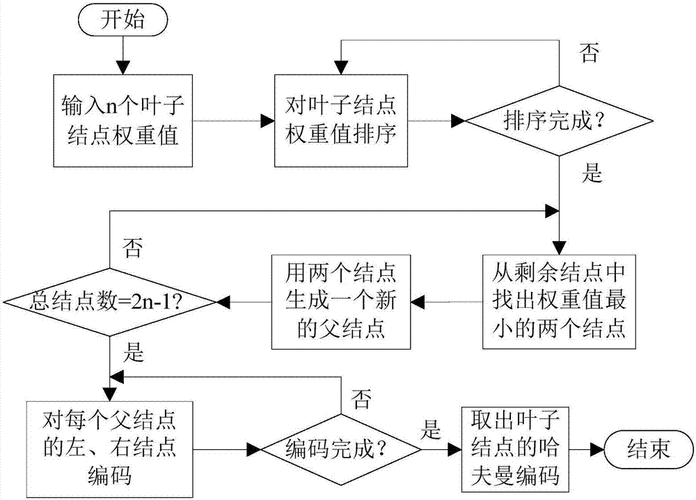
赫夫曼编码（Huffman Coding）是一种用于数据压缩的贪心算法，由 David A. Huffman 于 1952 年提出。它通过为出现频率较高的字符分配较短的编码，为出现频率较低的字符分配较长的编码，从而实现数据的高效压缩。

赫夫曼编码的基本概念

前缀码：一种编码方式，其中任何一个字符的编码都不是另一个字符编码的前缀。这种特性使得我们可以无需分隔符就能解码。
二叉树表示：赫夫曼编码通常用二叉树表示，左分支表示 0，右分支表示 1，树叶表示字符。
构建过程：基于字符出现的频率构建赫夫曼树，频率高的字符离根节点近（编码短），频率低的字符离根节点远（编码长）。

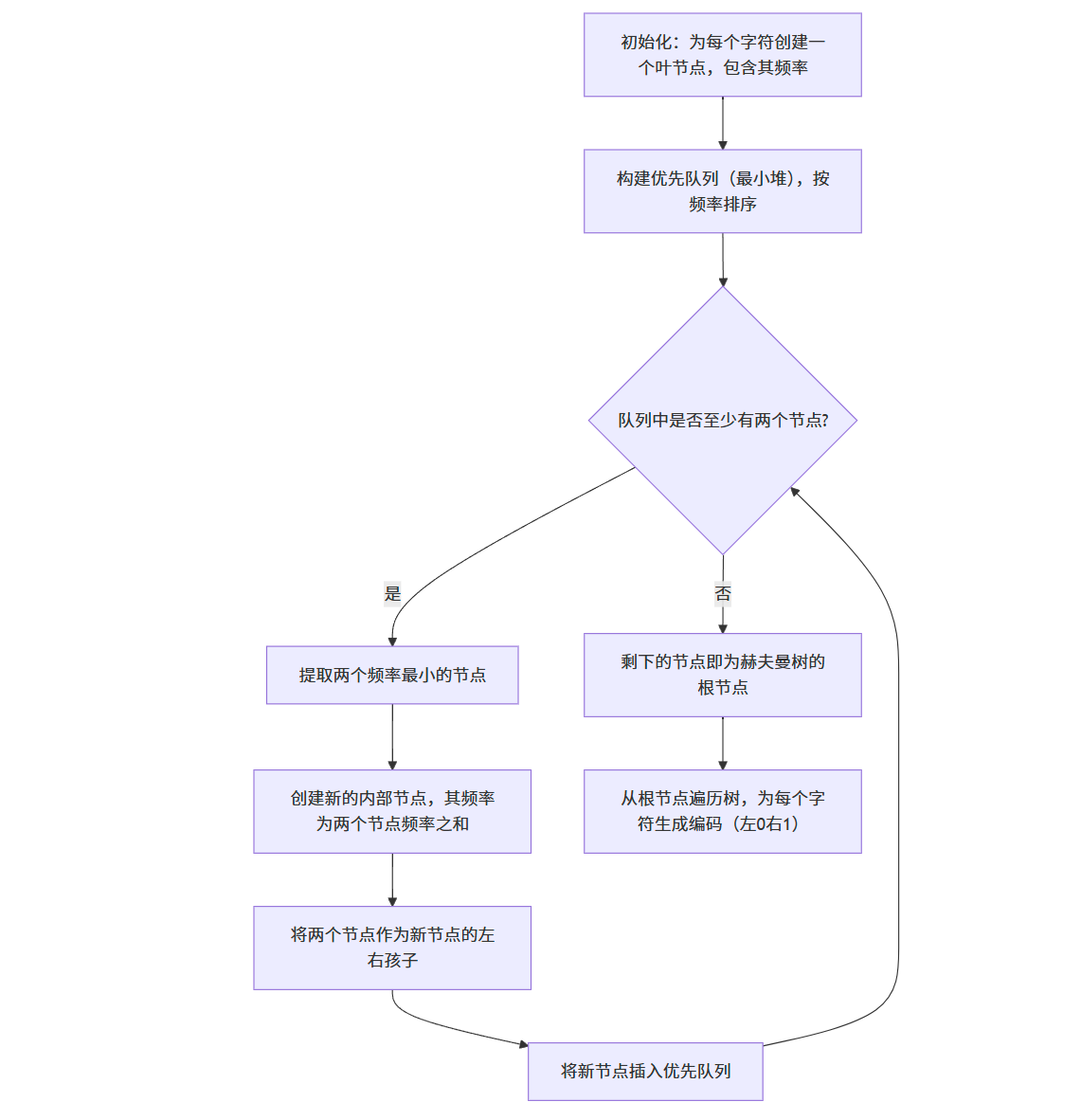
代码实现

下面是赫夫曼编码的完整 C++ 实现：

#include <iostream>
#include <vector>
#include <queue>
#include <unordered_map>
#include <string>
#include <memory>using namespace std;// 赫夫曼树节点
struct HuffmanNode {char data;           // 字符int freq;            // 频率shared_ptr<HuffmanNode> left, right; // 左右孩子HuffmanNode(char data, int freq) : data(data), freq(freq), left(nullptr), right(nullptr) {}
};// 优先队列的比较函数（最小堆）
struct CompareNodes {bool operator()(const shared_ptr<HuffmanNode>& a, const shared_ptr<HuffmanNode>& b) {return a->freq > b->freq; // 频率小的节点优先级高}
};/*** 构建赫夫曼树* @param freq 字符频率映射* @return 赫夫曼树的根节点*/
shared_ptr<HuffmanNode> buildHuffmanTree(const unordered_map<char, int>& freq) {// 创建优先队列（最小堆）priority_queue<shared_ptr<HuffmanNode>, vector<shared_ptr<HuffmanNode>>, CompareNodes> pq;// 为每个字符创建叶节点并加入队列for (const auto& pair : freq) {pq.push(make_shared<HuffmanNode>(pair.first, pair.second));}// 构建赫夫曼树while (pq.size() > 1) {// 提取两个频率最小的节点auto left = pq.top();pq.pop();auto right = pq.top();pq.pop();// 创建新的内部节点auto internal = make_shared<HuffmanNode>('$', left->freq + right->freq);internal->left = left;internal->right = right;// 将新节点加入队列pq.push(internal);}// 剩下的节点是根节点return pq.top();
}/*** 递归生成赫夫曼编码* @param root 赫夫曼树的根节点* @param currentCode 当前编码* @param huffmanCodes 存储生成的编码*/
void generateCodes(const shared_ptr<HuffmanNode>& root, string currentCode, unordered_map<char, string>& huffmanCodes) {if (!root) return;// 如果是叶节点，保存编码if (root->data != '$') {huffmanCodes[root->data] = currentCode.empty() ? "0" : currentCode;return;}// 递归处理左右子树generateCodes(root->left, currentCode + "0", huffmanCodes);generateCodes(root->right, currentCode + "1", huffmanCodes);
}/*** 编码字符串* @param str 原始字符串* @param huffmanCodes 赫夫曼编码映射* @return 编码后的二进制字符串*/
string encodeString(const string& str, const unordered_map<char, string>& huffmanCodes) {string encoded;for (char c : str) {encoded += huffmanCodes.at(c);}return encoded;
}/*** 解码二进制字符串* @param encoded 编码后的二进制字符串* @param root 赫夫曼树的根节点* @return 解码后的原始字符串*/
string decodeString(const string& encoded, const shared_ptr<HuffmanNode>& root) {string decoded;auto current = root;for (char bit : encoded) {if (bit == '0') {current = current->left;} else {current = current->right;}// 如果到达叶节点，添加字符并重置当前节点if (!current->left && !current->right) {decoded += current->data;current = root;}}return decoded;
}/*** 计算字符频率* @param str 输入字符串* @return 字符频率映射*/
unordered_map<char, int> calculateFrequency(const string& str) {unordered_map<char, int> freq;for (char c : str) {freq[c]++;}return freq;
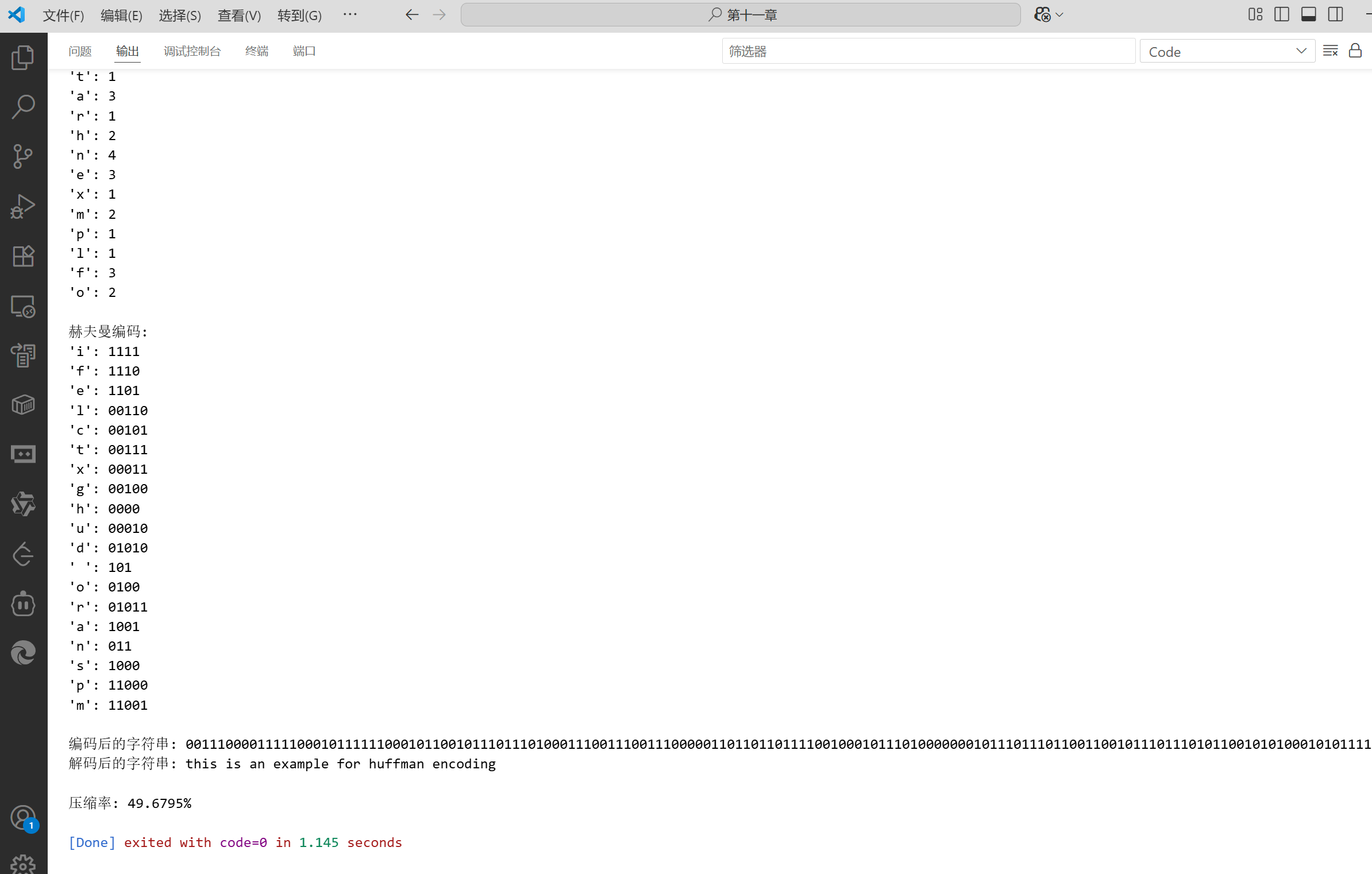
}int main() {string str = "this is an example for huffman encoding";cout << "原始字符串: " << str << endl;// 计算字符频率auto freq = calculateFrequency(str);cout << "\n字符频率:" << endl;for (const auto& pair : freq) {cout << "'" << pair.first << "': " << pair.second << endl;}// 构建赫夫曼树auto root = buildHuffmanTree(freq);// 生成赫夫曼编码unordered_map<char, string> huffmanCodes;generateCodes(root, "", huffmanCodes);cout << "\n赫夫曼编码:" << endl;for (const auto& pair : huffmanCodes) {cout << "'" << pair.first << "': " << pair.second << endl;}// 编码字符串string encoded = encodeString(str, huffmanCodes);cout << "\n编码后的字符串: " << encoded << endl;// 解码字符串string decoded = decodeString(encoded, root);cout << "解码后的字符串: " << decoded << endl;// 计算压缩率double originalSize = str.size() * 8; // 假设每个字符8位double compressedSize = encoded.size();double compressionRatio = 100 - (compressedSize / originalSize * 100);cout << "\n压缩率: " << compressionRatio << "%" << endl;return 0;
}

代码说明

HuffmanNode 结构体：表示赫夫曼树的节点，包含字符、频率和左右孩子指针
构建赫夫曼树：
- 使用优先队列（最小堆）存储节点
- 反复提取两个频率最小的节点，创建新的内部节点，直到只剩下一个节点（根节点）
生成编码：通过递归遍历赫夫曼树，为每个字符生成二进制编码（左 0 右 1）
编码与解码：
- 编码：将原始字符串转换为二进制编码字符串
- 解码：将二进制编码字符串还原为原始字符串
辅助功能：计算字符频率、计算压缩率等

运行上述代码，可以看到赫夫曼编码如何为频率高的字符分配较短的编码，从而实现数据压缩。

16.4 拟阵和贪心算法

拟阵（Matroid）是一种组合结构，它为我们提供了一个理解贪心算法有效性的通用框架。许多可以用贪心算法解决的问题都可以建模为拟阵上的优化问题。

代码实现（基于拟阵的活动选择）

我们可以用拟阵理论来重新实现活动选择问题，展示拟阵与贪心算法的关系：

#include <iostream>
#include <vector>
#include <algorithm>
#include <unordered_set>using namespace std;// 活动结构体
struct Activity {int start;int finish;int index;int weight; // 活动权重，用于加权活动选择问题
};// 按权重降序排序
bool compareWeight(const Activity& a, const Activity& b) {return a.weight > b.weight;
}// 检查活动集是否独立（即是否存在冲突）
bool isIndependent(const vector<Activity>& activities, const unordered_set<int>& selectedIndices) {vector<Activity> selected;for (int idx : selectedIndices) {selected.push_back(activities[idx]);}// 检查所有选中的活动是否两两不冲突for (int i = 0; i < selected.size(); i++) {for (int j = i + 1; j < selected.size(); j++) {// 如果两个活动时间重叠，则不独立if (!(selected[i].finish <= selected[j].start || selected[j].finish <= selected[i].start)) {return false;}}}return true;
}/*** 基于拟阵的贪心算法解决加权活动选择问题* @param activities 活动列表* @return 选中的活动索引集合*/
unordered_set<int> maxWeightIndependentSet(vector<Activity>& activities) {// 按权重降序排序sort(activities.begin(), activities.end(), compareWeight);unordered_set<int> selected;// 依次考虑每个活动for (int i = 0; i < activities.size(); i++) {// 尝试加入当前活动selected.insert(i);// 检查是否保持独立性if (!isIndependent(activities, selected)) {// 如果不独立，移除该活动selected.erase(i);}}return selected;
}int main() {// 带权重的示例活动数据vector<Activity> activities = {{1, 4, 1, 3},   // 活动1: 1-4, 权重3{3, 5, 2, 2},   // 活动2: 3-5, 权重2{0, 6, 3, 4},   // 活动3: 0-6, 权重4{5, 7, 4, 5},   // 活动4: 5-7, 权重5{3, 9, 5, 1},   // 活动5: 3-9, 权重1{5, 9, 6, 6},   // 活动6: 5-9, 权重6{6, 10, 7, 7},  // 活动7: 6-10, 权重7{8, 11, 8, 8},  // 活动8: 8-11, 权重8{8, 12, 9, 9},  // 活动9: 8-12, 权重9{2, 14, 10, 10}, // 活动10: 2-14, 权重10{12, 16, 11, 11} // 活动11: 12-16, 权重11};// 应用基于拟阵的贪心算法auto selected = maxWeightIndependentSet(activities);// 计算总权重int totalWeight = 0;for (int idx : selected) {totalWeight += activities[idx].weight;}cout << "选中的活动（索引）：";for (int idx : selected) {cout << activities[idx].index << " ";}cout << endl;cout << "选中的活动详情：" << endl;for (int idx : selected) {const auto& act = activities[idx];cout << "活动" << act.index << ": " << act.start << "-" << act.finish << ", 权重: " << act.weight << endl;}cout << "总权重：" << totalWeight << endl;return 0;
}

代码说明

这个例子实现了加权活动选择问题，与 16.1 节的问题不同，这里每个活动都有一个权重，我们的目标是选择总权重最大的兼容活动集。
我们将这个问题建模为拟阵问题：
- 集合 S 是所有活动的集合
- 独立集 \(\mathcal{I}\) 是所有不冲突的活动子集（即任意两个活动时间不重叠）
算法步骤：
- 将活动按权重降序排序
- 依次考虑每个活动，如果加入后仍保持独立性（即与已选活动不冲突），则选中该活动
- 最终得到的集合是总权重最大的独立集
isIndependent函数用于检查一个活动集合是否是独立集（即不包含冲突的活动）

这个例子展示了拟阵理论如何为贪心算法提供理论基础，以及如何将实际问题建模为拟阵上的优化问题。

16.5 用拟阵求解任务调度问题

任务调度是计算机科学中的一个重要问题，我们可以利用拟阵理论和贪心算法来求解某些类型的任务调度问题。

问题描述

考虑一个单处理器的任务调度问题：

代码实现

#include <iostream>
#include <vector>
#include <algorithm>
#include <unordered_set>using namespace std;// 任务结构体
struct Task {int id;         // 任务IDint t;          // 处理时间int w;          // 权重int d;          // 截止时间
};// 按权重/处理时间比值降序排序
bool compareRatio(const Task& a, const Task& b) {// 避免浮点数运算，使用交叉相乘比较return (long long)a.w * b.t > (long long)b.w * a.t;
}// 按截止时间升序排序
bool compareDeadline(const Task& a, const Task& b) {return a.d < b.d;
}/*** 检查任务集是否可以被可行调度* @param tasks 要检查的任务集* @return 如果可以被可行调度，返回true；否则返回false*/
bool isFeasible(vector<Task> tasks) {// 按截止时间升序排序sort(tasks.begin(), tasks.end(), compareDeadline);int totalTime = 0;for (const auto& task : tasks) {totalTime += task.t;// 检查前缀和是否超过当前任务的截止时间if (totalTime > task.d) {return false;}}return true;
}/*** 用拟阵和贪心算法求解任务调度问题* @param tasks 所有任务的列表* @return 选中的任务集合*/
vector<Task> scheduleTasks(vector<Task>& tasks) {// 按权重/处理时间比值降序排序sort(tasks.begin(), tasks.end(), compareRatio);vector<Task> selected;// 依次考虑每个任务for (const auto& task : tasks) {// 尝试加入当前任务selected.push_back(task);// 检查是否仍能可行调度if (!isFeasible(selected)) {// 如果不可行，移除该任务selected.pop_back();}}return selected;
}int main() {// 示例任务数据vector<Task> tasks = {{1, 3, 10, 6},   // 任务1: t=3, w=10, d=6{2, 2, 20, 4},   // 任务2: t=2, w=20, d=4{3, 1, 5, 3},    // 任务3: t=1, w=5, d=3{4, 4, 40, 10},  // 任务4: t=4, w=40, d=10{5, 2, 15, 5},   // 任务5: t=2, w=15, d=5{6, 5, 25, 15}   // 任务6: t=5, w=25, d=15};// 应用调度算法vector<Task> scheduled = scheduleTasks(tasks);// 计算总权重int totalWeight = 0;for (const auto& task : scheduled) {totalWeight += task.w;}// 按截止时间排序以显示调度顺序sort(scheduled.begin(), scheduled.end(), compareDeadline);cout << "选中的任务（按调度顺序）：" << endl;int currentTime = 0;for (const auto& task : scheduled) {cout << "任务" << task.id << ": 开始时间=" << currentTime << ", 结束时间=" << currentTime + task.t << ", 截止时间=" << task.d << ", 权重=" << task.w << endl;currentTime += task.t;}cout << "总权重：" << totalWeight << endl;return 0;
}

代码说明

这个实现解决了带截止时间和权重的单处理器任务调度问题，目标是最大化总权重同时满足所有截止时间约束。
算法核心步骤：
- 按权重 / 处理时间比值降序排序任务（优先考虑 "单位时间价值" 高的任务）
- 依次尝试添加任务，每次添加后检查是否仍能找到可行的调度方案
- 可行调度检查：按截止时间排序任务，确保所有前缀和（累计处理时间）不超过对应任务的截止时间
最终输出的是按截止时间排序的任务，这代表了一种可行的调度顺序。

这个例子展示了如何将实际问题建模为拟阵问题，并应用贪心算法求解，体现了拟阵理论在贪心算法中的基础作用。

思考题

活动选择问题中，如果活动有不同的权重，我们希望选择总权重最大的兼容活动集，此时 16.1 节的贪心算法是否仍然适用？为什么？
证明赫夫曼编码产生的是最优前缀码。
考虑 0-1 背包问题：有 n 个物品，每个物品有重量 w_i 和价值 v_i，背包容量为 W，如何选择物品使得总价值最大且总重量不超过 W。为什么贪心算法（如按价值 / 重量比排序）不能保证得到最优解？这个问题是否可以建模为拟阵问题？
设计一个基于贪心算法的算法，用于求解区间图的最小顶点覆盖问题。
考虑一个有向图的最短路径问题，从源点到其他所有顶点的最短路径。Dijkstra 算法是一种贪心算法，它的贪心策略是什么？为什么在存在负权边的情况下 Dijkstra 算法可能失效？