一、酶作用优化算法

酶作用优化（Enzyme Action Optimizer, EAO）算法是一种2025年提出的新型仿生优化算法，灵感源于生物系统中酶的催化机制，发表于JCR 2区期刊《The Journal of Supercomputing》。其核心思想是模拟酶与底物的特异性结合、催化反应及动态适应过程，通过平衡搜索空间的探索与开发，实现复杂优化问题的高效求解。

1. 核心机制与数学建模

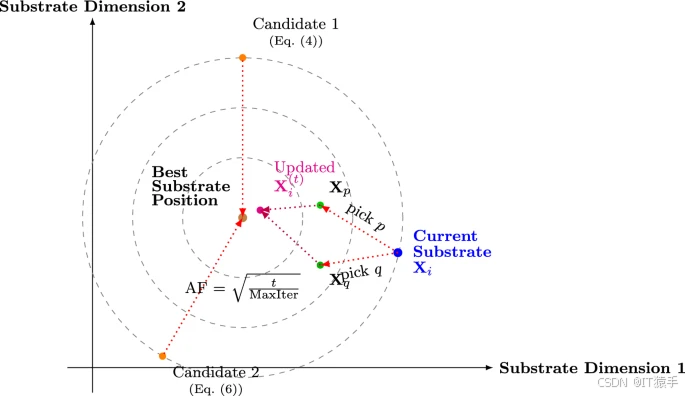
• 初始化：搜索代理（模拟“底物”）在解空间内随机初始化，位置满足：
  $${\mathbf{X}}_i^{(0)}=\text{LB}+(\text{UB}-\text{LB})\odot {\mathbf{r}}_i$$
  其中$\text{LB}$和$\text{UB}$为变量上下界，${\mathbf{r}}_i$为$(0,1)$区间随机向量，$\odot$表示元素乘法。初始适应度通过目标函数$f({\mathbf{X}}_i^{(0)})$评估，最优初始位置记为${\mathbf{X}}_{\text{best}}^{(0)}$。

• 自适应因子（AF）：随迭代动态调整，平衡探索与开发：
  $${\text{AF}}_t=\sqrt{\frac{t}{\text{MaxIter}}}$$
  其中$t$为当前迭代，$\text{MaxIter}$为最大迭代次数，确保后期逐步聚焦局部搜索。

• 候选位置生成：每次迭代中，每个底物生成两个候选位置：

  1. 基于当前最优解（模拟“酶”）的定向搜索：
     $${\mathbf{X}}_{i,1}^{(t)}=({\mathbf{X}}_{\text{best}}^{(t-1)}-{\mathbf{X}}_i^{(t-1)})+{\rho }_i\odot \sin ({\text{AF}}_t\cdot ({\mathbf{X}}_{\text{best}}^{(t-1)}-{\mathbf{X}}_i^{(t-1)}))$$
     其中${\rho }_i$为随机向量，正弦函数引入波动以增强探索。
  2. 基于随机底物差异的多样化搜索：
     $${\mathbf{X}}_{i,2}^{(t)}={\mathbf{X}}_i^{(t-1)}+s{c}_1\mathbf{d}+{\text{AF}}_t\cdot s{c}_2({\mathbf{X}}_{\text{best}}^{(t-1)}-{\mathbf{X}}_i^{(t-1)})$$
     其中$\mathbf{d}$为两个随机底物的位置差，$s{c}_1,s{c}_2$为缩放因子（受酶浓度参数$\text{EC}$调控）。

• 更新策略：选择适应度更优的候选位置更新底物，同时更新全局最优解${\mathbf{X}}_{\text{best}}$，确保解始终在可行域内。
  

2. 算法特点

EAO通过模拟酶的自适应催化特性，动态平衡广域探索（随机扰动）与局部开发（定向收敛），在多维复杂优化问题中表现出良好的收敛速度与鲁棒性。其核心优势在于利用酶-底物相互作用的特异性，实现对优质解区域的精准挖掘。

参考文献
[1]Rodan, A., Al-Tamimi, AK., Al-Alnemer, L. et al. Enzyme action optimizer: a novel bio-inspired optimization algorithm. J Supercomput 81, 686 (2025). https://doi.org/10.1007/s11227-025-07052-w.

二、多目标酶作用优化算法

针对单目标优化问题，酶作用优化算法已显示出其有效性。然而，在面对多目标优化问题时，需要一种能够同时处理多个冲突目标的算法。因此，本文提出多目标加权平均算法（Multi-objective Enzyme Action Optimizer, MOEAO）。

为了评估MOEAO的性能，我们将其应用于一组标准的基准测试函数，这组函数包括MaF1-MaF15及工程应用—盘式制动器设计。这些函数在测试多目标优化算法的效率方面被广泛采用。此外，为了全面评估算法的收敛性和解的多样性，我们使用了六种不同的性能度量指标：GD、IGD、HV、Spacing、Spread和Coverage。通过这些指标的综合分析，我们可以有效地评估该算法在处理多目标优化问题时的整体性能。
盘式制动器设计的数学模型如下：

MOEAO算法的执行步骤可以描述如下：

2.1、六种性能评价指标介绍

1. GD（Generational Distance）世代距离：
   GD指标用于评价获得的帕累托前沿（PF）和最优帕累托前沿之间的距离。对于每个属于PF的解，找到与其最近的最优帕累托前沿中的解，计算其欧式距离，GD为这些最短欧式距离的平均值。GD值越小，代表收敛性越好，找到的PF与最优帕累托前沿越接近。

2. IGD（Inverted Generational Distance）逆世代距离：
   IGD与GD相似，但同时考虑了多样性和收敛性。对于真实的最优帕累托前沿中的每个解，找到与其最近的PF中的解，计算其欧式距离，取平均值而不需开方。如果PF的数量大于最优帕累托前沿的数量，那么IGD就能最完整地表达PF的性能，IGD值越小，代表算法多样性和收敛性越好。

3. HV（Hypervolume）超体积：
   HV也称为S metric，用于评价目标空间被一个近似集覆盖的程度，是最为普遍的一种评价指标。需要用到一个参考点，HV值为PF与参考点之间组成的超立方体的体积。HV的比较不需要先验知识，不需要找到真实的帕累托前沿。如果某个近似集A完全支配另一个近似集B，那么A的超容量HV会大于B，因此HV完全可以用于Pareto比较。

4. Spacing：
   Spacing是衡量算法生成的非支配解集中各个解之间平均距离的指标。Spacing值越小，表示解集内部的解越密集，多样性越高。

5. Spread：
   Spread指标衡量算法生成的非支配解集在Pareto前沿上的分散程度。高的Spread值意味着解集在前沿上分布得更均匀，没有聚集在某个区域。

6. Coverage：
   Coverage指标衡量一个算法生成的Pareto前沿覆盖另一个算法生成的Pareto前沿的比例。如果算法A的Coverage指标高于算法B，那么意味着算法A生成的Pareto前沿在某种程度上包含了算法B生成的Pareto前沿。

2.2、部分MATLAB代码

%% 参数说明
%testProblem 测试问题序号
%Name 测试问题名称
%dim 测试问题维度
%numObj测试问题目标函数个数
%lb测试问题下界
%ub测试问题上界
%SearchAgents_no 种群大小
%Max_iter最大迭代次数
%Fbest 算法求得的POF
%Xbest 算法求得的POS
%TurePF 测试问题的真实pareto前沿
%Result 评价指标
testProblem=2;
[Name,dim,numObj,lb,ub]=GetProblemInfo(testProblem);%获取测试问题的相关信息
SearchAgents_no=200;%种群大小 
Max_iter=200;%最大迭代次数
[Fbest,Xbest] = MOWAA(Max_iter,SearchAgents_no,Name,dim,numObj,lb,ub);%算法求解

2.3、部分结果

三、完整MATLAB代码见下方名片