- 1792C 逆向思维
- 1036D 前缀和+尺取
- 1598D 组合数学取三元组 将二元组放在坐标系中更好找到规律
1792C 思维 1500
参考题解
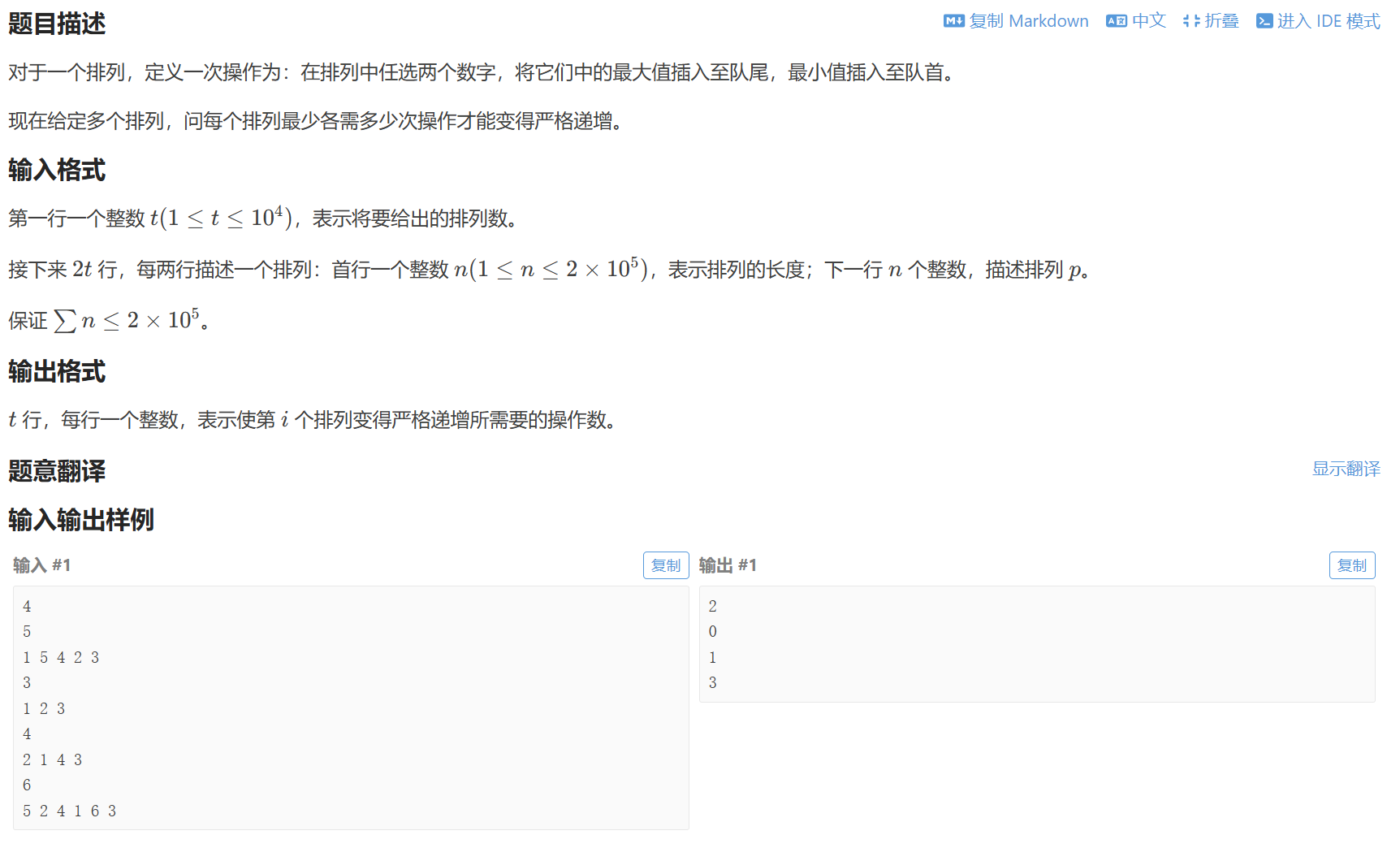
正难则反
注意是对一个排列进行操作,最后还原成1,2,…,n
每次选两个数字很难想,反着想就是把1-n的排列变成所给数组的逆操作,从外向内(1,n),(2,n−1),...(1,n),(2,n-1),...(1,n),(2,n−1),...一对一对还原
所以正着操作就是从内向外选(n/2,n/2+1),(n/2−1,n/2+2),...(n/2,n/2+1),(n/2-1,n/2+2),...(n/2,n/2+1),(n/2−1,n/2+2),...,顺序正确就不需要操作,一旦逆序,剩下的都要操作
void solve(){int n;cin>>n;vector<int>a(n+1),id(n+1);forr(i,1,n){cin>>a[i];id[a[i]]=i;}int ans=0;int mid=n/2;reforr(i,1,mid){if(id[i]<id[i+1]&&id[n-i+1]>id[n-i])continue;else{ans=i;break;}}cout<<ans<<endl;}
1036D 前缀和+尺取法 1600
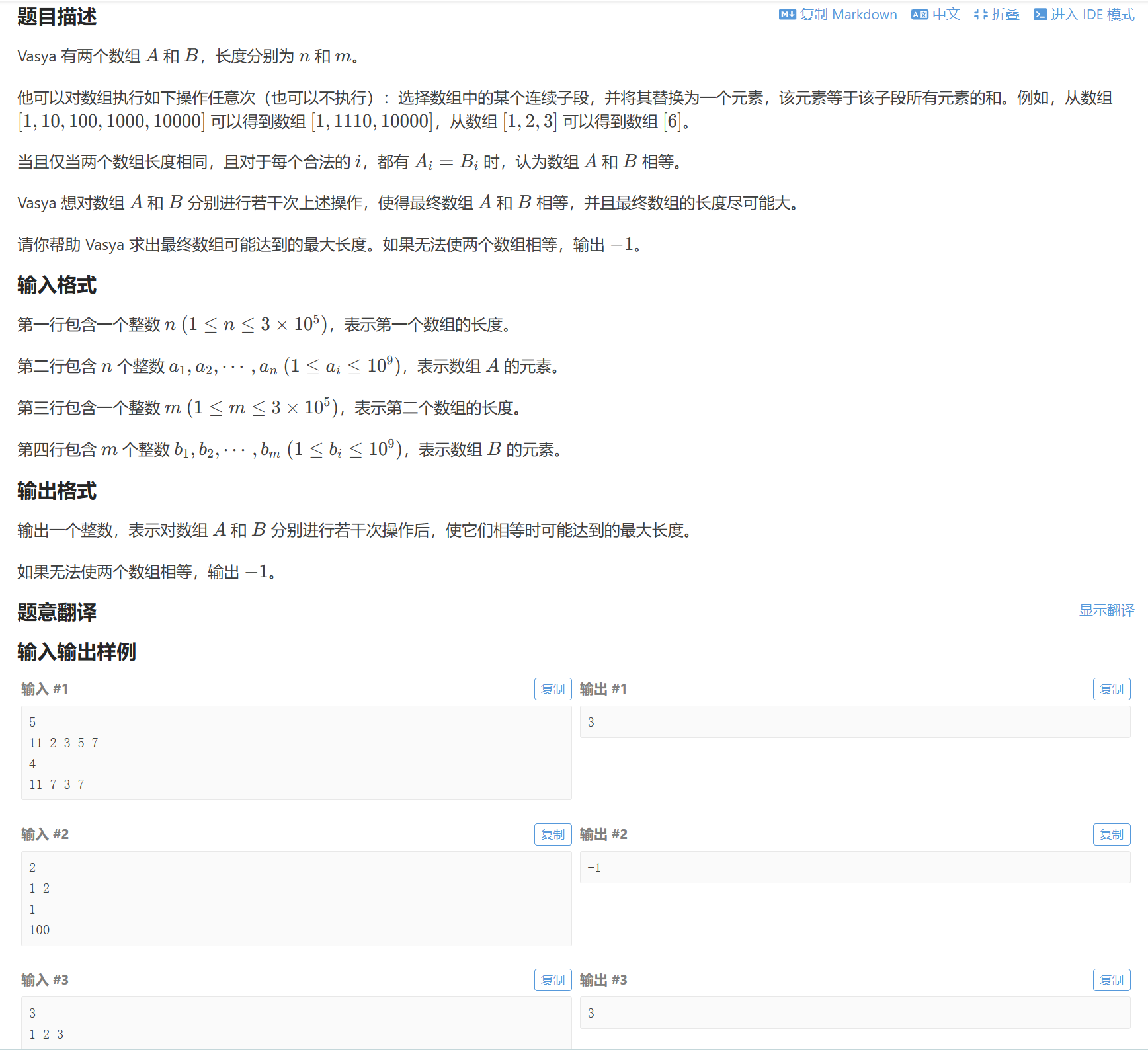
前缀和相等 说明其中的区间和相等 可以和上一个前缀和相等的地方对消
void solve(){int n,m;cin>>n;vector<int>a(n+1);forr(i,1,n){cin>>a[i];a[i]+=a[i-1];}cin>>m;vector<int>b(m+1);forr(i,1,m){cin>>b[i];b[i]+=b[i-1];}if(a[n]!=b[m])return cout<<-1<<endl,void();int ia=1,ib=1,ans=0;while (ia<=n&&ib<=m){if(a[ia]==b[ib])ans++,ia++,ib++;else if(a[ia]>b[ib])ib++;else if(a[ia]<b[ib])ia++;}cout<<(ans==0?-1:ans)<<endl;
}
1598D 组合数学 思维 1700

把(a,b)数对放在直角坐标系中
来自dalao的思路
再次转化不合法方案的条件:
- 三个点中有两个点横坐标一致;
- 三个点中有两个点纵坐标一致。
通俗一点说,这三个点在二维平面上组成了一个 L 形(当然,这个 L 形也有可能是旋转过的)。
那么,我们不妨枚举这个 L 形上拐弯处那个点,这样就可以求出不合法的方案数了。
void solve(){int n;cin>>n;vector<int>a(n+1),b(n+1);map<int,int>ma,mb;forr(i,1,n){cin>>a[i]>>b[i];ma[a[i]]++,mb[b[i]]++;}int ans=n*(n-1)*(n-2)/6;//总数forr(i,1,n){ans-=(ma[a[i]]-1)*(mb[b[i]]-1);//去掉重复的}cout<<ans<<endl;
}
)

)


、ReadKey()和ReadLine()))




和常见配置镜像加速)




![[系统架构设计师]系统质量属性与架构评估(八)](http://pic.xiahunao.cn/[系统架构设计师]系统质量属性与架构评估(八))
)


