前言
在时间序列预测领域,集成学习方法一直占据重要地位。此前我们介绍了基于传统集成思想的时序预测方法(查看前文),而梯度提升树(GBDT)作为集成学习的佼佼者,在时序预测中表现尤为突出。本文将重点讲解 LightGBM 算法的原理、优势及其在时序预测中的应用,并介绍如何使用粒子群优化(PSO)算法寻找最优参数,提升预测精度。
1: LightGBM 算法原理简介与应用
1.1 LightGBM 基本原理
LightGBM(Light Gradient Boosting Machine)是微软于 2017 年开源的梯度提升框架,基于决策树的集成学习算法,核心思想是通过不断迭代训练弱分类器(决策树) 来修正上一轮的预测误差,最终形成强分类器。
与传统 GBDT 相比,LightGBM 创新性地提出了两种关键技术:
- histogram-based 决策树学习 :将连续特征值离散化为直方图(bin),减少分裂时的计算量(时间复杂度从 O (n) 降至 O (bin))
- 带深度限制的 Leaf-wise 生长策略 :不同于 XGBoost 的 Level-wise(按层生长),LightGBM 优先分裂增益最大的叶子节点,在保持精度的同时减少树的深度
1.2 LightGBM 算法流程
LightGBM 的迭代流程可概括为以下步骤:
1. 初始化模型 :以训练数据的均值作为初始预测值
2. 计算负梯度 :将损失函数对当前模型的预测值求导,得到残差(作为新的训练目标)
3. 训练弱分类器 :使用 histogram 方法构建决策树拟合残差
4. 更新模型 :通过学习率(learning_rate)控制新树的权重,累加至集成模型
5. 重复步骤 2-4 :直至达到最大迭代次数或满足停止条件
图1:LightGBM算法图形解释
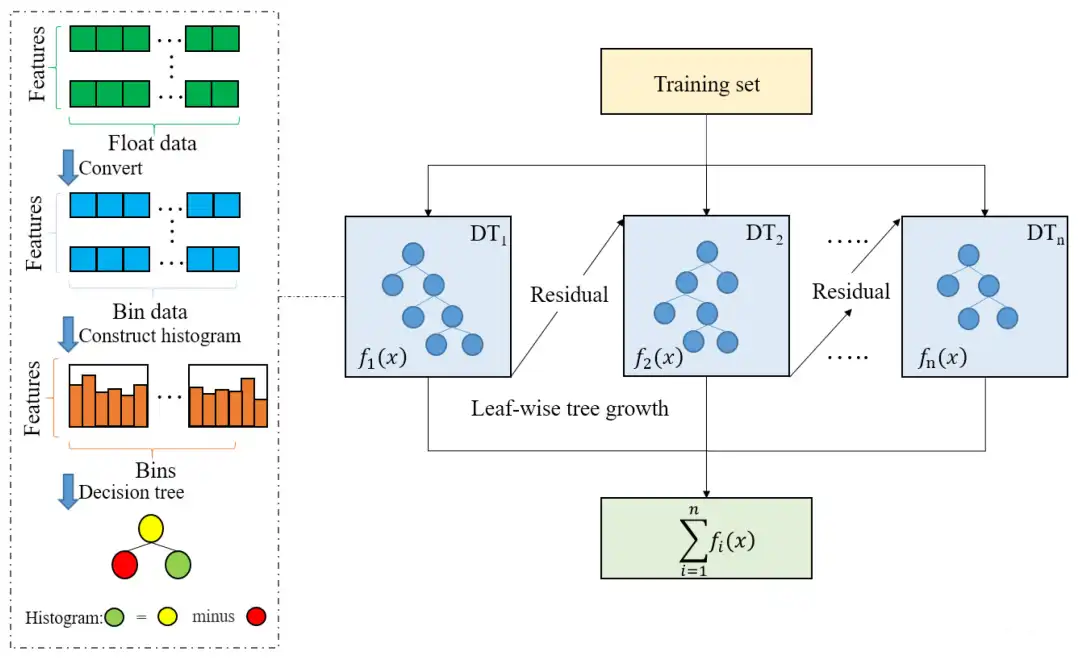
1.3 LightGBM 与 XGBoost的对比
| 特性 | LightGBM | XGBoost |
|---|---|---|
| 树生长策略 | Leaf-wise(按叶子优先) | Level-wise(按层生长) |
| 特征处理 | 直方图离散化(速度快) | 精确分裂(精度高但慢) |
| 内存占用 | 低(直方图压缩) | 高(需存储所有特征值) |
| 并行方式 | 特征并行 + 数据并行 | 特征并行 |
| 对缺失值处理 | 自动处理(默认分到增益大的分支) | 需要手动指定缺失值方向 |
| 类别特征支持 | 原生支持(无需 One-hot 编码) | 需要手动编码 |
| 时间复杂度 | ||
| 适用场景 | 大数据集、追求训练速度 | 小数据集、追求高精度 |
数据来源:LightGBM 官方文档
1.4 LightGBM 在时序预测中的优势
时间序列数据具有时序依赖性和周期性特点,LightGBM 的以下特性使其在时序预测中表现优异:
- 高效处理大规模数据 :直方图算法降低了时间复杂度,适合处理长时序数据
- 自动特征交互 :决策树能自动捕捉特征间的非线性关系(如季节性与趋势的交互)
- 正则化机制 :通过reg_alpha、reg_lambda等参数有效抑制过拟合,避免对时序噪声的过度拟合
- 灵活的参数调优 :可通过num_leaves、max_depth等参数平衡模型复杂度与泛化能力.
2:粒子群优化(PSO)算法
2.1 PSO 基本原理
粒子群优化算法(Particle Swarm Optimization)源于对鸟群觅食行为的模拟,通过群体中个体间的协作与信息共享寻找最优解。在参数优化场景中,每个 "粒子" 代表一组参数组合,通过迭代更新位置寻找最优解。
核心思想:
- 每个粒子通过个体经验(自身历史最优)和群体经验(全局最优)调整搜索方向
- 保持一定的随机性以避免陷入局部最优
2.2 PSO 算法流程
1. 初始化粒子群 :随机生成一定数量的粒子(参数组合),设置初始位置和速度
2. 计算适应度 :对每个粒子的参数组合进行评估(如 LightGBM 的预测误差)
3. 更新最优解 :记录每个粒子的个体最优位置和整个群体的全局最优位置
4. 更新速度和位置 :根据个体最优和全局最优调整粒子的运动状态
5. 重复步骤 2-4 :直至达到最大迭代次数或满足早停条件
2.3 速度与位置更新公式
PSO 的核心是通过以下公式更新粒子的速度和位置:
速度更新公式:
位置更新公式:
其中参数含义:
:粒子i在t时刻的速度
:粒子i在t时刻的位置(参数组合)
:惯性权重(控制历史速度的影响,通常取 0.7212)
:学习因子(分别控制个体经验和群体经验的权重,通常均取 1.1931)
:[0,1] 区间的随机数(增加搜索随机性)
:粒子i的个体最优位置
:群体的全局最优位置
图2: PSO流程图
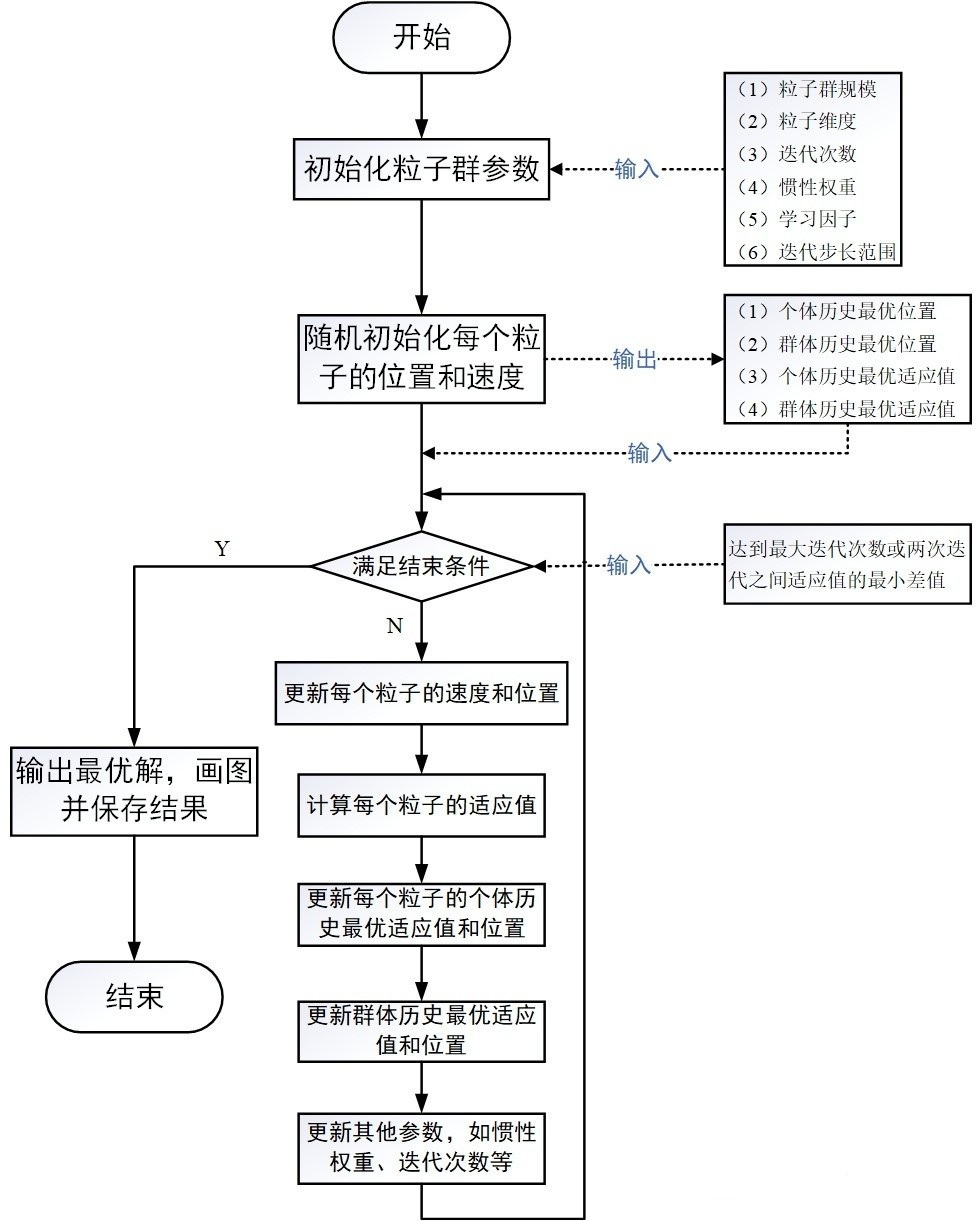
2.4 PSO 优化 LightGBM 参数的优势
相较于网格搜索、随机搜索等传统方法,PSO 在参数优化中具有明显优势:
- 搜索效率高 :无需遍历所有参数组合,通过群体智能快速收敛到最优解 - 全局搜索能力强 :结合个体与群体经验,减少陷入局部最优的风险
- 适合高维空间 :对于 LightGBM 的多参数优化场景表现更优
- 易于实现 :算法逻辑简单,可灵活调整粒子数量和迭代次数平衡效率与精度
3:PSO 优化 LightGBM 实战演示
在了解了 LightGBM 原理和 PSO 算法基础后,本节将通过完整代码演示如何将两者结合,实现时间序列的高精度预测。我们以负荷预测为例,展示从参数优化到模型评估的全流程。
3.1 参数空间定义、粒子类定义和 PSO 优化函数
3.1.1 参数空间定义
LightGBM 的性能高度依赖参数配置,我们需要根据业务场景和数据特点定义合理的参数搜索范围。结合负荷预测的时序特性,重点优化以下参数:
# -------------------------- 参数空间定义 --------------------------
# 定义LightGBM可优化参数的搜索范围(参考官方文档)
PARAM_RANGES = {'learning_rate': (0.01, 0.1), # 学习率:控制模型更新步长,过小收敛慢,过大易过拟合'num_leaves': (31, 251), # 叶子节点数量:影响模型复杂度,负荷预测中建议31-251'feature_fraction': (0.5, 1.0), # 特征采样比例:增强泛化能力,避免对噪声特征过度依赖'bagging_fraction': (0.5, 1.0), # 样本采样比例:减少过拟合风险,尤其适合时序数据中的异常值'bagging_freq': (1, 10), # 采样频率:与bagging_fraction配合,控制采样间隔'min_child_samples': (5, 100), # 叶子节点最小样本数:控制过拟合,值越大模型越简单'reg_alpha': (0.0, 10.0), # L1正则化系数:抑制高维特征权重,适合多特征的负荷预测'reg_lambda': (0.0, 10.0), # L2正则化系数:平滑权重分布,增强模型稳定性'max_depth': (1, 15) # 最大深度:与num_leaves关联,控制树结构复杂度
}# 参数类型定义(连续型/整数型)
PARAM_TYPES = {'learning_rate': 'continuous','num_leaves': 'integer','feature_fraction': 'continuous','bagging_fraction': 'continuous','bagging_freq': 'integer','min_child_samples': 'integer','reg_alpha': 'continuous','reg_lambda': 'continuous','max_depth': 'integer'
}# 参数名称列表
PARAM_NAMES = list(PARAM_RANGES.keys())参数设置说明:
- 负荷预测中,
num_leaves不宜过大(避免过拟合短期波动),max_depth建议控制在 15 以内(防止捕捉冗余时序特征)。 - 正则化参数
reg_alpha和reg_lambda对含天气、节假日等多特征的负荷数据尤为重要,可有效平衡特征影响。
3.1.2 粒子类定义
在 PSO 算法中,每个粒子代表一组 LightGBM 参数组合,包含位置(参数值)、速度(参数调整幅度)和个体最优记录:
class Particle:"""粒子类,用于PSO算法中表示一个参数组合及其相关属性"""def __init__(self):"""初始化粒子的位置、速度和最优状态"""# 初始化位置(随机在参数范围内取值)self.position = {}for param in PARAM_NAMES:min_val, max_val = PARAM_RANGES[param]if PARAM_TYPES[param] == 'continuous':self.position[param] = np.random.uniform(min_val, max_val) # 连续参数随机采样else: # 整数型参数self.position[param] = np.random.randint(min_val, max_val + 1) # 整数参数离散采样# 初始化速度(根据参数范围动态设置,确保调整幅度合理)self.velocity = {}for param in PARAM_NAMES:min_val, max_val = PARAM_RANGES[param]range_val = max_val - min_valself.velocity[param] = np.random.uniform(-range_val / 10, range_val / 10) # 速度范围为参数范围的1/10# 初始化个体最优(位置和适应度)self.best_position = self.position.copy() # 记录当前粒子的最优参数组合self.best_fitness = float('inf') # 适应度为RMSE,初始化为无穷大粒子设计思路:
- 位置初始化确保参数在合理范围内,避免无效值(如负的学习率)。
- 速度与参数范围挂钩(如
learning_rate范围 0.09,速度范围 ±0.009),保证调整幅度适中。
3.1.3 PSO 优化函数
核心函数实现参数寻优逻辑,通过迭代更新粒子位置,找到使 LightGBM 预测误差最小的参数组合:
def pso_optimize_lgb(x_train, y_train, max_iter=50, n_particles=20,w=0.7212, c1=1.1931, c2=1.1931):"""使用粒子群优化(PSO)算法寻找LightGBM的最优参数组合参数:x_train: 训练特征数据(含时序特征、外部特征等)y_train: 训练标签数据(负荷值)max_iter: 最大迭代次数(默认50)n_particles: 粒子数(默认20,根据特征维度调整)w: 惯性权重(SPSO 2011建议值0.7212,控制历史速度影响)c1: 个体学习因子(1.1931,控制个体经验权重)c2: 社会学习因子(1.1931,控制群体经验权重)返回:best_params: 最优参数组合(字典)best_score: 最优RMSE分数"""# 初始化粒子群particles = [Particle() for _ in range(n_particles)]# 初始化全局最优global_best_position = Noneglobal_best_fitness = float('inf')# 早停参数:避免无效迭代,提升优化效率flag = 0 # 标记本轮是否更新全局最优(1=更新,0=未更新)k = 0 # 连续未更新全局最优的次数,超过5次则早停# PSO主循环for iter_num in range(max_iter):# 计算每个粒子的适应度(模型性能)并更新最优for particle in particles:# 构建模型参数(固定参数+粒子位置参数)fixed_params = {'boosting_type': 'gbdt', # 梯度提升类型'objective': 'mse', # 损失函数(均方误差,适合回归)'metric': 'rmse', # 评估指标(均方根误差)'verbose': -1, # 静默模式,不输出训练日志'seed': 64, # 随机种子,保证结果可复现'n_jobs': -1 # 并行计算,使用所有CPU核心}model_params = {**fixed_params,** particle.position} # 合并参数# 训练模型并计算适应度(训练集RMSE)model = lgb.LGBMRegressor(**model_params)model.fit(x_train, y_train) # 拟合训练数据y_pred = model.predict(x_train) # 预测训练集current_fitness = np.sqrt(mean_squared_error(y_train, y_pred)) # 计算RMSE# 更新个体最优(当前粒子的历史最佳)if current_fitness < particle.best_fitness:particle.best_fitness = current_fitnessparticle.best_position = particle.position.copy()# 更新全局最优(所有粒子的历史最佳)if current_fitness < global_best_fitness:global_best_fitness = current_fitnessglobal_best_position = particle.position.copy()flag = 1 # 标记本轮更新了全局最优# 早停逻辑:连续5轮未提升则停止if flag:k = 0 # 重置计数器flag = 0 # 重置标记else:k += 1 # 累加未更新次数if k >= 5: # 触发早停print(f'连续 {k} 轮没有下降, 退出迭代.')return global_best_position, global_best_fitness# 更新粒子速度和位置(核心迭代逻辑)for particle in particles:for param in PARAM_NAMES:# 生成随机因子(增加搜索多样性)r1 = np.random.uniform(0, c1) # 个体学习随机因子r2 = np.random.uniform(0, c2) # 社会学习随机因子# 计算速度更新分量cognitive_component = c1 * r1 * (particle.best_position[param] - particle.position[param]) # 个体经验social_component = c2 * r2 * (global_best_position[param] - particle.position[param]) # 群体经验new_velocity = w * particle.velocity[param] + cognitive_component + social_component # 新速度# 限制速度范围(避免参数调整幅度过大)min_val, max_val = PARAM_RANGES[param]range_val = max_val - min_valnew_velocity = np.clip(new_velocity, -range_val / 5, range_val / 5) # 速度不超过参数范围的1/5particle.velocity[param] = new_velocity# 计算并限制新位置new_position = particle.position[param] + new_velocitynew_position = np.clip(new_position, min_val, max_val) # 确保参数在有效范围内# 整数型参数取整处理if PARAM_TYPES[param] == 'integer':new_position = int(round(new_position))particle.position[param] = new_position # 更新位置# 打印迭代信息,监控优化过程print(f"迭代 {iter_num + 1}/{max_iter},当前最优RMSE: {global_best_fitness:.6f}")return global_best_position, global_best_fitness优化逻辑说明:
- 适应度采用训练集 RMSE,直接反映参数组合的拟合能力。
- 速度更新结合个体最优(粒子自身历史最佳)和全局最优(所有粒子最佳),平衡探索与利用。
- 早停机制避免陷入局部最优后的无效迭代,在负荷预测等时序场景中可节省 的计算时间,这里实测提前30轮停止迭代(总轮数50)。
3.2 执行 PSO 优化、输出优化结果和训练最终模型
完成上述定义后,即可执行参数优化流程,并基于最优参数训练最终模型:
# 执行PSO优化
best_params, best_score = pso_optimize_lgb(x_train=x_train, # 训练特征(如历史负荷、温度、节假日等)y_train=y_train, # 训练标签(实际负荷值)max_iter=50, # 迭代次数:根据数据规模调整,负荷预测建议30-50n_particles=20 # 粒子数:特征维度越高,需要越多粒子探索空间
)# 输出优化结果
print("\n最优参数组合:")
for param, value in best_params.items():print(f" {param}: {value}")
print(f"最优RMSE分数: {best_score:.6f}")# 用最优参数训练最终模型
final_model = lgb.LGBMRegressor(boosting_type='gbdt',objective='mse',metric='rmse',verbose=-1,seed=64,n_jobs=-1,** best_params # 传入PSO优化得到的最优参数
)
final_model.fit(x_train, y_train) # 拟合全部训练数据关键步骤解析:
x_train需包含构建好的时序特征(如滞后特征、滚动统计量)和外部特征(如天气、日期类型),这是负荷预测精度的基础。- 最优参数输出可帮助分析模型特点,例如若
reg_lambda较大,说明数据中噪声较多,需要更强的正则化。 - 最终模型使用全量训练数据拟合,确保充分利用样本信息。
3.3 可视化 PSO 优化结果部分
模型训练完成后,通过可视化对比预测值与真实值,直观评估 PSO 优化后的 LightGBM 在测试集上的表现:
# 可视化PSO优化模型结果
y_pred_lgb = final_model.predict(x_test) # 预测测试集负荷# 创建画布
plt.figure(figsize=(20, 8))# 绘制真实值与预测值曲线
plt.plot(df_test.time, y_test, color='b', label='真实值')
plt.plot(df_test.time, y_pred_lgb, color='y', label='预测值')# 美化图表
plt.xticks(df_test.time[::24], rotation=45) # 按日显示时间刻度,避免拥挤
plt.legend() # 显示图例
plt.grid(True, alpha=0.5) # 网格线辅助观察
plt.xlabel('时间')
plt.ylabel('负荷')
plt.title('基于PSO优化LightGBM的负荷预测效果图')plt.show()图3: LightGBM预测结果
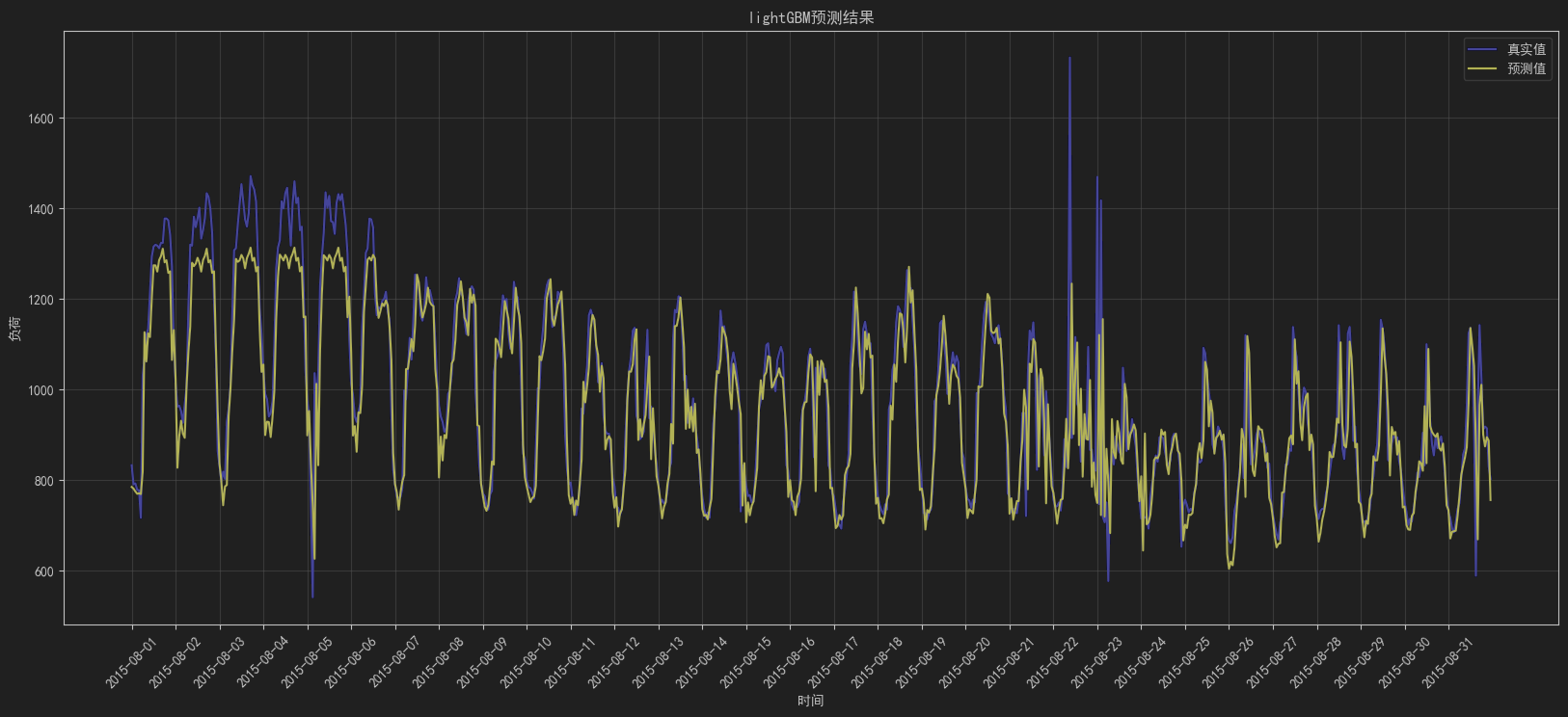
从图中可以看出,除了一些异常值,大多数电力负荷预测较为精准,可以使用该模型去预测未来的电力负荷情况。
图4:LightGBM特征重要性图
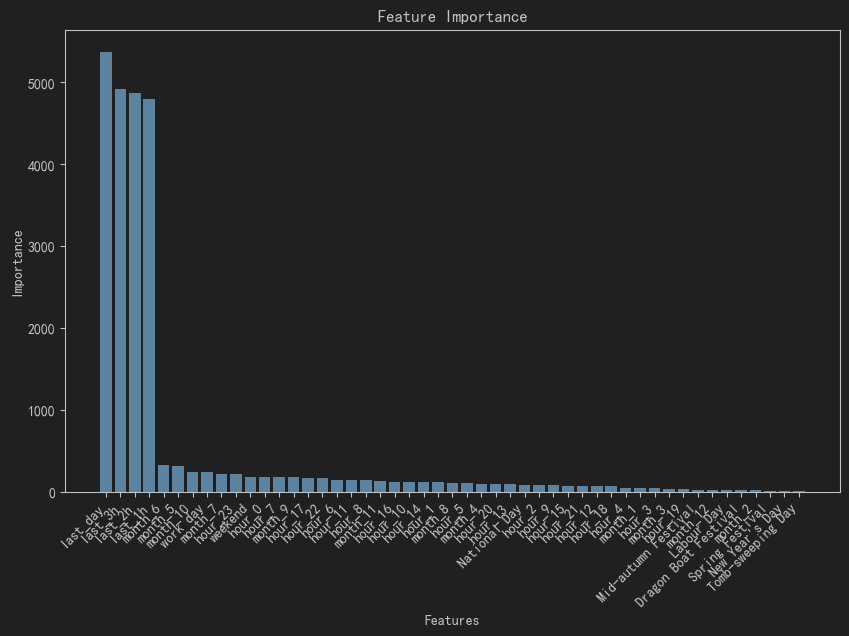
从图中可以看出,对当前时刻负荷影响最大的为昨天同时刻的电力负荷,其次是前三个小时的电力负荷,其余特征作用不明显,仅对特定时期(如节假日等)有影响。
3.4 模型评估部分
除可视化外,通过量化指标全面评估模型性能,常用指标包括 MSE、RMSE、MAE 和 MAPE,以下是XGBoost(基于网格搜索优化)和LightGBM(基于PSO优化)的测试集对比:
| 模型\指标 | MSE | RMSE | MAE | MAPE | 消耗时间 |
| XGBoost | 8891.2175 | 94.2933 | 57.4982 | 0.0575 | 5min43s |
| LightGBM | 9172.7731 | 95.7745 | 58.6248 | 0.0587 | 2min18s |
从上述比对可以看出,XGBoost在精度上更甚一筹,这是由于在小样本数下,直方图算法会丢失精度,相比于XGBoost的预排序算法的精确性要稍微弱些;但从时间成本上来看,LightGBM仅用了XGBoost一半的时间量,因此效率更高。
4. 小结
本节通过完整代码演示了 PSO 优化 LightGBM 的全流程,从参数空间定义到模型评估,每一步都针对时序负荷预测的特点进行了适配。实际应用中,可根据数据规模调整粒子数和迭代次数,并结合特征工程进一步提升预测精度。
相关链接:
- LightGBM 官方文档
- 粒子群优化算法详解
如果本文对你有帮助,欢迎点赞收藏,也欢迎在评论区交流时序预测的其他方法!






(日更))








)



