LeetCode 面试经典 150 题：轮转数组（三次翻转法详解 + 多解法对比）

在数组类算法题中，“轮转数组” 是一道考察 “原地操作” 与 “逻辑转换” 能力的经典题目。所谓 “轮转”，是指将数组元素向右移动指定步数，且超出数组长度的元素需 “循环” 到数组开头。这道题的最优解 ——三次翻转法，能以 O (n) 时间复杂度和 O (1) 空间复杂度实现原地轮转，是面试中高频考察的高效思路。本文将从题目解读、三次翻转法原理、步骤演示，到代码实现，再到其他解法对比，帮你彻底掌握这道题的核心逻辑。

一、题目链接与题干解读

首先，你可以通过以下链接直接访问题目，先自行思考解题方向：

LeetCode 题目链接：189. 轮转数组

题干核心信息

题目要求如下：

给定一个整数数组 nums，将数组中的元素向右轮转 k 个位置，其中 k 是非负数。

例如，若 nums = [1,2,3,4,5,6,7]，k = 3，则轮转后数组为 [5,6,7,1,2,3,4]。

关键注意点

k 的取值范围：k 可能大于数组长度 n，此时轮转效果与 “k 对 n 取模” 后的结果一致（例如 n=7，k=10，10 mod 7=3，轮转 10 步与轮转 3 步结果相同）；

原地操作要求：若想达到最优空间复杂度，需避免开辟新数组，在原数组上完成轮转；

元素顺序保留：轮转后，元素的相对顺序需保持（如示例中 5、6、7 的相对顺序，1、2、3、4 的相对顺序均不变）。

二、核心解法：三次翻转法（原地高效）

三次翻转法的核心思想是 “通过翻转操作，将‘向右轮转’的复杂逻辑转化为三次简单的数组翻转”。其本质是利用翻转对元素顺序的改变，间接实现轮转效果，且全程无需开辟新数组，空间复杂度极低。

1. 为什么需要先对 k 取模？

由于数组轮转 n 步后会回到原始状态（例如 n=7，轮转 7 步后数组不变），因此当 k≥n 时，实际需要的轮转步数为 k_mod = k % n。这一步操作能减少不必要的计算（例如 k=10 时，只需处理 3 步而非 10 步），是优化解题的关键前提。

例如：

当 n=7，k=3 时，k_mod=3，无需调整；

当 n=7，k=10 时，k_mod=10%7=3，按 3 步处理；

当 n=7，k=7 时，k_mod=0，无需轮转（数组不变）。

2. 三次翻转的逻辑原理

我们先明确 “向右轮转 k 步” 的效果：数组末尾的 k 个元素会移动到数组开头，其余元素向右顺延。例如，数组[a1,a2,a3,a4,a5,a6,a7]（n=7），向右轮转 3 步后为[a5,a6,a7,a1,a2,a3,a4]—— 末尾 3 个元素[a5,a6,a7]到开头，前 4 个元素[a1,a2,a3,a4]顺延。

三次翻转法通过以下步骤实现这一效果：

翻转整个数组：将数组从 “前 n-k 个元素 + 后 k 个元素” 的结构，变为 “后 k 个元素的逆序 + 前 n-k 个元素的逆序”；

翻转前 k 个元素：将 “后 k 个元素的逆序” 恢复为原顺序，此时前 k 个元素就是轮转后需要放在开头的元素；

翻转后 n-k 个元素：将 “前 n-k 个元素的逆序” 恢复为原顺序，此时后 n-k 个元素就是轮转后需要放在末尾的元素。

简单来说，三次翻转的逻辑链是：整体翻转打乱顺序→局部翻转恢复目标区域顺序→最终得到轮转结果。

3. 示例演示（以nums = [1,2,3,4,5,6,7]，k=3为例）

步骤 1：计算 k_mod

n=7，k=3，k_mod=3%7=3。

步骤 2：第一次翻转（翻转整个数组）

原数组：[1,2,3,4,5,6,7]

翻转后：[7,6,5,4,3,2,1]

作用：将末尾的 3 个元素（5,6,7）翻转为（7,6,5），移到数组前半部分；将前 4 个元素（1,2,3,4）翻转为（4,3,2,1），移到数组后半部分。

步骤 3：第二次翻转（翻转前 k_mod=3 个元素）

当前数组：[7,6,5,4,3,2,1]

翻转前 3 个元素：[5,6,7,4,3,2,1]

作用：将前 3 个元素（7,6,5）恢复为原顺序（5,6,7），这正是轮转后需要放在开头的元素。

步骤 4：第三次翻转（翻转后 n-k_mod=4 个元素）

当前数组：[5,6,7,4,3,2,1]

翻转后 4 个元素：[5,6,7,1,2,3,4]

作用：将后 4 个元素（4,3,2,1）恢复为原顺序（1,2,3,4），这正是轮转后需要放在末尾的元素。

最终结果与题目预期完全一致，验证了三次翻转法的正确性。

4. 翻转操作的实现

翻转数组的某一段（从索引 left 到索引 right）是三次翻转法的基础操作，实现逻辑如下：

初始化两个指针，left 指向段的起始索引，right 指向段的结束索引；

交换 left 和 right 指向的元素，然后 left 向右移动 1 位，right 向左移动 1 位；

重复上述操作，直到 left ≥ right（即指针相遇或交叉，段内元素全部交换完毕）。

例如，翻转数组[7,6,5]（left=0，right=2）：

交换 7 和 5 → [5,6,7]，left=1，right=1；

left ≥ right，翻转结束。

三、其他常见解法（对比参考）

除了三次翻转法，“轮转数组” 还有其他解法，虽然复杂度不如三次翻转法最优，但能帮助我们从不同角度理解问题，以下简要介绍两种：

1. 额外数组法（空间复杂度 O (n)）

思路

开辟一个与原数组长度相同的新数组，将原数组中 “需要轮转的元素” 按目标顺序放入新数组，最后将新数组的值复制回原数组。

对于原数组索引 i 的元素，轮转后在新数组的索引为 (i + k) % n（向右轮转 k 步）；

也可直接定位：新数组前 k 个元素对应原数组末尾 k 个元素（索引 n-k 到 n-1），新数组后 n-k 个元素对应原数组前 n-k 个元素（索引 0 到 n-k-1）。

优缺点

优点：逻辑直观，易于理解和实现，无需复杂的翻转操作；

缺点：需要开辟额外数组，空间复杂度为 O (n)，不如三次翻转法高效。

2. 多次右移法（时间复杂度 O (nk)）

思路

每次只将数组向右轮转 1 步，重复 k 次。轮转 1 步的逻辑是：保存数组最后一个元素，然后将其余元素从后向前依次右移 1 位，最后将保存的元素放到数组开头。

优缺点

优点：逻辑简单，无需复杂算法，仅需基础的元素移动操作；

缺点：时间复杂度为 O (nk)（每次轮转 1 步需 O (n) 时间，共 k 次），当 k 较大时（如 k=n），时间复杂度会达到 O (n²)，效率极低。

四、复杂度分析（三次翻转法）

1. 时间复杂度：O (n)

翻转操作的时间复杂度：翻转一段长度为 L 的数组，需要交换 L//2 次元素，时间复杂度为 O (L)；

三次翻转的总时间：第一次翻转整个数组（O (n)），第二次翻转前 k 个元素（O (k)），第三次翻转后 n-k 个元素（O (n-k)），总时间为 O (n) + O (k) + O (n-k) = O (n)；

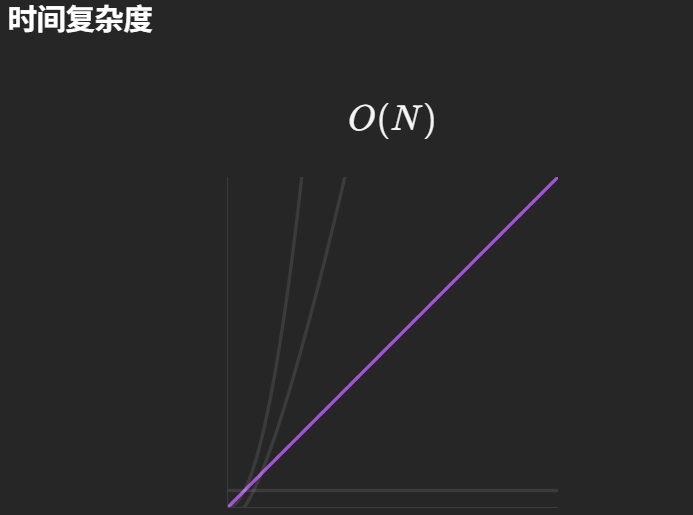
整体时间：加上 k 取模的 O (1) 操作，总时间复杂度为 O (n)。

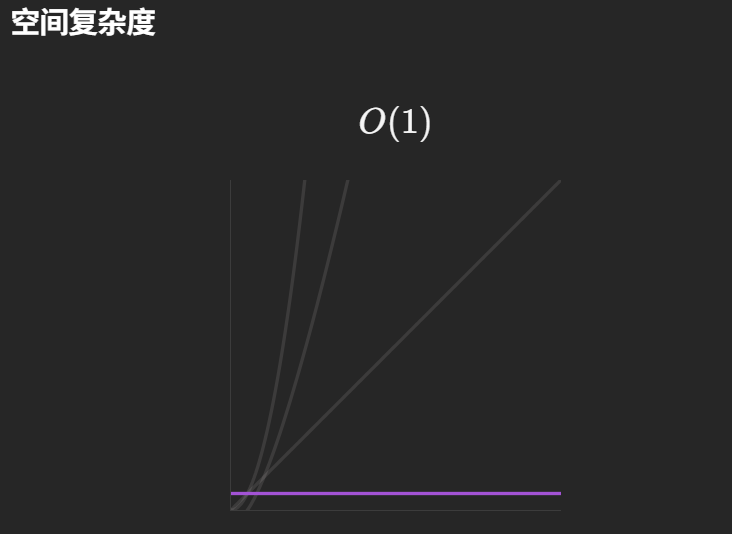
2. 空间复杂度：O (1)

整个过程仅用到了几个额外变量（如 left、right 指针，k_mod 等），没有开辟新的数组或其他数据结构；

所有翻转操作都在原数组上完成，额外空间的使用与数组长度 n 无关，因此空间复杂度为常数级的 O (1)。

五、三次翻转法代码实现

以下以 Python，Java 为例，实现三次翻转法，核心是先实现 “段翻转” 函数，再执行三次翻转：

1，Python

class Solution:def rotate(self, nums: List[int], k: int) -> None:def reversed(i: int, j: int):while i < j:nums[i], nums[j] = nums[j], nums[i]i, j = i + 1, j - 1n = len(nums)k %= nreversed(0, n - 1)reversed(0, k - 1)reversed(k, n - 1)

2，Java

class Solution {int[] nums;public void rotate(int[] nums, int k) {this.nums = nums;int n = nums.length;k %= n;reversed(0, n - 1);reversed(0, k - 1);reversed(k, n - 1);}private void reversed(int i, int j) {for (; i < j; i++, j--) {int t = nums[i];nums[i] = nums[j];nums[j] = t;}}
}

你可以将上述代码复制到 LeetCode 编辑器中测试，完全符合题目要求。