中国古代数学符号的演进 | 算筹 / 符号 / 算法

注：本文为“中国古代数学符号”相关合辑。

图片清晰度受引文原图所限。
略作重排，未整理去重。
如有内容异常，请看原文。

这个中国古代的数学瑰宝，到底厉害在哪？

原创朱一文科普中国 2024 年 07 月 31 日 15:30 北京

中国古代数学源远流长，《九章算术》作为汉代成书的重要数学著作，历来被称作“算经之首”。已故中国科学院院士、著名数学家吴文俊先生（1919-2017）曾指出：“《九章算术》及其刘徽注，在数学发展史上具有崇高的地位，足以与古希腊欧几里得《几何原本》东西辉映，各具特色。”那么，《九章算术》究竟有哪些数学成就，又为何在数学史上有如此高的地位呢？

算筹与准十进制位值制记数法

《九章算术》总结了先秦以来的数学成就，其中最重要的数学成就是算筹的准十进制位值制记数法。所谓十进制（decimal system），是从 1 开始记数，到 10 换一个记数方式；而位值制（place - value system）是指同一个数字放在不同位置，具有不同的数量含义。古埃及数学采用十进制记数法，但并非位值制（而是垒数制）；古巴比伦数学采用位值制记数法，但使用的是 60 进制。现代的印度 - 阿拉伯数字是十进制位值制，而从文献记载来看，其晚于中国算筹记数。因此，新加坡学者蓝丽蓉（Lam Lay Yong）甚至提出印度 - 阿拉伯数字可能起源于中国算筹的说法。2016 年，中国科学院自然科学史研究所编写的《中国古代重要科技发明与创造》一书，明确将这一成就列入其中。

算筹在中国使用了约 2000 年，直到 16 世纪被算盘取代之前，一直是中国人长期使用的数学工具，也是日本、朝鲜、越南、琉球等汉字文化圈国家长期使用的数学工具。其材质通常为竹子（也有象牙、骨、铅、银等），汉代的算筹长约 12 厘米。近代以来，多地有算筹出土，例如 1983 年 11 月在陕西省旬阳地区汉墓出土了 28 根象牙算筹。日本也藏有算筹。在古语中，“筭”与“算”不同，前者指摆弄竹子，即算筹；后者指装算筹的器物，引申为计算。因此，古书中普遍写作“筭术”（即运用算筹的算法），例如《九章筭术》。


陕西旬阳出土算筹	日本东大寺所藏算筹

算筹记数分为纵横两式，个、百、万等位上用纵式，十、千、百万等位上用横式。例如，数字 12345 摆放为 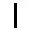12345 的算筹表示。由于十位上的 1 和个位上的 1 摆放不同，因此这种记数法被称为“准位值制”。这一特点体现了算筹记数的优势：遇 0 作空位处理，纵横不同的摆放方式可以最大限度凸显空位，例如 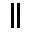203 的算筹表示表示 203，而不可能是 23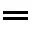（ 23 的算筹表示 )。《九章算术》卷八方程涉及正负术，通过算筹的颜色和摆放方式也可以区分正负。

正负术示意图

以算法为中心

《九章算术》全书分为九卷，包含 246 个数学问题。学界曾存在误解，认为该书是一本应用问题集，但实际上，246 个问题对应的算法（即“术”）仅有约 100 个，多个问题往往对应一个算法。因此，数学史家郭书春指出，该书采用的是“术文统率例题”的形式。另有误解认为该书是一本算法操作手册，运筹者无须理解其中的数学原理。然而，数学史家李继闵指出，算法实施过程中蕴含着算理（即“寓理于算”），不懂数学原理实际无法进行计算。

吴文俊先生指出，中国古代的算法具有构造性和机械化的特点。构造性与现代存在性数学相对应，指算法往往给出求解路径；机械化则体现在筹算过程。法国学者林力娜（Karine Chemla）通过大量文献分析，指出《九章算术》及其刘徽注的数学问题、图和棊等几何工具以及算筹的实施，都是展现算法的工具，从而有力地证明了以《九章算术》为代表的中国古代数学是以算法为中心的数学。从世界数学史角度看，除了古希腊数学以外的其他数学文明都具有算法倾向，丹麦数学史家休儒（Jens Høyrup）进一步认为中国数学是所有文明中最重视算法的。学界以往多认为《九章算术》具有实用性和社会性的特点，其实这一特点其他数学文明也具备，唯有对算法的高度重视是中国古代数学的独特之处。就此而言，《九章算术》可视作一本理论数学著作。

《九章算术》各卷内容如下：

卷一方田：给出筹算分数的计算法则和各种田面积的计算公式，其中圆面积公式为“半周乘半径得积步”，即 $\pi r^2$ ，这一公式巧妙地回避了圆周率，是完全准确的。
卷二粟米：给出各种谷物的换算，其中提出“今有术”，即已知三个数求成比率的第四个数，这一算法在西方被称作“三率法”。
卷三衰分：讲述各种物品的比例分配问题。
卷四少广：涉及土地的丈量和划分，给出用算筹开平方和开立方的算法，这一方法在宋代发展成普遍求任意一元高次方程数值解的算法，与现代数学中的牛顿法类似。
卷五商功：处理工程问题，涉及各种几何体的体积计算问题，提出三种基本几何体（立方、堑堵和阳马）作为求解任意几何体体积的基础。立方即正立方体；堑堵是底面为等边直角三角形的三棱锥，两堑堵合成一立方；阳马是底面为正方形，一棱与底垂直的四棱锥，三阳马合成一立方。
卷六均输：关于税收的比例分配问题。
卷七盈不足：通过两次假设求解问题的算法，该算法在西方被称作“双假设法”。由于该法可以把任何问题理解成线性问题，进而求出解答，故也称为万能算法。
卷八方程：求解多元一次线性方程组的完整算法，其中给出涉及该问题时必须用到的正负术法则。例如第一问：

今有上禾三秉，中禾二秉，下禾一秉，实三十九斗；上禾二秉，中禾三秉，下禾一秉，实三十四斗；上禾一秉，中禾二秉，下禾三秉，实二十六斗。问：上、中、下禾实一秉各几何？答曰：上禾一秉九斗四分斗之一，中禾一秉四斗四分斗之一，下禾一秉二斗四分斗之三。

按术列出如下方程，其求解过程类似现代的矩阵方程解法。清末现代数学传入中国后，李善兰借用古语“方程”翻译“equation”，实际改变了方程的原意。
卷九勾股：讲述平面图形的面积计算问题，给出勾股定理及其各种变化形式。

给出算法正确性的论证

刘徽注《九章算术》

《九章算术》文本中只给出算法，而没有其正确性的证明。这一特点曾被用作中国数学不如以《几何原本》为代表的古希腊数学的论据，但现代数学史研究已证明这一观点站不住脚。首先，除了古希腊数学以外的数学文明，往往只给出算法而没有证明。吴文俊先生认为数学史是算法倾向与演绎倾向两大主题此消彼长形成的。其次，文本中是否有证明取决于文本的性质和语境，文本中没有证明并不代表数学实践中也没有证明。最后，林力娜等学者认为不应以古希腊的数学证明作为证明的唯一形态，其他文明中也有不同形态的证明。刘徽注可以验证这后两点。

魏景元四年（263 年），刘徽注解了《九章算术》，对大部分术文都给出其算法正确性的论证。例如，在卷一对圆面积公式的证明、卷四对球体积公式的注解、卷五对阳马体积的证明中，刘徽用到极限逼近的推理方法，展现了极高的逻辑推理能力。在卷四求解球体积公式的过程中，刘徽发明出牟合方盖，但无法求出其体积，故“以俟能言者”。这一问题最终被祖冲之父子解决。刘徽对几何问题的证明需用到图（平面问题）和棊（立体问题），其推理原理被吴文俊总结为“出入相补原理”。

《九章算术》的影响与历史地位

《九章算术》在唐宋时期均为国子监算学馆的教科书。刘徽之后，唐李淳风、北宋贾宪、刘益、蒋周、南宋秦九韶、杨辉、金李冶、元朱世杰等均沿着《九章算术》的路线发展中国古代数学，并使其在宋元时代达到一个高峰。明清时期，中国数学发展的主流虽发生改变，但《九章算术》的整体框架并未改变。日本数学则在中国宋元数学的基础上发展出和算，在 19 世纪时可以处理面积求和等微积分初等问题。

自李俨（1892-1963）、钱宝琮（1892-1974）先生开创中国数学史研究以来，《九章算术》及其后世注解就作为中国数学成就的标志性著作。他们主要关注其中与现代数学相通之处，但实际上，《九章算术》中那些独特算法同样是中国数学的伟大成就。两者共同说明了中国数学历史道路的独特性和其历史经验的有效性。

吴文俊先生将中国古代数学的算法理解成计算机的软件，将算筹、算盘等工具理解成计算机的硬件，从而创造性地提出数学机械化的构想，这是中国古代数学“古为今用”的典范案例。

策划制作

本片为科普中国・创作培育计划扶持作品
出品丨中国科协科普部
监制丨中国科学技术出版社有限公司、北京中科星河文化传媒有限公司
作者丨朱一文科学技术史博士，中山大学哲学系教授、博士生导师，逻辑与认知研究所专职研究员
策划丨林林
责编丨林林钟艳平
审校丨徐来

从刻痕与结绳到现代数学符号，人类如何创造语言的另一种奇迹

原创遇见数学科学演绎法 2024 年 11 月 27 日 20:05 河南

数学是一种独特的语言，它以简洁而精准的符号揭示自然规律，并帮助人类探索不可见或抽象的领域——从微观粒子到宏观宇宙，从无穷到高维空间，甚至复杂的逻辑结构。数学符号的诞生与发展是人类智慧的结晶，也是科学和技术进步的基石。今天，我们走近数学符号的世界，了解它是如何诞生、如何运作，以及为什么它如此重要。

数学符号的重要性

数学符号是用来表示数学对象、运算、关系和逻辑规律的符号体系，包括数字、变量与常量、运算符、关系符及各个不同数学分支中的特殊符号。数学符号的力量在于其简洁性和通用性。它超越了语言的障碍，成为科学家、工程师和数学家共同的交流语言。

爱因斯坦的著名公式 $E = mc^2$ 是一个典型例子。当爱因斯坦提出质量和能量之间的关系时，他借助这一公式，将一个复杂的物理概念浓缩成简短的表达式。没有这些符号，就需要用一整段话甚至几页文字来描述这个等式的含义。

数学符号不仅简洁，还具有通用性。无论是中国人、法国人还是印度人，公式 $E = mc^2$ 或 $a^2 + b^2 = c^2$ 的意义都是一致的。数学符号超越了语言和文化的障碍，成为全球通用的交流思想的工具。

不仅如此，数学符号还具有抽象性，能够描述自然语言难以企及的深刻概念和复杂逻辑。例如，逻辑表达式 $\forall \; x \in \mathbb{R}, \exists\; y \in \mathbb{R}, y > x$ 用符号精确地表达了“对于任意一个实数 $x$ ，总存在一个比它大的实数 $y$ ”的数学思想。这种抽象能力使得数学不仅可以研究具体的对象，还能深入研究逻辑关系、集合结构甚至高维空间的性质。

数学符号的价值还在于其普适性。它不仅是科学研究的工具，更是思想的载体。正是通过这些符号，数学家得以将复杂的概念形式化，进而探索更远的未知领域。

数学符号的起源与演化

数学符号的演化史是人类智慧发展的缩影。从最早的计数工具到今天复杂的公式，数学符号经历了漫长而有趣的发展过程。数学符号的历史可以追溯到人类文明之初，随着人类对数学的理解不断深化，符号才逐渐被抽象和系统化。

早期的计数和符号萌芽

数学符号的历史可以追溯到数万年前。当时，所谓的数学活动主要是计数，最古老的数学工具是简单的刻痕、结绳或小石头，这些原始的符号虽然简单，但标志着人类开始尝试用外部工具记录和表达数学思维。

在这里插入图片描述

例如：

伊尚戈骨（约 20,000 年前）：一块来自非洲的骨头，上面刻有规律的刻痕，被认为可能是早期的计数工具。
绳结记事法：安第斯山脉的印加文明使用“结绳”记录数字和信息，这种方法被称为“基普”。

随着文明的进步，数字符号逐渐出现。巴比伦人发明了用楔形文字记录数字的方式，发明了基于 60 进制的计数系统。而古埃及人则用象形符号表示数量。这些早期符号尽管原始，却标志着数学思维的萌芽。

零的出现：数学符号史上的里程碑

数位的概念和零的发明是数学符号发展史上的重要一步。因为在此之前，零的概念并不存在。

巴比伦人（约公元前 2000 年）：最早使用零作为占位符。例如，数字 306 中的“0”表示“没有十位数”。
印度数学家（约公元 5 世纪）：率先将零视为一个独立的数字，并用点或圆圈表示。这一创新被阿拉伯数学家传播到全世界，极大推动了数学的发展。

在这里插入图片描述

零的出现不仅解决了数字记录的难题，还为现代数学、科学和工程领域奠定了基础。没有零，代数、微积分乃至计算机科学的发展都将无从谈起。

16 世纪：数学符号化的转折点

数学符号的系统化发展始于文艺复兴时期。在 16 世纪之前，数学的表达方式与今天我们熟悉的符号化数学有着天壤之别。几乎所有的数学思想、计算步骤和证明过程都通过自然语言叙述，而不是符号化的表达。例如，古希腊数学家欧几里得在《几何原本》中使用长篇叙述来陈述几何定理，而非符号化的表达方式。

在这里插入图片描述

正是在这种背景下，部分数学家尝试用更简洁的形式表达数学思想。其中，丢番图（Diophantus） 是重要的先驱之一。他的著作《算术》（Arithmetica）中，开创性地引入了一些符号化的方法，以简化数学表达：

用符号表示未知数。例如，丢番图用一种特殊的符号（类似希腊字母）来表示未知数，而不是用完整的文字描述。
使用缩写表示某些数学运算。例如，他用一种简写的形式表达平方和平方根运算，而不是通过详细的句子。

这标志着数学符号化的早期尝试。然而，由于丢番图的符号体系并未被广泛传播，因此直到文艺复兴时期，这种符号化的思想才被再次发展和推广。

现代数学符号的诞生

在这里插入图片描述

数学符号的系统化始于文艺复兴时期：

弗朗索瓦・韦达（François Viète）（16 世纪）：首次使用字母表示未知数，开创了代数学符号化的先河。
笛卡尔（René Descartes）（17 世纪）：引入了我们今天熟悉的符号，比如用 $x, y, z$ 表示未知数，用 $a, b, c$ 表示已知量。他还提出了复数单位 $i$ 的概念。

18 至 19 世纪的标准化

莱布尼茨与牛顿：分别提出了微积分的符号体系。莱布尼茨的积分符号 $\int$ 和微分符号 $d$ 至今仍在使用。
随后，欧拉（Leonhard Euler） 在 18 世纪对数学符号进行了进一步的完善。他发明或推广了许多我们今天熟知的符号，例如函数表示法 $f (x)$ 、自然对数的底数 $e$ 和圆周率 $\pi$ 。

随着数学的全球化传播，符号逐渐被标准化。统一的符号体系不仅缩短了数学家之间的交流时间，还推动了数学思想的迅速传播。

尽管数学符号的基础体系在 18 世纪已经确立，但发展并未停止。随着探索数学的不断深入，许多新符号还在引入以应对复杂的数学需求。

现代符号的扩展

随着数学分支的扩展（如拓扑学、统计学和量子力学），新的符号也不断被创造出来。例如，拓扑学中，符号 $\partial$ 描述了边界运算；量子力学中使用了狄拉克符号（如 $\psi \rangle$ 和 $\langle \psi |$ ）来表示量子态。

结语：数学符号的魅力

数学符号是人类智慧的结晶。它不仅是科学交流的工具，也是我们探索世界奥秘的钥匙，是人类文明进步的缩影。当你下次看到复杂的数学公式时，不妨换个视角。试着去理解这些符号背后的故事和逻辑，它们不是冷冰冰的字符，更是通往知识殿堂更深处的桥梁。

位置示数法：一种具有代数符号功能并具优势的中国传统数学方法

邹大海、夏庆卓返朴 2025 年 02 月 16 日 08:30 北京

代数符号的引入与使用，对数学的发展具有重大的促进作用。中国古代的筹算采用了一种位置示数法，具有代数符号的功能。它不仅借助位置来表示数，而且用位置来表现各种未知数及其不同次数的幂，还利用相对位置的调整来实现代数运算的功能，且在某些方面更具优势，充分展现了中国传统数学的特色。将中国传统数学的位置示数法与现代数学的符号代数法结合，有可能为数学的发展提供新的思路。

撰文 | 邹大海（中国科学院自然科学史研究所）、夏庆卓（中国科学院自然科学史研究所、中国科学院大学）

用代数符号来表示未知量或可变量，对于数学的发展具有重要的意义。[注释 1] 成套的数学符号是 16 世纪以来在欧洲首先发展起来的 [1]。在西欧数学传入以前，中国传统数学很少使用代数符号，但代数学却是很发达的。究其原因，中国古代的哲人充分发掘位置在数学中的重要作用 [注释 2]，开发出了一套用位置标示数学含义的方法，可以实现后来近现代数学中代数符号的功能 [注释 3]，这种方法我们称为位置示数法。之所以不称 “位置代数法”，是因为古代并不是让一个位置本身一定代表一个数或未知量，而只是强调这个位置被用来赋予在该位置或其附近位置上所放置的数据的含义。位置示数法，不仅造就了最早的十进位值制记数法，而且利用位置标示不同的未知数或未知数的幂，进而通过简单操作实现代数运算的功能。本文揭示，比之近现代数学中的代数符号及其运算，中国古代的位置示数法还未发展出那么丰富的功能，就已经在相当长的时期内失传，但它在某些方面却更具优势。本文提出，将中国传统数学中充分发挥位置功能的思想和方法与现代数学的符号表示法结合起来，借助现代计算机技术，或许可以为现代数学的发展提供新的思路，从而为中华优秀传统科技文化在新时代的弘扬，提供一个新的契机。

1 算筹与筹算

中国传统数学对位置的开发利用，始于算筹记数法。算筹是中国古代长期用来记数和计算的工具。古人用算筹来进行记数、表示数量关系，并进而以此为基础进行演算。这些使用算筹的活动和相应的方法，叫做筹算。位置示数法，就是基于筹算语境而发展起来的数学方法。当然，这种方法后来也在珠算中发挥作用。

算筹又称算、筹、策、筹策、算子等。算筹本身非常简单，就是长条形小棍，材质有竹、木、金属、骨头乃至象牙等，但主要是竹和木，尤以竹质为多，所以表示算筹的字往往从竹。

算筹记数包括两个方面。一方面，用算筹表示 1-9 的基本数字时，有纵、横两种形式：

表 1

其中，对于 1 至 5，表示几就用几根算筹；对于 6 至 9，用一根放在上面的算筹表示所含的 5，比 5 多几就在下面用几根算筹与表示 5 的算筹垂直靠拢放置。另一方面，用算筹表示十进制整数时，个、百、万等奇数位用纵式，十、千、十万等偶数位用横式，纵、横交错摆放。若某位上数字为零，则空出相应的位置。如 68012 用算筹表示即 [2, 4-7]。此外，古人席地而坐，个位数字摆放在右膝盖正前方的位置，这样就可以很方便地对末几位全为零的数（如 560、5600）进行区分。

算筹记数可以追溯到原始社会以草茎、小棍记数，上述算筹记数制度应出现于西周和春秋之交而可能更早。这种记数法，只用 9 套符号（每套纵、横 2 个，同一数字横式和纵式视为一个的话则只是 9 个符号）就可以表示任意的自然数，是世界上最早的典型的十进位值制记数法。除符号形式外，它与今天的印度 - 阿拉伯数字记数法相同，而早于后者至少数百年。不仅如此，古人还通过算筹的颜色（红、黑）、形状（截面为三角形、长方形）或摆放方式等来表示正负数。[2, 4-7]

2 位置的数值功能

前面已经说到，中国古代的算筹记数法采用十进位值制。在这记数系统中，同一个数字符号 $a$ 放在不同的数位，表示不同的数值：在个位表示 $a$ ，在十位表示 $a$ 个十，在百位表示 $a$ 个百。数字摆放所处的位置，标示相应的数字单位，这是位置在中国古代数学中最常见和直观的功能，它也一直沿用于现代的世界各地。当然，中国古代的算筹记数法所摆成的符号与印度 - 阿拉伯数码形状不同，而后者在不同时代和地区的写法，也有所变化。

3 位置的未知量功能

中国古代数学中，位置也具有标识未知数的功能。当然，这种功能是通过一定的规则来实现的。首先看现在常用的线性方程组及其解法，中国古代早在两千多年前就有相应的列法和解法，就称为 “方程”，《九章算术》专设第八章 “方程” 章来处理这类问题。不过，古人不用符号表示未知数，而是用不同的位置来体现不同的未知量或常数。如第一题是：

今有上禾三秉，中禾二秉，下禾一秉，实三十九斗；上禾二秉，中禾三秉，下禾一秉，实三十四斗；上禾一秉，中秉二秉，下禾三秉，实二十六斗。问：上、中、下禾实一秉各几何？[9]

其中 “秉” 是量词，表示把、束。“禾” 是从田间粟的植株收割下来带有茎叶和谷穂的部分，“实” 是从禾上打下来的谷子。这个问题假设有上、中、下三等禾，已知它们的秉数的 3 种组合，各得到已知数量的谷子（体积），要求出每等禾一秉分别能打下多少谷子。按现代的方法，可设每秉上等禾、中等禾和下等禾打出的谷子分别为 $x$ 斗、 $y$ 斗和 $z$ 斗，那么由题设中每组已知条件可分别列出一个代数方程式。把 3 个代数方程式联立起来，就得到一个线性方程组：

$\begin{cases} 3x + 2y + z = 39 \quad(1)\\ 2x + 3y + z = 34 \quad(2)\\ x + 2y + 3z = 26 \quad(3) \end{cases}$

《九章算术》用算筹将三个等量关系表示成右、中、左三列数，形成一个方程，如图 1-1；如果把算筹符号换成现代的印度 - 阿拉伯数字，便得到图 1-2。可以看出，只要把图 1 的竖列变成横行，则与现代的增广矩阵并无二致。所以古代的方程是一种采用类似于现代增广矩阵的简单形式，它只用几组数就构成一个整体，这个整体对应于一个联立线性方程组。

这种表示法的核心是将等量关系中的具体数字按特定的顺序进行排布：

（1）各个等量关系中诸未知量的倍数（即现代数学中未知量的系数），在摆放到表示这些等量关系的各列中时都具有相同的顺序。按现代的说法，就是将各列中 $x$ 、 $y$ 、 $z$ 的系数都分别放置于从上至下的第一、二、三个位置。可见，各系数所处的位置具有表示相应未知量的功能。

（2）各个等量关系中的常数项总是放在对应列中的最下位置。也就是说，最下位置具有标示常数项的功能。

因此，尽管当时没有使用未知量的符号，也没有把常数项与未知项用可见的符号区分开来，却通过无形的位置把它们都标识了出来，实现了近一千七八百年以后才采用的代数符号的功能。这种 “方程” 的表达方式与欧洲两千年后用分离系数法表示线性方程组的增广矩阵在形式和结构上都极为相似。不仅如此，中国上古时代 “方程” 的求解变换，与增广矩阵的变换也是非常相似的。古代 “方程” 是增广矩阵的一个太过早熟的先驱。法国科学院院士、曾任苏黎士大学数学系主任的 P. Gabrieal 编写的教科书《矩阵、几何、线性代数》（Matrizen, Geometrie, Lineare Algebra）第 2 节题为 “方程算法”（Der Fang-Cheng Algorithmus），将处理线性方程组的增广矩阵方法称为 “方程法”（Fang-Cheng-Regel），取代了以前的流行称谓 “高斯消元法” [10]。另外，正是由于 “方程” 这种特殊的结构与表达方式，导致了中国早在战国时代就引入了正负数概念，并能顺利地进行正负数的四则运算，而没有陷入欧洲直到 19 世纪还存在的关于负数合法性的纠结中。[7, 11]

4 位置指示未知数的幂

对于一元多项式或一元高次方程，中国古代不用未知数符号，自然也就没有符号来表示未知数的幂。古人想到的办法，还是通过位置来区分。他们将表示某个数的算筹放置在特定的位置，来表明它是未知数若干次幂的倍数（或标示它为常数项）。例如在宋金元时期，对于一元高次方程，通常将常数项、一次项、二次项直到最高项的系数从下至上排列（也有反过来排列的）就可以把它表示出来。

也就是说，从下至上的位置对应着已知数（常数，按现代的说法也可以说是未知数的 0 次方）、未知数的一次方、未知数的二次方、…、未知数的最高次方。而一个位置上放着表示某数的算筹，表示这个数与该位置表示的未知数的幂相乘，

或表示放在该位置的数为已知数（也可以说是该数与未知数的 0 次方相乘）。图 2-1 是《测圆海镜》卷 3 第 5 题的算草中列出的带从开方式，把算筹符号改为印度 - 阿拉伯数字后即图 2-2，相当于一元三次方程 $x^3 - 336x^2 + 5184x + 2488320 = 0$ 。如果有必要，古人也在标示一次项的位置的旁边放置一个 “元” 字或在常数项的旁边放置一个 “太” 字 [5]，以避免混淆，这是方程式在当时的筹算表达式中唯一出现的符号，它们是数学符号但不能算是代数符号，它们与现代的代数符号只有一点点相似。因为，无论是 “元” 字还是 “太” 字，都并不表示具体的某个数或某个未知数，它们只是标示它旁边的位置（而不是它自己所在的位置）上所放的数是一次项或常数项。

在对应于一元三次方程式 $x^3 - 336x^2 + 5184x + 2488320 = 0$ 的筹算表达式图 2-1 中，在一次项系数（从下往上第 2 个数）的旁边放一个 “元” 字就得到图 3-1，在常数项（最下位置）的旁边放置 “太” 字就得到图 4-1。需要注意的是，这里的 “元” 字或 “太” 字，在当时的筹算操作中，是写在一个卡片上的，解题者可以随时根据需要移动它。

5 一个操作，一组运算

位置标示未知量或其幂的方法，不光比符号表示法简单，而且在计算过程中具有相当的优势。比如，上述图 3-1 表示的一元三次方程式 $x^3 - 336x^2 + 5184x + 2488320 = 0$ ，如果方程两边同时乘以 $x$ ，在把每一项都乘以 $x$ 时，用现代的代数

符号表示法需要把每一项都重新写一遍，得到 $x^4 - 336x^3 + 5184x^2 + 2488320x = 0$ ，而中国古代就简单多了，只需要将 “元” 字卡片向下移动一位就可以表示出来（图 5）；如果是将原方程两边除以 $x$ ，现代的符号表示法需要把每一项重新写一遍，

成为 $x^2 - 336x + 5184 + \frac{2488320}{x} = 0$ ，而中国古代则只需把 “元” 字向上移一位即可（图 6）。实际上，如果要乘以（除以） $x$ 的 $n$ 次方，则只要将 “元” 字向下（向上）移动 $n$ 位即可。这种简单的数学操作，比今天利用代数符号做运算，有很大优势：一是不需要每一项都写，要省事得多也简单得多；二是更不容易出错。可见，古代这种移动位置的简单操作，相当于方程的每一项都乘以或除以未知数的幂，起到了进行一组运算的功效；而且方程的项数越多，其优势就越明显。同样地，古人有时不用 “元” 字标识未知数的一次项，而是用 “太” 字标识常数项，也可以通过移到 “太” 字的位置来做类似的乘除运算。

除了多元一次方程组和一元高次方程，宋金元时期的数学家发展出二元、三元和四元的高次方程组。如元代数学家朱世杰利用下、左、右、上四个方向上不同的位置，标示天（ $x$ ）、地 ( $y$ )、人 ( $z$ )、物 ( $w$ ) 四个未知数的相应次数的幂以及它们的乘积（如图 7 所示），从而利用具有分离系数法功能的位置示数法可以表示多至四个未知数的多元高次方程组，并通过 “上升下降”、“左进右退”、“剔而消之”、“余筹易位” 之类的操作，进行消元和变换，予以求解。

中国古代数学充分发掘了位置的功能，不仅有位值观念，还用来表示未知数和它们的幂及其乘积，取得了后来符号代数的功效，这种传统方法甚至在乘以、除以未知数的幂等方面还明显优于后来的符号代数方法。其中蕴含的创造精神和深刻思想，可以为今天的数学研究提供借鉴。

6 中国古代位置示数法的现代价值

中国社会在清末民初发生剧变，出现所谓 “三千年未有之大变局”，整个知识体系发生从传统向现代的转型，数学也是如此。从知识体系和表达方式上看，中国现代的数学在总体上是引进的，但这并不意味着中国传统数学在现代消失了，它实际上是已融入到现代的数学体系中。比如十进位值制、九九、四则运算、比和比例、盈不足术、开方、面积和体积计算方法等。这些数学知识已成为今天人们工作和生活中一些基本的知识和观念，只是由于表达形式上的差异、数学教学中鲜有讲述其来源等原因，造成今人对中国古代数学的疏离感，所以现代人就很少知道其源于中国传统数学。因此，我们建议，在今天的教科书和教辅材料中，在教师的教学工作中，要把这些数学知识和数学方法的中国古代来源讲述清楚，并指出包括位置示数法在内的一些中国古代数学的方法和思想在某些方面的先进性。这既是对历史事实和古代先贤的尊重，也有助于激励年轻学子的文化自信，避免数典忘祖之憾。

中国传统数学内容丰富多彩，其中有些方法和思想，由于年代久远和中国学术从传统向现代的转型而湮没不彰。这种情况并不都是优胜劣汰的结果。历史的淘汰有其复杂性，中国传统数学的历史也是如此。比如，被称赞为 “精妙” 的祖冲之《缀术》在宋代失传，而宋元时代的重要成就天元术、四元术等也在明代没有得到继承，都是水平高却被淘汰的例证。这些先进数学知识失传的原因是多方面，其中一个原因反而是它们超越同时代绝大多数人的水平。既然被淘汰的不一定是落后的，那么如果我们仔细考察中国古代数学的思想和方法，就可以从中发现和汲取先进的营养，为今所用。在这一方面，吴文俊先生已经做出了表率。

1974 年春，在特殊的历史条件下，吴文俊开始学习中国古代数学史。经过两年多时间的研习，他形成了自己关于中国古代数学特征的认识。他认为，“中国古代数学基本上是一种机械化的数学”。中国古代算法不仅具有程序化、机械化和构造性特征，而且具有重视列方程、解方程的传统，并形成了系统的方法和理论，同时也发展出了几何代数化的思想方法，吴文俊对此有深刻的认识，从而大大启发了他在机器证明数学定理方面的研究。从 1976 底至 1977 年初，吴文俊在机器证明定理方面取得重大突破，之后又进一步开创了数学机械化领域的新局面。他的机器证明研究采用不同于西方流行的数理逻辑方法，而是通过建立坐标系，将几何问题代数化，通过方程和多项式理论来解决问题。他说：“我们从事机械化定理证明工作获得成果之前，对泰斯基的已有工作并无接触，更没有想到希尔伯特的《几何基础》会与机械化有任何关系。我们是在中国古代数学的启发之下提出问题并想出解决办法来的。” 他声明自己 “关于数学机械化的研究工作，就是在这些思想与成就启发之下的产物，它是我国自《九章算术》以迄宋元时期数学的直接继承”。[14]

上述吴文俊在数学史研究基础上所做的数学机械化研究，说明中国古代数学对现代数学也能提供思想和方法上的借鉴和启迪。

中国古代数学充分发挥位置的功能，不仅将它用于位值制记数法，而且用它表示未知数及其幂，甚至通过移动个别文字卡片来实现一组运算。特别是四元术，还利用各个方向的不同位置来表示各种的算式。不过，摆放算筹在水平面上只能利用前、后、左、右四个方向标示四个未知量，而在竖直面上摆放算筹就会由于重力的作用难以实现，因此超过四元的筹算操作法有着天然的难度。尽管如此，中国传统数学中利用多维度上的位置与算筹记数法以及个别的文字卡片相结合，来达到后来运用代数表达式、进行代数运算之效果的方法，展现了具有明显不同于现代符号代数的中国特征和某些优势。认真分析这种方法的原理和特征或许可以为现代数学提供启示。

由于技术条件的限制，中国古代筹算只能利用水平的二维操作面，从而使位置示数法局限于四个未知数之内。现代计算机技术的高度发展，可以模拟三维的空间结构，甚至能够可视化多维的空间结构。将这种技术结合到中国古代的四元术上，可以很快地将四元拓展到更多元的情形。如果再加以扩展，将中国传统数学中充分发挥位置作用的思想和方法与现代计算机技术结合起来，或许有可能为现代数学的发展提供新的思路。比如，采用现代的符号表示法与位置示数法表示各种算式，同时将算式置于不同的空间位置表示不同的含义，再根据问题类型的不同性质和条件，设计不同位置上的算式之间的运算法则，从而在发挥位置功能的同时，既能突破四元术由于所利用的维数少而导致未知量个数上的限制，又能充分保留现代符号代数的既有优点。这样，古老的数学操作方法，可以转化为现代数学的有效方法，从而为数学研究提供新的发展途径。当然，这只是一种可能的思路，是不是可行，怎么样才可行，皆有待今后的探索和验证。可以肯定的是，具体的应用无疑会存在意想不到的困难，还有待多方努力探索。

中国古代数学内容丰富，思想和方法多样，本文只是对其中位置示数法的特征做一简明的阐述，并对其现代意义做初步的探索。更全面的讨论，尚需俟诸异日。

致谢中国科学院数学与系统科学研究院魏蕾博士帮助查找资料，谨致谢忱。

注释

本文系中国科学院战略研究专项、中国科学院自然科学史研究所 “十四・五” 规划重大项目 “中国科技传统及其现实意义研究”（编号：GHJ-ZLZX-2021-17-2）的阶段研究成果。
钱宝琮很早就比较系统地提出位置在中国古代数学中的作用，认为中国自古以来记数法就遵从十进位制，用分离系数法表示开方式和方程，是中国古代数学的特征 [2]。其论述具有重要意义，但不是从代数符号发展的视角论述的，而且有些地方也不太准确。
已有学者注意提出中国宋元时期的 “天元术”、“四元术” 在向 “符号化” 方面 “迈出了重要一步”[3]，就功能的相似性而言是可以这样讲的，但这种说法容易忽视中国古代数学方法的特色。因为宋元数学家虽然有 “立天元一为什么”、“立地元一为什么” 等说法相当于现代 “设 $x$ 为什么”、“设 $y$ 为什么”，但在算式中 “天”、“地” 等汉字往往并不出现，而是通过位置来表现它们及其幂，相应的运算方法也有很大不同。

参考文献

[1] 李文林. 数学史教程（第三版）[M]. 北京：高等教育出版社，2011：127-131.

[2] 钱宝琮. 中国数学史话[M]. 北京: 中国青年出版社，1957: 14-18, 147-150.

[3] 李文林. 中国古代数学的发展及其影响[J]. 中国科学院院刊，2005, 20 (1): 31-36.

[4] 李俨. 筹算制度考[J]. 燕京学报, 1929(6): 1129-1144.

[5] 钱宝琮主编. 中国数学史[M]. 北京: 科学出版社, 1982: 7-9, 51-54, 168-173, 179-186.

[6] 邹大海. 中国数学的兴起与先秦数学[M]. 石家庄: 河北科学技术出版社, 2001: 95-102.

[7] 邹大海. 中国数学在奠基时期的形态、创造与发展[M]. 广州: 广东人民出版社, 2022: 84-93, 102-105, 129-137, 353-357.

[8] Zou Dahai. Whole Number in Ancient Chinese Civilisation：A Survey Based on the System of Counting-units and Expressions[J]. ICMI Study 23: Primary Mathematics Study on Whole Numbers：Proceedings (Edited by Xuhua Sun, Berinderjeet Kaur, Jarmila Novotná), Macao: International Commission in Mathematical Instruction, University of Macau, the Education and Youth Affairs Bureau, Macau SAR, 2015: 157-164.

[9] 郭书春. 九章筭术新校[M]. 合肥: 中国科学技术大学出版社, 2014: 327-328.

[10] Peter Gabriel. Matrizen, Geometrie, Lineare Algebra[M]. Basel; Boston; Berlin: Birkäuser, 1996: 19.

[11] 邹大海. 从出土简牍文献看中国早期的正负数概念[J]. 考古学报, 2010 (4): 481-504.

[12] 莫若. 四元玉鉴前序.郭书春主编. 中国科学技术典籍通汇•数学卷一[M]. 郑州: 河南教育出版社, 1993: 1205.

[13] 祖颐. 四元玉鉴后序. 郭书春主编. 中国科学技术典籍通汇•数学卷一[M]. 郑州: 河南教育出版社, 1993: 1206.

[14] 吴文俊. 吴文俊论数学机械化[M]. 济南: 山东教育出版社, 1996: 491, 430-439, 364-365.

【说明】本文刊于《数学通报》2024 年第 12 期第 51 - 56 页，题为《位置示数法：一种具有代数符号功能的中国传统数学方法》。
文章原本题为《位置示数法：一种有代数符号功能并具优势的中国传统数学方法》，虽嫌稍长，但更能反映本文主旨，故网络版恢复原标题。文章本来备有摘要，但《数学通报》不需要，现将摘要作为导读置于正文之前。