前言
我在之前的文章中提到过多次,长沙具身团队是我司建设的第二支具身团队,通过5月份的全力招聘,为了冲刺6月底和7月初来长沙办公室考察的第一批客户,过去一个多月来,长沙分部(一开始就5人,另外5人 + 实习生后面才逐个逐个进来的) 高速发展
| 机械臂(6月份侧重的机械臂) | 人形(7月份则将侧重人形) | |
| 陆续到位一系列设备 | 25年6.4日,正值我司注册十周年,在没动南京那边机器的情况下,到位了piper机械臂和宇树G1 edu 之后的6.6日,再到齐VR和吊架 | |
| 先后完成各种方式遥操机械臂 | 6.8日,在新同事们分的其中一个两人小组上,VR已可遥操piper 6.9-6.13,长沙具身团队先后完成通过键盘、手柄、VR、主从臂遥操piper机械臂的工作 | |
| 机械臂之外,开干人形 | 6.16,人形的所有配套硬件 基本全部补齐,比如vr外的:双目及深度相机 + 3d打印件,开始正式开发g1 edu 6.18 我司「七月在线」长沙分部那边,以同事朝阳为主力,我打杂,折腾了整整一天,终于可以通过VR摇操宇树G1了——当然,摇操是为了做训练数据的采集,从而方便 下一步的模型(策略)训练,最终实现机器人自主做各种任务 | |
| 机械臂上 开始陆续一系列科研复现成功 | 6.23,长沙分部新同事们完成其中一个练手项目,lerobot ACT自主抓个杯子 6.24,长沙分部几个新同事的完成又一个练手项目:抓零食 6.25,开始挑战一个难点的任务,先采数据 训练模型 最后:自主抓耳机线 插主机的耳机孔 | |
| 人形上 也开始出成果了 | 6.26日晚上,我们搞定了让机器人跳舞,且在我司长沙办公室现场让宇树G1跳查尔斯顿舞 且第二天,25年6.27上午,我们再次在长沙办公室给某车企客户演示了这个查尔斯顿舞 | |
| 机械臂上挑战难度更大、精度更高的任务 | 6.29,历时一周多,我们(同事文弱为主)通过基于uc伯克利的RL项目hil-serl,成功实现在仿真中抓方块(成功率基本100%),respect kewang 6.30,我司长沙分部挑战并完成了难度更高的任务——耳机线插耳机孔(这个任务是我们自己想出来的),成了,自主模式下,无任何摇操 7.4,通过单纯模仿学习且不加触觉情况下,使得耳机插孔的成功率达到了80% 7.11,上个月机械臂上的任务,都是用的lerobot那套框架(包含ACT和pi0),本周(7.7-7.11)完成了官方openpi在臂上的部署(训练+推理),练手一个简单任务:抓零食 相当于因为团队以前经验的积累,加上有朋友的帮助 3天完成openpi在国产臂上的部署 + 数采,2天完成训练、推理 7.12,昨天通过openpi抓零食,今天又训了一个任务,openpi自主做智能分拣 即便被分拣物体被交换了位置,也能成功分拣,毕竟vla还是比单纯il更智能些 | 人形上 7.12,除了机械臂上的各种操作外,人形也一直在做各种二次开发,比如这两天在宇树sdk基础上,做了下大模型对话功能 |
本文解读UC伯克利最近新提出来的一个工作

- 其对应的项目地址为:colinqiyangli.github.io/qc
其GitHub地址为:github.com/colinqiyangli/qc - 其paper地址为:https://arxiv.org/abs/2507.07969
一作是UC伯克利的博士生,二作也是UC伯克利的博士生且同时是PI的实习生,三作则是UC伯克利的副教授,且同时是PI的联创
PS,白天,我粗略统计了一下
- 过去一年(24年7月-25年7月),看的具身相关的论文大概是186篇,当然,不是每一篇都做了精读,值得精读的,大部分也在博客中解读了
- 当一个方向读了两三百篇论文之后,这个方向而言,便没有大的秘密了,但 还有很多小秘密
所以还得不断的读,且和团队不断的落地实践,也期待与更多具身同仁、同行多多合作
第一部分
1.1 引言、相关工作、研究背景
1.1.1 引言
如原论文所说,强化学习(RL)承诺仅依赖奖励函数即可解决任何指定任务。然而,这种简单直接的RL问题表述在实际应用中常常不可行:在复杂环境中,完全从零开始探索以学习有效策略的代价极高,因为这要求智能体在学习到良好策略之前,必须通过随机尝试偶然成功地完成任务
事实上,即使是人类和动物也很少完全从零开始解决新任务,而是利用以往经验中获得的先验知识和技能
- 受此启发,近期有大量研究致力于将先前的离线数据整合进在线RL探索过程中[27,38,82]。
说白了,因为奖励函数不好设计且泛化有挑战,故有了offline to online RL,简称O2O RL
O2O RL 的核心思想是:首先利用一个大型的、预先收集好的离线数据集(比如人类操作的机器人演示、其他策略的运行记录)进行预训练,然后在此基础上,通过与环境的少量在线交互进行微调和提升。这就像一个学徒,先看师傅的教学视频(离线数据),再亲自动手实践(在线交互)
但这又带来了一系列新挑战:离线数据的分布可能与智能体在线上应遵循的策略分布不一致,从而引入分布偏移,并且如何有效利用离线数据以获得良好的在线探索策略也并不显而易见
解决办法之一,是如此前解读过的热启动RL,即《WSRL——热启动的RL如何20分钟内控制机器人:先离线RL预训练,之后离线策略热身(模拟离线数据保留),最后丢弃离线数据做在线RL微调》
解决办法之二,是本文要介绍的Q-chunking
- 在相邻的模仿学习(IL)领域,近年来一种广泛使用的方法是采用动作分块(action chunking)
与根据先前数据中的状态观测训练策略预测单一动作不同,该方法是训练策略预测一小段未来动作序列(即“动作块”)[87,11]
举个例子:
传统模仿学习:你告诉机器人「把手抬高一点」
机器人预测并执行一个抬手的原子动作
模仿学习与动作块:你告诉机器人「拿起桌上的杯子」
机器人可能一次性预测一个包含「伸出手臂 -> 张开手掌 -> 握住杯子 -> 抬起手臂」的动作序列,然后逐一执行
虽然动作分块在IL中有效性的完整解释仍然是一个未解之谜,但其有效性至少可以部分归因于它能更好地处理离线数据中的非马尔可夫行为
——————
什么是非马尔可夫行为?简单地说,就是当前动作的选择,不仅取决于当前的状态,还可能依赖于过去一系列动作所形成的「上下文」或「习惯」,比如在模仿学习中,人类的每一次示范并不是完美的。人们在日常操作中可能存在犹豫、等待等,比如把电池插进遥控器,有点对不准,手会顿一下
本质上为建模(例如)人类演示或不同行为混合等复杂分布提供了更强大的工具[87]
动作分块在强化学习(RL)中尚未被广泛采用,可能是因为在RL的背景之下,完全可观测的马尔可夫决策过程(MDP)中的最优策略是马尔可夫性的[72],因此分块可能显得没有必要
说白了,即理论上强化学习的最终策略只需看当前状态就能做出最优决策(这叫“马尔可夫性”),不存在模仿学习中的非马尔科夫行为
- 但作者注意到,虽然一般可能希望最终获得一个最优的马尔可夫策略,但探索问题可以通过非马尔可夫性和时间扩展的技能更好地解决
而动作分块为实现这一目标提供了一种非常简单且方便的方法
换言之,虽然最终的最优策略在完全观测的 MDP 中是马尔可夫的,但探索问题可以更好地通过非马尔可夫的、时间扩展的「技能」来解决 - 此外,动作分块还为利用离线数据提供了更优的途径(能够更好地处理数据中的非马尔可夫行为),并且通过实现无偏的n步回溯『即enabling unbiased n-step backups,其中n等于分块长度』,甚至提升了基于TD的强化学习的稳定性和效率
在强化学习中,一个关键环节是“回头看”之前的决策好不好,也就是价值回溯
chunking 通过“动作分块”的方式,一次性预测和评估多步连续动作,让系统能整体判断一段行为的价值,不仅回溯更快,还能避免传统多步方法中常见的估值偏差
因此,结合对离线数据的预训练,动作分块为缓解强化学习中的探索难题提供了一种极具吸引力且非常简单的方式
对此,来自UC伯克利的研究者提出了带有动作分块的Q学习(简称Q-chunking),这是一种在离线到在线强化学习(RL)环境中改进通用时序差分(TD)型actor-critic RL算法的方法『即a recipe for improving genericTD-based actor-critic RL algorithms in the offline-to-online RL setting』
详见见下图图1
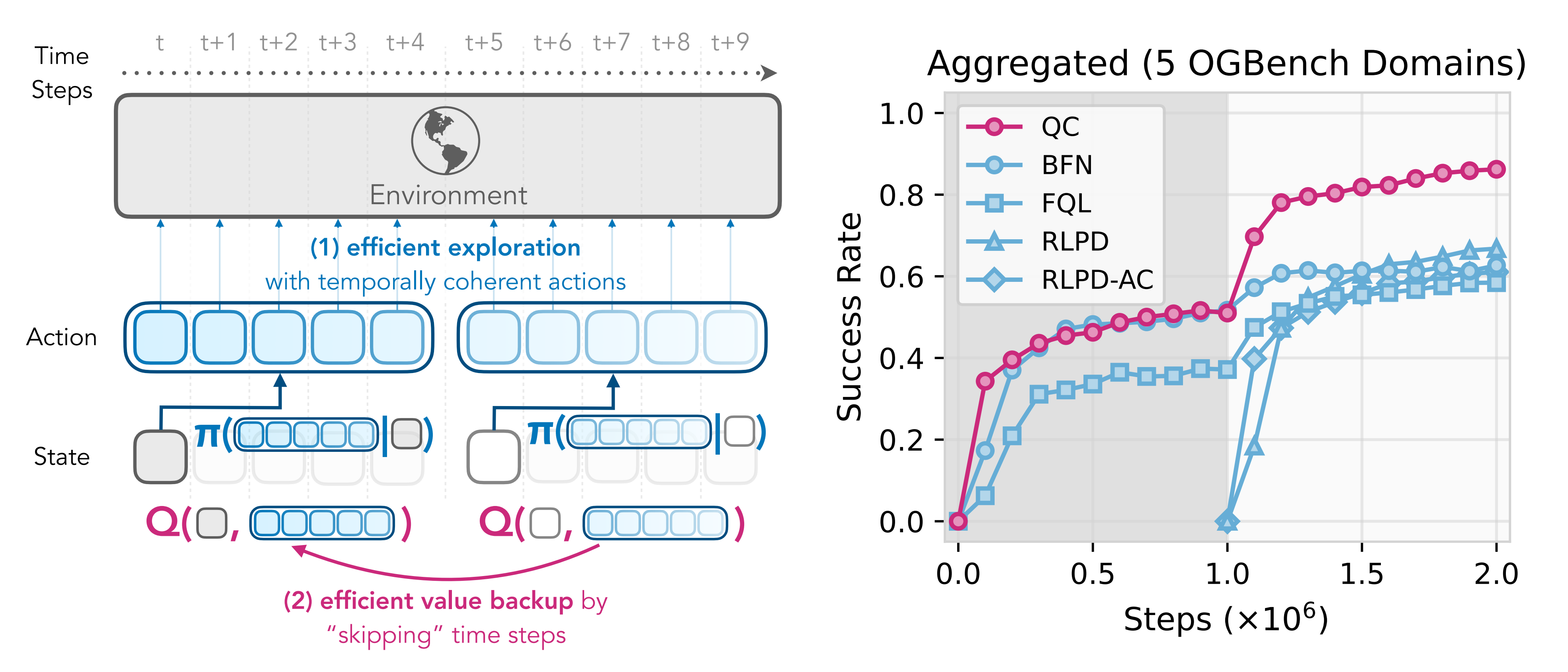
其核心思想是在动作序列层面运行强化学习
- 策略预测未来h步的动作序列,并以开环方式逐步执行这些动作
- 评估器(critic)接收当前状态和一个动作序列,并估算执行整个动作序列的价值,而不是单独的某个动作
在这个扩展动作空间上运行强化学习有两个主要好处:
1 通过将策略正则化到表现出时间连贯性的先验行为数据上,可以优化策略以生成时序一致的动作
2 用标准TD回传损失训练的评估器实际上是在执行n步回传,并且没有通常出现在朴素n步回报方法中的离策略偏差,因为评估器考虑了完整的动作序列
1.1.2 相关工作
第一,对于离线到在线强化学习方法
侧重于利用先前的离线数据来加速在线强化学习[85,69,36,1,86,88,7,49,89,38]
- 最简单的离线到在线强化学习方法是,首先使用现有的离线强化学习算法在离线数据上进行预训练,然后继续采用相同的离线优化目标,在不断扩展的数据集上进行在线训练,结合了原始离线数据和重放缓冲区数据 [48,35,32,74,56,2,41,36]
虽然这种朴素的方法实现简单,但通常会导致过于悲观的估计,从而抑制探索,进而影响在线采样效率。已有多项研究尝试通过在线调整悲观程度来解决这一问题 [89,49,41,36,79] - 然而,这些方法往往难以调优,并且在在线采样效率方面,有时仍不及一个简单且正则化良好的在线强化学习算法,即从头开始同时学习离线数据和在线重放缓冲区数据 [7-Efficient online reinforcementlearning with offline data]
Q-chunking的方法通过价值回传加速和时间一致性的探索,进一步提升了离线到在线强化学习方法的样本效率
第二,对于动作分块(action chunking)
其是一种由机器人学家在模仿学习(IL)领域推广的技术,该方法让策略以开环方式预测并执行一系列动作(即“动作块”)[82]
- 研究表明,动作分块能够提升策略的鲁棒性[87,22,8],并能处理离线数据中的非马尔可夫行为[87]
现有结合动作分块的强化学习(RL)方法通常侧重于对通过模仿学习预训练的策略进行微调[59]——即有的先模仿学习做预训练,然后RL做微调 - Tian等人[75]提出,通过将n步回报与Transformer结合,学习基于动作块的评价器(critic)。然而,他们的方法仅将分块应用于评价器,而仍然优化单步行动者(actor)
Li等人[37]同样观察到,在短动作块上学习评价器可以消除n步回报备份中的离策略偏差,从而实现更稳定和高效的价值学习
不过该的工作与Q-chunking的工作存在关键差异——Li等人[37]在在线分幕RL场景下进行操作[81,30],并采用高斯策略预测运动基元(Motion Primitives, MP)[61,52]的参数,这些参数随后在每个回合开始时用于生成完整的动作序列
传统的RL中,策略通常被建模为高斯分布,即在给定状态下,动作服从某个均值和方差的高斯分布。这种简单模型难以捕捉离线数据中复杂的、多模态的、非马尔可夫的行为模式
所以,也就有了如果仅仅将动作块引入传统的 RLPD 算法,但策略仍使用高斯分布(RLPD-AC),但如图2所示,作者发现高斯策略效果不佳,比如其性能远低于不使用动作块的原始 RLPD
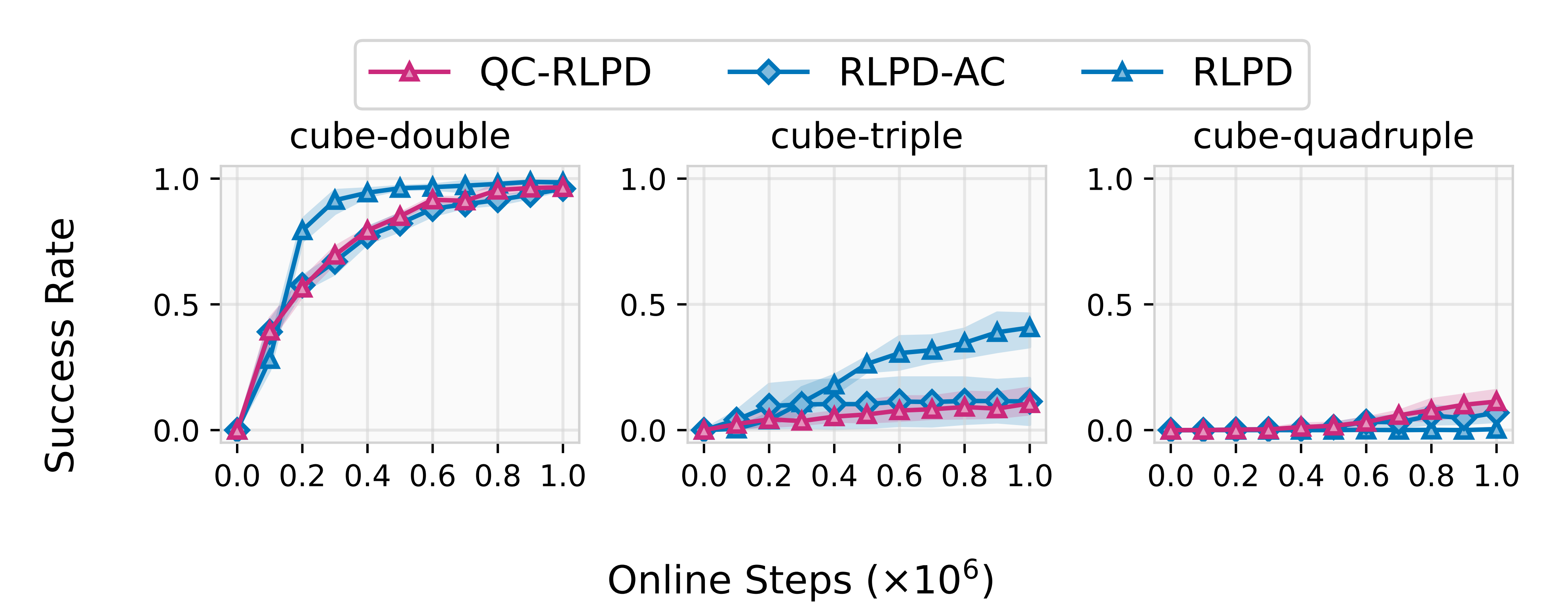
(1) RLPD在离线数据和在线回放缓冲区上运行在线强化学习 [7]
(2) RLPD-AC与RLPD为同一算法,但在时间扩展的动作空间中运行(动作块大小为5)
(3) QC-RLPD在actor上额外采用行为克隆损失(4个种子)
相比之下,Q-chunking在传统的离线到在线RL设置中工作,并利用更具表达能力的基于流匹配(flow-matching)的策略,直接在原始动作空间中预测短动作序列
下文1.2.3 节会详解 - Seo和Abbeel[63]同样在动作块上训练评价器,并施加行为克隆损失,这与Q-chunking背后的原理一致
与Q-chunking的工作的关键区别在于,他们采用了多层次、因式分解的评价器架构[64],通过迭代离散化从粗到细生成并细化动作块
在每一层,动作空间被离散化为若干区间,Q函数针对每个动作维度和时间步独立建模,条件为上一粗层级预测的整个动作块
虽然这种因式分解的评价器设计使得价值最大化的动作采样变得可行,但它对动作空间施加了较强的结构性假设,限制了每个细化层级的策略表达能力
相比之下,Q-chunking的方法不做此类假设,使得能够推导出两种通用算法,其中评价器和策略均可直接作用于动作块,无需因式分解或迭代离散化/细化
第三,对于采用时序一致的动作进行探索
- 现有方法
要么依赖于通过启发式构建的时序相关动作噪声[39]
要么采用分层结构的策略(详见下文)
但这种方法在在线训练过程中往往难以稳定
或者使用预训练且冻结的技能策略[58,82],这类方法不便于进行细粒度的在线微调 - 本文的方法使用单一网络来表示策略,生成具有时序延展性的动作片段,并通过一个易于优化且稳定的目标函数进行训练
此外,Q-chunking的方法不包含任何冻结或预训练的组件,从而保证了在线微调的灵活性
第四,分层强化学习与选项框架
关于学习时间延展动作的研究也在分层强化学习(HRL)文献中得到了广泛关注[14,16,77,13,34,78,57,60,47,3,65,58,21,84]
- HRL方法通常训练一组能够直接与环境交互的低层策略,并配合一个高层策略来选择这些低层策略。低层策略可以是手工设计的[12],也可以通过在线方式自动发现[16,34,77,78,47],或者利用离线技能发现方法进行预训练[52,45,65,3,68,58,76,50,27,19,9,55]
- 选项框架则提供了一种更为复杂且功能更强大的形式化方法,其中低层策略还与可学习的启动条件和终止条件相关联,使低层策略的使用更加灵活[73,44,10,43,66,67,31,13,70,51,18,4,29,5,6,15]
- HRL领域长期存在的挑战在于其双层优化问题:在训练过程中同时更新低层和高层策略时,高层策略必须针对不断变化的目标函数进行优化,这可能导致不稳定性[47]
为了解决这一问题,一些方法会在初步预训练后冻结低层策略[3,58,82],以提升在线训练过程中的稳定性
本文的方法是HRL的一个特例,其中低层技能以开环方式执行一系列动作。这一设计选择使得作者能够将双层优化问题简化为在时间延展动作空间中的标准强化学习目标,同时保留了许多HRL方法相关的探索优势
第五,多步潜在空间规划与搜索
- 这是一种常见于基于模型的强化学习方法的技术,这些方法利用学习得到的模型来优化短期动作序列,以获得高回报的轨迹 [51,62]。这些方法通过在编码后的潜在空间上训练动力学模型实现,其中模型接收一个潜在状态和一个动作,预测下一个潜在状态及其对应的奖励值。
该潜在动力学模型与潜在状态上的价值网络结合后,能够通过在潜在动力学模型中简单地模拟动作序列,为任意给定的潜在状态出发的动作序列即时提供 Q 值的估计 - 相比之下,Q-chunking并不学习潜在动力学模型,而是直接训练一个 Q 网络来估算动作序列的价值
最后,这些方法主要应用于纯在线强化学习场景,而Q-chunking则关注从离线到在线的强化学习设定
1.1.3 研究背景:离线到在线RL、时序差分与多步回报
首先,对于离线到在线强化学习
在本文中,作者考虑一个无限时域、完全可观测的马尔可夫决策过程(MDP)
其中
是状态空间
是动作空间
是转移核
是奖励函数
是初始状态分布
是折扣因子
- 且还假设存在一个先验的离线数据集D 由来自
的转移轨迹
组成
离线到在线强化学习的目标是找到一个策略,使得期望折扣累计奖励(或折扣回报)最大化:
如上文提到过的,离线到在线强化学习算法分为两个不同的阶段:
- 离线阶段,在离线数据D 上对策略进行预训练
- 在线阶段,通过与环境的交互进一步微调策略
其次,对于时序差分与多步回报
基于时序差分(TD)的强化学习算法通常通过使用时序差分(TD)损失函数[72],学习,以近似从状态 s 和动作 a 出发时,策略能够获得的最大期望折扣累计回报:
其中,是对
的估计,通常选择为
:
其中,是从某些离策略轨迹中采样的,
是
的一个延迟版本,为了学习的稳定性,不允许梯度通过
- 当TD 误差被最小化时,
收敛到策略
的期望折扣值
随着有效视野的增加,学习速度变慢,因为价值只向后传播一步(从
到
)
- 为了加速长视野的价值回传,一个常见的策略是采样长度为
的轨迹片段
,并由此构造一个
步回报[80,72]——定义为公式3
其中,
该的价值估计允许价值在时间步数上传播时实现
倍的加速。该估计器有时被称为未修正的
步回报估计器[17,33],因为当数据收集策略与当前策略
不同时会产生偏差
尽管如此,由于n 步回报实现简单,它已被广泛应用于大规模RL 系统[46,25,28,83]
1.2 Q-Chunking(Q-分块)的完整方法论
如原论文所述,接下来,会首先介绍Q-分块的两个主要设计原则:
- 在时间扩展的动作空间(即动作块的空间)上进行Q学习
- 在该扩展动作空间中施加行为约束
随后,将介绍Q-分块(QC,QC-FQL)的实际实现方法,这些方法作为有效的基于时序差分(TD)的离线到在线强化学习算法『followed by practical implementations of Q-chunking (QC, QC-FQL) as effective TD-based offline-to-online RL algorithms』
1.2.1 在动作块空间上的Q-Learning:加速价值传播且可无偏估计
传统强化学习中的 Q 函数评估的是在状态
下执行单个动作
所能获得的最大未来折扣奖励,而Q-chunking的首要设计原则是在时间扩展的动作空间(即动作块空间)上应用Q学习
与普通的基于一步时序差分(TD)的actor-critic方法不同,后者(一步时序差分TD)训练的是Q函数和策略
而Q-chunking的方法则用一连串的 h 个连续动作来同时训练critic 和actor
即we instead train both the critic and the actor with a span of h consecutive actions
在实际操作中,这包括对批量的转移数据进行评论者(critic)和行动者(actor)的更新,这些转移数据由一个随机状态
、一个后续动作序列以及状态
和未来第
步的状态
组成
具体而言,作者通过以下时序差分(TD)损失函数来训练
其中,且
是目标网络参数,通常是
的指数移动平均值 [24]
上述 TD 损失与公式 3
中的 n 步回报具有显著相似性(其中 n 等于 h)
但存在一个关键区别:n 步回报备份中使用的 Q 函数仅接收一个动作(在时间步t),而Q-chunking的 Q 函数则接收整个动作序列
这个区别的意义可以通过分别写出标准 1 步 TD、n 步回报和 Q-chunking 的 TD 备份方程来更好地解释
- 对于标准的1步时序差分(TD)方法,每次回传仅将价值向前传播一步
它将当前状态 - 动作对的 Q 值更新为即时奖励加上下一状态 - 动作对的折扣 Q 值。每次更新,价值信息只回溯一步。对于长周期任务,这意味着价值信号需要很长时间才能从最终奖励传播回来,学习速度很慢
- n步回报(n-step return),可以将价值以
倍的速度向前传播,相当于将
时刻的 Q 值更新为:未来
步的实际奖励总和,加上第
步后的折扣 Q 值。这样,每次更新能将价值信息回溯
步,理论上能加速学习
但当区间和
为离策略(off-policy)时,可能会出现有偏的价值估计问题[17],这是因为数据集或回放缓冲区中
步奖励
的折扣和,不再是当前策略
下期望
步奖励的无偏估计
啥意思呢,这里存在一个关键问题:偏差(Bias)
如果用于计算 TD 目标的数据(从离线数据集或回放缓冲区中采样)是由一个行为策略
生成的,而当前学习的策略是
那么前
步的实际奖励
——从 行为策略 πβ 的数据 中采样的,并不能无偏地代表当前策略
会获得的
步奖励
因为在这
步内可能采取与
不同的动作,从而导致不同的奖励序列。这种偏差在离线RL中尤为突出
上面说了一大堆,但如果对于刚学RL的初学者来说,绕老绕去绕晕了,so,到底啥意思呢,我还是用生活中的例子来做个类比
假设你是一个学生(学习策略
),正在复习历史考试。你手里有一份别人(行为策略πβ)整理的错题笔记(离线数据集)
- 这份笔记记录了别人做题时的每一步选择(动作 a)和对应的得分(奖励 r)
现在你想通过这份笔记快速学会“如何得高分”
n 步回报的策略是:
“我不仅看当前这一步的得分,还连续看接下来 n 步的得分,来总结规律。”- 但问题是:
别人(πβ)的解题思路可能和你()完全不同
比如别人在某一步选了“背朝代口诀”——πβ的动作,而你更倾向于“理解历史背景”(的动作)
如果盲目用别人的后续得分来指导你,可能会误导你——因为你们的选择不同,后续的得分路径也会不同。这就是偏差(Bias)的来源:
用别人的行为数据(πβ)来估算你自己的策略(π)的价值,会导致价值估计不准确
- Q-chunking价值回传与
步回报类似,每步也将价值向前传播h步,但不会出现这种有偏估计问题
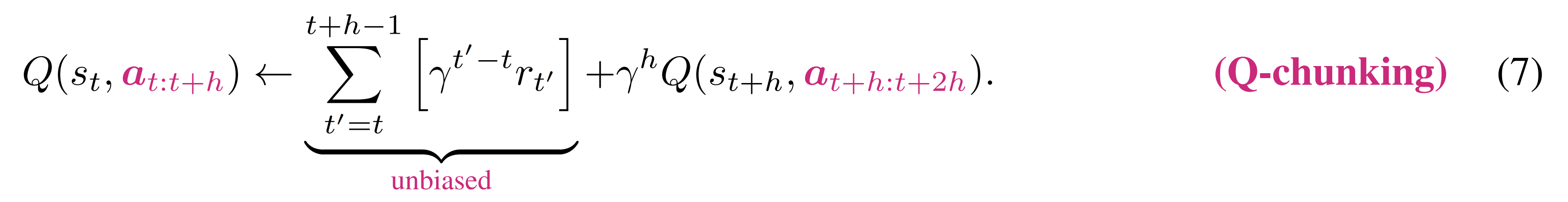
原因在于与步回报将价值回传到1步Q函数不同,Q-chunking回传将价值回传到
步Q函数,该函数接收与获得
步奖励
时完全相同的动作,从而消除了有偏价值估计
因此,Q-chunking价值回传在加速价值传播的同时,能够保持无偏的价值估计
说白了,Q函数
的输入就是整个动作块
,而TD目标中的奖励求和项
,正是执行这个动作块
所获得的实际奖励
为什么这能消除偏差?
- 因为 Q 函数评估的就是「在
状态下,如果执行了
这个特定序列,能得到多少价值?」
- 右边的奖励项
,也正是这个特定序列所产生的实际奖励
这就好比,你问「如果我按照这个菜谱做菜,会得到什么味道?」,然后你实际按照菜谱做了,尝到了味道。这个味道就是无偏的,因为它就是「这个菜谱」的结果
1.2.2 时序一致性探索的行为约束:解决动作不一致(利用离线数据中具有时序连贯性的动作序列)
Q-chunking 的第二个设计原则通过在 的目标中引入行为约束,解决了动作不一致性问题——定义为公式8:
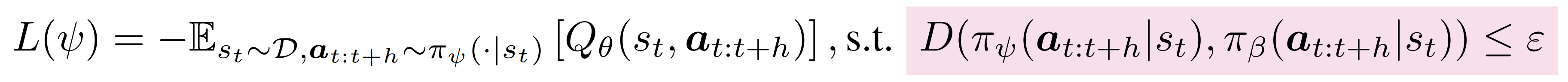
其中,将表示为离线数据
中的行为分布,
表示某种距离度量,用于衡量学习到的策略
与
偏离程度
直观来看,对时序扩展动作序列施加行为约束,使得能够利用离线数据集中具有时序连贯性的动作序列
- 这在时序扩展动作空间中尤其具有优势,相较于原始动作空间,因为离线数据通常呈现非马尔可夫结构『例如,来自脚本化策略[54]、人工远程操作员[42]或用于子任务的噪声专家策略[54,20]』,而这些结构无法被马尔可夫行为约束很好地捕捉
时序连贯的动作对于在线探索来说是理想的,因为它们类似于时序扩展的技能(如在导航中朝某一方向移动、越障动作等),有助于以结构化的方式穿越环境,而不是使用随机动作——随机动作往往导致数据局限于初始状态附近
说白了,离线数据,特别是人类演示,天然就包含这种时间连贯的、有目的性的行为。例如,人类操作机器人时,不会随意地移动一个关节,而是会执行「伸手」、「抓取」、「移动」等一系列结构化的动作。Q-chunking 的目标就是利用这些「人类智慧」来指导智能体的在线探索 - 对动作分块策略施加行为约束,是一种非常简单的方法,可以近似地提取技能,而无需像基于技能的方法那样训练具有双层结构的策略
实际上,作者确实观察到,带有此类行为约束的Q分块能够通过时序一致性的动作与环境交互和探索,从而缓解了强化学习中的探索难题
1.2.3 实际实现:QC与QC-FQL
Q-chunking 的一个关键实现难点在于,如何在动作序列层面施加能够体现非马尔可夫行为的良好行为约束。实施良好行为约束的前提之一,是策略能够捕捉复杂的行为分布(例如,通过流模型/扩散策略)
- 首先,而如上文提到过的,高斯策略作为在线强化学习算法中的默认选择,并不足以满足这一需求。实际上,如果直接采用现成的在线算法(例如 RLPD[7]),并结合行为克隆损失应用 Q-chunking,通常会发现其表现较差,即如上文出现过的图2
- 其次,如此文所说,流匹配是一种生成模型,它的思想是学习一个连续的动力学过程(continuous dynamics),将一个简单的初始分布(例如标准高斯噪声)平滑地转化为任意复杂的目标数据分布
你可以把它想象成:你有一团泥巴(高斯噪声),流匹配就是学习一套「雕刻路径」,能把这团泥巴精准地雕刻成任何你想要的形状(复杂的动作块分布)
通过流匹配训练的行为策略,能够:
捕捉复杂分布:在高维动作块空间中建模多模态、非马尔可夫的复杂行为分布
生成高质量样本:从噪声中生成与离线数据中观察到的行为模式高度相似的、时间连贯的动作块
为了施加良好的行为约束,作者首先使用flow-matching 目标[40] 来训练一个行为克隆流策略,以捕捉行为分布
该流策略由一个状态条件下的速度场预测模型 参数化,作者用
表示流策略参数化的动作分布,它作为离线数据中真实行为分布的近似(
)
有了这个强大的行为策略 ,Q-chunking 提出了两种实用的实现方案,一个是QC,一个是QC-FQL
1.2.3.1 QC:即带有隐式KL行为约束的Q-chunking
简言之,QC(Q-chunking with Implicit KL Behavior Constraint) 不显式地训练一个独立的策略网络来最大化 Q 值,而是通过 Best-of-N 采样 的方法来实现策略优化和行为约束的结合
还是说的再直白点吧
- 它首先训练一个特殊的“流策略”(flow policy)来掌握离线数据中复杂的、多步骤的行为
- 然后,在在线学习时,它利用这个策略生成若干个候选的“动作块”(比如,生成 16 个)
- 接着,它用其价值函数(Q - function)从这些候选项中选出最好的一个并执行。这种“N 选最优”的采样方式,巧妙地让智能体的行为不会偏离从数据中学到的有效策略太远
如公号具身纪元所说,这个设计的目的是不希望 AI 的行为和人类演示偏差太大,但又不想“死盯着人类的动作照抄”,而是希望它“以人为参考,自主发挥”
就像你让 AI 学炒菜,给它一个人类炒菜的 10 段视频,它每次从中“学一段”,但不是照抄,而是从中挑一段看起来最香的学。这种挑选方式既靠近人类风格,又保留优化空间
具体而言,作者通过学习到的行为分布对他们的策略施加KL约束——定义为公式9:
虽然可以将KL作为损失函数的一部分,但对于流模型来说,估算KL散度或对数概率在实际操作中具有挑战性
因此,作者采用best-of-N采样方法[71],在最大化Q值的同时,整体上隐式施加KL约束
- 具体来说,这包括首先从学习到的行为策略
中——即预训练好的流匹配行为策略,采样N个动作分块
- 然后选择能够最大化时序扩展Q函数的动作块样本:
已有研究表明,最佳N采样对原始分布的KL散度存在一个闭式上界 [26]:
这在一定程度上隐式满足了KL约束(见公式9)。直接调整N的取值对应于约束强度的变化
由于作者使用best-of-N 采样来近似策略优化(公式8)
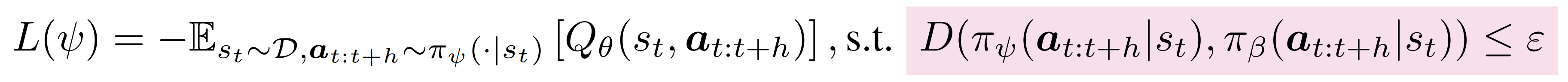
作者可以完全避免单独对策略进行参数化,只需从行为策略
中采样即可
具体来说,作者使用best-of-N采样来生成动作,用于(1)与环境交互,以及(2)在TD 回传中提供动作样本,遵循Ghasemipour 等人[23] 的方法
因此,他们的算法只需一个额外的损失函数:
其中,
虽然QC方法简单且易于实现,但确实会带来一些额外的计算开销(采样N×)。故作者又提出了该方法的一个变体,该变体利用了更为廉价的现成离线/离线到在线强化学习方法FQL[56]
1.3.1.2 QC-FQL:带有2-Wasserstein距离行为约束的Q-chunking
简言之,这是隐式 KL 约束一个计算成本稍低的变体。它不采用“N 选最优”采样,而是训练一个独立的策略网络,并通过正则化使其行为与“流策略”保持接近。这用另一种方式达到了同样的目标,即在优化奖励的同时,充分利用离线数据
如果说 QC 是“从人类动作中挑最好的”,那 QC - FQL 更像是“你自己创造动作,但每次都检查:这段动作离人类动作有多远?太远了就拉回来一点”
// 待更





MySQL学习笔记(完):事务和锁)










模式 透明装饰模式与半透明装饰模式)


复现与原理分析)