LeetCode 101. 对称二叉树 - 力扣【难度：简单；通过率：62.6%】，这道题与前一题：LeetCode100 基本相似，都是递归的思路，解法可以对照参考上一篇博文： leetcode100.相同的树（递归练习题）

一、 题目描述

给你一个二叉树的根节点 root，检查它是否是 镜像对称（轴对称） 的

示例:

示例 1:

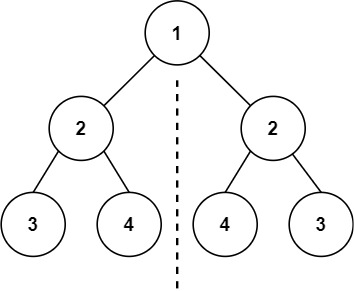
输入: root = [1,2,2,3,4,4,3]
输出: true

示例 2:

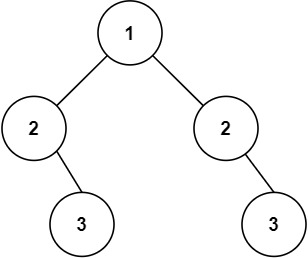
输入: root = [1,2,2,null,3,null,3]
输出: false

---

二、 核心思路：判断左右子树是否互为镜像

一棵树是否对称，其本质在于：它的左子树和右子树是否互为镜像

因此，我们可以将问题分解为：

1. 从根节点开始，判断其左子树和右子树是否互为镜像
2. 递归地，对于任意一对需要判断是否互为镜像的节点 left 和 right：
   • left 的左孩子，应该与 right 的右孩子互为镜像
   • left 的右孩子，应该与 right 的左孩子互为镜像

---

三、 递归的终止条件 (Base Cases)

在递归函数中，正确处理基准情况是关键。对于判断两个节点是否互为镜像，有以下几种情况：

• 情况一：两个节点都为空
  • 如果 left 和 right 都为 null，它们是镜像的。返回 true
• 情况二：只有一个节点为空
  • 如果 left 为 null 而 right 不为 null，或者 left 不为 null 而 right 为 null，它们不可能是镜像的。返回 false
• 情况三：两个节点都不为空，但值不同
  • 如果 left 和 right 都不为 null，但 left.val != right.val，它们的值不同，因此不互为镜像。返回 false

---

四、 代码实现与深度解析

【一种参考代码】：

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {// 主入口函数：判断整棵树是否对称，即判断其左子树和右子树是否互为镜像public boolean isSymmetric(TreeNode root) {// 如果根节点为空，根据定义，空树也是对称的if (root == null) {return true;}// 调用辅助函数，判断根节点的左右孩子是否互为镜像return isMirror(root.left, root.right);}/*** 辅助递归函数：判断两棵子树（以 left 和 right 为根）是否互为镜像* @param left  第一棵子树的根节点* @param right 第二棵子树的根节点* @return 如果两棵子树互为镜像，则返回 true；否则返回 false*/public boolean isMirror(TreeNode left, TreeNode right) {// 1. 基准情况一：两个节点都为空，它们互为镜像if (left == null && right == null) {return true;}// 2. 基准情况二：只有一个节点为空（由于是 else if，排除了都为空的情况）// 此时，一个为空，一个不为空，肯定不互为镜像else if (left == null || right == null) {return false;}// 3. 基准情况三：两个节点都不为空，但值不相等，不互为镜像else if (left.val != right.val) {return false;}// 4. 递归调用：// 如果以上基准情况都未命中（即 left 和 right 都不为空且值相等），// 则继续递归判断它们的子节点是否互为镜像// 关键点：left 的左孩子要与 right 的右孩子比较 (isMirror(left.left, right.right))//         left 的右孩子要与 right 的左孩子比较 (isMirror(left.right, right.left))// 只有这两对都互为镜像，当前这对节点才算互为镜像return isMirror(left.left, right.right) && isMirror(left.right, right.left);}
}

---

五、 关键点与复杂度分析

• 函数职责分离：isSymmetric 负责初始调用，isMirror 负责具体的递归判断。这种分离使得代码逻辑更清晰
• 对称性体现：递归调用 isMirror(left.left, right.right) 和 isMirror(left.right, right.left) 是本题的核心，它完美地体现了镜像对称的定义
• Base Case 的全面性：对三种基准情况的清晰划分，确保了递归的正确终止和各种边界条件的覆盖
• 时间复杂度：O(N) 其中 N 是二叉树的节点数。每个节点最多被访问一次（通过 isMirror 函数中的 left 或 right 参数），进行常数次比较操作
• 空间复杂度：O(H) 其中 H 是二叉树的高度。这主要是递归调用栈的空间开销。最坏情况下（树退化为链表），H 可以达到 N，所以空间复杂度为 O(N)

---

六、 总结与对比 (LC100 vs LC101)

特性	LeetCode 100 (相同的树)	LeetCode 101 (对称二叉树)
问题定义	判断两棵独立的树 p 和 q 是否结构和值都相同	判断一棵树 root 是否自身镜像对称
递归入口	isSameNode(p, q)	isMirror(root.left, root.right)
递归调用	isSameNode(p.left, q.left) 和 isSameNode(p.right, q.right)	isMirror(left.left, right.right) 和 isMirror(left.right, right.left)
核心差异	同向比较：左对左，右对右	交叉比较：左的左对右的右，左的右对右的左