1 单选题（每题 2 分，共 30 分）

第1题 已知小写字母 b 的ASCII码为98，下列C++代码的输出结果是（   ）。

1. #include <iostream>
2. using namespace std;
3. int main() {
4.     char a = 'b' ^ 4;
5.     cout << a;
6.     return 0;
7. }

A. b                                    B. bbbb                               C. f                                       D. 102

解析：答案C。'b‌'为字符型，等人价整型98，'b' ^ 4等价98 ^ 4 = 0b01100010 ^ 0b00000100 = 0b01100110 = 102。char a表示a为字符型，102将转换为字符'f'。‌‌‌‌所以C.正确。故选C。

第2题 已知 a 为 int 类型变量， p 为 int * 类型变量，下列赋值语句不符合语法的是（   ）。

A. *(p + a) = *p;                 B. *(p - a) = a;                    C. p + a = p;                           D. p = p + a;

解析：答案C。本题考察的是‌指针运算的合法性‌，关键点在于‌指针变量是否可以用于赋值表达式的左侧‌。‌A. *(p + a) = *p;‌ ‌合法‌：*(p + a) 是对指针 p 偏移 a 后的地址解引用，并赋值 *p 的值，这是合法的指针运算和赋值操作。‌B. *(p - a) = a;‌ ‌合法‌：*(p - a) 是对指针 p 偏移 -a 后的地址解引用，并赋值为 a，这也是合法的指针运算和赋值操作。‌C. p + a = p;‌ ‌非法：p + a 是一个‌临时计算的指针值(地址值)‌，不能出现在赋值语句的左侧（即不能作为左值），编译器会报错，因为表达式 p + a 的结果是‌不可修改的临时对象‌。‌D. p = p + a;‌ ‌合法‌：对指针变量 p 进行偏移运算（p + a），并将结果赋值给 p，这是合法的指针运算和赋值操作。故选C。

第3题 下列关于C++类的说法，错误的是（   ）。

A. 如需要使用基类的指针释放派生类对象，基类的析构函数应声明为虚析构函数。

B. 构造派生类对象时，只调用派生类的构造函数，不会调用基类的构造函数。

C. 基类和派生类分别实现了同一个虚函数，派生类对象仍能够调用基类的该方法。

D. 如果函数形参为基类指针，调用时可以传入派生类指针作为实参。

解析：答案B。若基类析构函数‌未声明为虚析构函数‌，通过基类指针释放派生类对象时会导致‌内存泄漏‌（仅调用基类析构函数，派生类部分未被释放），‌虚析构函数‌确保多态性析构的正确调用，所以A.正确。‌构造派生类对象时，会先调用基类构造函数，再调用派生类构造函数‌，若基类未定义默认构造函数，派生类构造时必须显式初始化基类，所以B.错误。派生类通过 base:: 显式调用基类虚函数（如 base::Method()），或通过基类指针/引用调用（覆盖后仍可访问基类实现），‌基类指针可以指向派生类对象‌（多态性），因此传入派生类指针作为基类指针的实参是合法的，所以D.正确。故选B。

第4题 下列C++代码的输出是（   ）。

1. #include <iostream>
2. using namespace std;
3. int main() {
4.     int arr[5] = {2, 4, 6, 8, 10};
5.     int * p = arr + 2;
6.     cout << p[3] << endl;
7.     return 0;
8. }

A. 6                                                                           B. 8

C. 编译出错，无法运行。                                        D. 不确定，可能发生运行时异常。

解析：答案D。arr是数组arr的首地址，即地址指向下标0，也就是元素2这个位置，int *p = arr + 2，指针p指向arr+2，即指向下标2，也就是元素6这个位置，这个位置相当于p[0]，所以p[3]已超arr的范围，结果不确定，所以D.正确。故选D。

第5题 假定只有一个根节点的树的深度为1，则一棵有N个节点的完全二叉树，则树的深度为（   ）。

A. ⌊log₂(N)⌋+1                    B. ⌊log₂(N)⌋                         C. ⌈log₂(N)⌉                              D. 不能确定

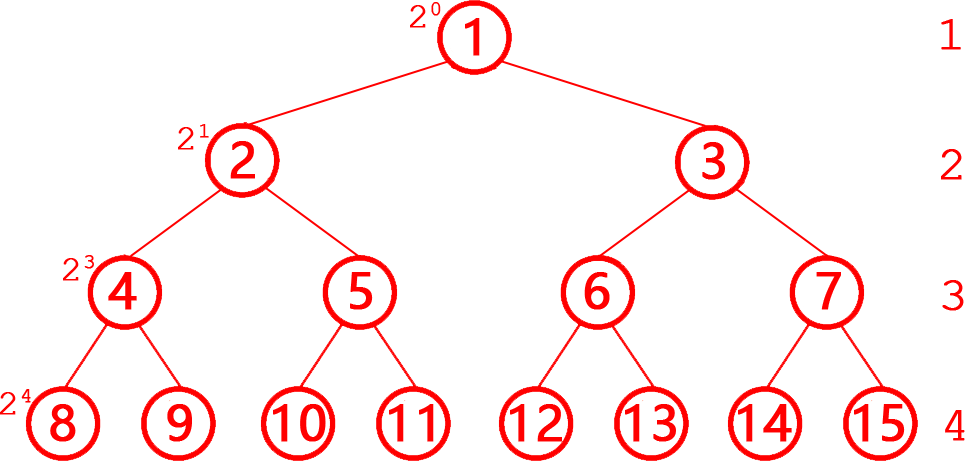
解析：答案A。完全二叉树每行的第1个节点的编号=为2层号-1，层号=log₂编号+1，对整层的其他节点：层号=⌊log₂编号⌋+1，对最后一层就是深度(参考下图)，所以对一棵有N个节点的完全二叉树，如根节点的树的深度为1，则树的深度=⌊log₂N⌋+1。故选A。

第6题 对于如下图的二叉树，说法正确的是（   ）。

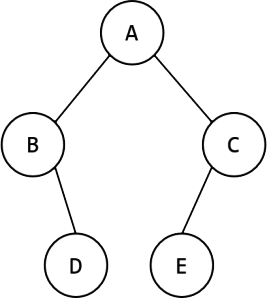
A. 先序遍历是 ABDEC 。                                         B. 中序遍历是 BDACE 。

C. 后序遍历是 DBCEA 。                                         D. 广度优先遍历是 ABCDE 。

解析：答案D。先序遍历是根-左树-右树，中序遍历是左树-根-右树，后序遍历是左树-右树-根，广度优先遍历是按层从上到下，每层从左到右。对本题图中二叉树：先序遍历是ABDCE，A.错误；中序遍历是BDAEC，B.错误；后序遍历是DBECA，C.错误，广度优先遍历是ABCDE，D.正确。故选D。

第7题 图的存储和遍历算法，下面说法错误的是（   ）。

A. 图的深度优先遍历须要借助队列来完成。

B. 图的深度优先遍历和广度优先遍历对有向图和无向图都适用。

C. 使用邻接矩阵存储一个包含𝑣个顶点的有向图，统计其边数的时间复杂度为𝑂(𝑣²)。

D. 同一个图分别使用出边邻接表和入边邻接表存储，其边结点个数相同。

解析：答案A。深度优先遍历（DFS）通常使用‌栈‌（递归或显式栈）实现，而广度优先遍历（BFS）才需要队列，所以A.错误。两种遍历算法均适用于有向图和无向图，仅访问顺序和实现细节可能不同，所以正确。包含𝑣个顶点的有向图的邻接矩阵需要遍历整个𝑣×𝑣矩阵才能统计边数，时间复杂度为 𝑂(𝑣²)，C.正确。无论出边还是入边邻接表，每条边均被存储一次，仅方向不同，边结点总数相同，D.正确。故选A。

第8题 一个连通的简单有向图，共有28条边，则该图至少有（   ）个顶点。

A. 5                                      B. 6                                       C. 7                                            D. 8

解析：答案B。对于‌连通的简单有向图‌，若共有28条边，其最少顶点数的计算逻辑如下：

‌对于简单有向图，若顶点数为𝑛，则最大边数为𝑛 (𝑛−1)（每个顶点与其他 𝑛−1 个顶点各有一条有向边）。题目要求边数28，需满足𝑛 (𝑛−1)≥28，即𝑛²−𝑛−28 ≥ 0，解方程≈5.82，因此最小的𝑛 =6。验证：当n=8时，8×7=56≥28；当n=7时，7×6=42≥28；n=6 时，6×5=30≥28；当n=5 时，5×4=20<28（不满足）。因此，‌最少需要6个顶点‌才能容纳28条边且保持连通性。‌连通性约束：连通有向图需保证至少n−1 条边（如生成树结构），但题目边数（28）远大于此下限，故顶点数由边数上限决定为6。故选B。

第9题 以下哪个方案不能合理解决或缓解哈希表冲突（   ）。

A. 在每个哈希表项处，使用不同的哈希函数再建立一个哈希表，管理该表项的冲突元素。

B. 在每个哈希表项处，建立二叉排序树，管理该表项的冲突元素。

C. 使用不同的哈希函数建立额外的哈希表，用来管理所有发生冲突的元素。

D. 覆盖发生冲突的旧元素。

解析：答案D。在每个哈希表项处，用不同哈希函数再建一个哈希表管理冲突元素，但嵌套哈希表会显著增加空间复杂度，且二次哈希函数的设计需保证不引发新的冲突，实现复杂，A.可以解决，但不算很理想。在每个哈希表项处建立二叉排序树管理冲突元素，这是链地址法的优化变种，可提高查询效率，B.可以解决。使用不同哈希函数建额外哈希表管理所有冲突元素，类似“再哈希法”，通过备用哈希函数分散冲突，是常见策略之一，可以解决。直接覆盖冲突的旧元素，会导致数据丢失，违反哈希表完整性原则，无法解决冲突，所以D.不能解决。故选D。

第10题 以下关于动态规划的说法中，错误的是（   ）。

A. 动态规划方法通常能够列出递推公式。

B. 动态规划方法的时间复杂度通常为状态的个数。

C. 动态规划方法有递推和递归两种实现形式。

D. 对很多问题，递推实现和递归实现动态规划方法的时间复杂度相当。

解析：答案B。动态规划的核心是通过递推公式（状态转移方程）描述子问题与原问题的关系，所以A.正确。动态规划的时间复杂度取决于‌状态数量‌与‌每个状态的计算复杂度‌，通常为O(状态数×单状态计算复杂度)，所以B.错误。‌递归实现‌（自顶向下）：通过记忆化存储避免重复计算，如斐波那契数列的递归解法；‌递推实现‌（自底向上）：通过迭代填充状态表，如数塔问题的递推解法，所以C.正确。两种实现的时间复杂度通常相同，虽然递归会导致指数级别的时间复杂度，因为它会计算许多重复的子问题，但动态规划会存储子问题的结果，来降低复杂度，使其变成多项式级别，但递归可能因函数调用栈产生额外开销，所以D.正确。故选B。

第11题 下面程序的输出为（   ）。

1. #include < iostream>
2. using namespace std;
3. int rec_fib[100];
4. int fib(int n) {
5.     if (n <= 1)
6.         return n;
7.     if (rec_fib[n] == 0)
8.         rec_fib[n] = fib(n - 1) + fib(n - 2);
9.     return rec_fib[n];
10. }
11. int main() {
12.     cout << fib(6) << endl;
13.     return 0;
14. }

A. 8                                       B. 13                                     C. 64                                          D. 结果是随机的

解析：答案A。本题程序实现了一个‌带记忆化（Memoization）的递归斐波那契数列计算‌。斐波那契数列定义‌：fib(0) = 0，fib(1) = 1；fib(n) = fib(n-1) + fib(n-2)（当 n > 1）。

全局数组 rec_fib 用于存储已计算的斐波那契数，避免重复递归调用。若 rec_fib[n] 未被计算过（初始为0），则递归计算并存储结果。计算结果： fib(6)=fib(5)+ fib(4)=5+3=8。

具体递归展开如下：

fib(6) → fib(5) + fib(4) → 5 + 3 = 8

  fib(5) → fib(4) + fib(3) → 3 + 2 = 5 

  fib(4) → fib(3) + fib(2) → 2 + 1 = 3 

    fib(3) → fib(2) + fib(1) → 1 + 1 = 2 

      fib(2) → fib(1) + fib(0) → 1 + 0 = 1 

所以A.正确。故选A。

第 12 题 下面程序的时间复杂度为（   ）。

1. int rec_fib[MAX_N];
2. int fib(int n) {
3.     if (n <= 1)
4.         return n;
5.     if (rec_fib[n] == 0)
6.         rec_fib[n] = fib(n - 1) + fib(n - 2);
7.     return rec_fib[n];
8. }

A. O(2ⁿ)                            B. O(𝜙ⁿ),             C. O(n²)                              D. O(n)

解析：答案D。本题程序使用了‌记忆化递归（Memoization）‌来计算斐波那契数列，rec_fib[n] 数组存储已经计算过的斐波那契数，避免重复计算。

每个 fib(k)（k ∈ [0, n]）‌仅计算一次‌，后续直接查表返回，时间复杂度 ‌O(1)‌。

‌计算 fib(n) 时，会依次计算 fib(n-1), fib(n-2), ..., fib(0)，每个值只计算一次。

总共需要 ‌n 次计算‌（线性增长），因此时间复杂度为 ‌O(n)‌。普通递归的时间复杂度是 ‌O(2ⁿ)‌，因为会重复计算大量子问题。记忆化优化后，递归树退化成‌线性计算链‌，复杂度降为 ‌O(n)‌。普通递归时间复杂度为O(2ⁿ)（或更精确的O(𝜙ⁿ)，𝜙 = (√5 + 1)/2 ≈ 1.618），所以A.、B.错误。无O(n²)这种情况，C.错误。故选‌D‌。

第13题 下面 search 函数的平均时间复杂度为（   ）。

1. int search(int n, int * p, int target) {
2.     int low = 0, high = n;
3.     while (low < high) {
4.         int middle = (low + high) / 2;
5.         if (target == p[middle]) {
6.             return middle;
7.         } else if (target > p[middle]) {
8.             low = middle + 1; }
9.         else {
10.             high = middle;
11.         }
12.     }
13.     return -1;
14. }

A. O(n log(n))                   B. O(n)                             C. O(log(n)                        D. O(1)

解析：答案C。本题的 search 函数明显是‌二分查找（Binary Search）‌算法，其平均时间复杂度为 ‌O(log n)。每次循环将搜索范围缩小一半(middle = (low + high)/2)，通过比较 target 与中间值决定向左或向右继续搜索；若找到目标值则直接返回索引(第5-6行)，否则调整 low 或 high 缩小范围(第7-11行)；每次迭代将数据规模‌n减半，最坏情况下需迭代‌log₂n‌ 次才能确定结果。常见的分治排序算法、快速排序，其时间复杂度O(n log n)，所以A.错误。适用于线性遍历时间复杂度为‌O(log n)，而二分查找无需遍历全部元素，所以B.错误。O(1)仅适用于哈希表等直接访问操作，二分查找需多次比较，做不到O(1)，所以D.错误。故选C。

‌第 14 题 下面程序的时间复杂度为（   ）。

1. int primes[MAXP], num = 0;
2. bool isPrime[MAXN] = {false};
3. void sieve() {
4.     for (int n = 2; n <= MAXN; n++) {
5.         if (!isPrime[n])
6.             primes[num++] = n;
7.         for (int i = 0; i < num && n * primes[i] <= MAXN; i++) {
8.             isPrime[n * primes[i]] = true;
9.             if (n % primes[i] == 0)
10.                 break;
11.         }
12.     }
13. }

A. O(n)                         B. O(n×log n)                      C. O(n×log log n                     D. O(n²)

解析：答案A。本题的程序实现的是‌线性筛法（欧拉筛）‌，用于高效生成素数，其时间复杂度为 ‌O(n)‌（线性复杂度）。外层循环（第 4 行）遍历每个数 n（从 2 到 MAXN）。若 n 未被标记为非素数（!isPrime[n]），则将其加入素数表 primes（第 5-6 行）。内层循环（第 7-11 行）用当前素数 primes[i] 标记合数 n * primes[i]，并在 n 能被 primes[i] 整除时提前终止（第 9-10 行），确保每个合数仅被标记一次。‌每个合数仅被标记一次‌：通过 if (n % primes[i] == 0) break 保证每个合数由其最小素因子标记，避免重复操作。虽然存在嵌套循环，但每个合数的标记操作均摊时间复杂度为 O(1)，总操作次数与 MAXN 成线性关系。‌对比‌埃拉托斯特尼筛法（普通筛）‌：时间复杂度 O(n log log n)，存在重复标记。所以A.正确。故选A。

第15题 下列选项中，哪个不可能是下图的广度优先遍历序列（   ）。

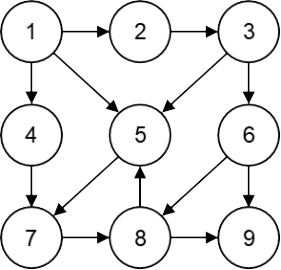
A. 1, 2, 4, 5, 3, 7, 6, 8, 9                                                 B. 1, 2, 5, 4, 3, 7, 8, 6, 9

C. 1, 4, 5, 2, 7, 3, 8, 6, 9                                                 D. 1, 5, 4, 2, 7, 3, 8, 6, 9

解析：答案B。根据广度优先搜索（BFS）的特性，遍历序列应按照层级顺序逐层访问节点，即从起始节点开始，先根节点入列，如有子节点(相邻节点)，则所有子节点(相邻节点)压入队列，依此类推，直到最后一个节点。对A.：先压入①，再压入①的相邻节点②、④、⑤，接着压入②的相邻节点③(⑤已在队列)、④的相邻节点⑦、⑤的相邻节点无(⑦已在队列)，压入③的相邻节点⑥(⑤已在队列)、⑦的相邻节点⑧，最后是⑥的相邻节点⑨。所以广度优先遍历序列1,2,4,5,3,7,6,8,9，所以A.正确。对B.：先压入①，再压入①的相邻节点无②、⑤、④，接着压入②的相邻节点③(⑤已在队列)、⑤的相邻节点⑦、④的相邻节点无(⑦已在队列)，压入③的相邻节点⑥(⑤已在队列)、⑦的相邻节点⑧，最后是⑥的相邻节点⑨。所以广度优先遍历序列1,2,5,4,3,7,6,8,9，不可能出现1, 2, 5, 4, 3, 7, 8, 6, 9，8到达不了6，所以B.错误。对C.：先压入①，再压入①的相邻节点无④、⑤、②，接着压入④的相邻节点⑦、⑤的相邻节点无(⑦已在队列)、②的相邻节点③，压入⑦的相邻节点⑧、③的相邻节点⑥(⑤已在队列)，最后是⑧的相邻节点⑨。所以广度优先遍历序列1,4,5,2,7,3,8,6,9，所以C.正确。对D.：先压入①，再压入①的相邻节点无⑤、④、②，接着压入⑤的相邻节点⑦、④的相邻节点无(⑦已在队列)、②的相邻节点③，压入⑦的相邻节点⑧、③的相邻节点⑥(⑤已在队列)，最后是⑧的相邻节点⑨。所以广度优先遍历序列1,5,4,2,7,3,8,6,9，所以C.正确。故选B。

2 判断题（每题 2 分，共 20 分）

第1题 C++语言中，表达式 9 & 12 的结果类型为 int 、值为 8 。（   ）

解析：答案正确。9 & 12 = 0b00001001 & 0b00001100 = 0b00001000 = 8。故正确。

第2题 C++语言中，指针变量指向的内存地址不一定都能够合法访问。（   ）

‌解析：答案正确。在C++中，指针变量可以指向任意内存地址，但并非所有地址都能被程序合法访问。如：‌未初始化的指针‌：指向随机内存地址，访问可能导致崩溃或数据损坏。‌已释放的内存（野指针）‌：访问delete或free后的内存属于未定义行为。‌空指针（NULL或nullptr）‌：解引用空指针会直接引发段错误。‌越界访问‌：如数组越界或缓冲区溢出，可能破坏其他数据。‌系统保护区域‌：尝试访问操作系统保留地址（如0x00000000）会触发硬件异常。故正确。

第3题 对𝑛个元素的数组进行快速排序，最差情况的时间复杂度为𝑂(𝑛 log 𝑛)。（   ）

解析：答案错误。快速排序的最差时间复杂度为𝑂(𝑛²)，而非𝑂(𝑛 log 𝑛)。故错误。

第4题 一般情况下， long long 类型占用的字节数比 float 类型多。（   ）

‌解析：答案正确‌。在大多数系统中，long long类型占用‌8字节‌，而float类型占用‌4字节。long long类型，固定为8字节（64位），用于存储大范围整数（如−2⁶³ ~ 2⁶³−1）。‌float类型‌

固定为4字节（32位），采用IEEE 754浮点标准存储，范围约为±3.4×10³⁸，但精度有限（约6~7位有效数字）。所以一般情况下long long类型占用的字节数比float类型多。故正确。

第5题 使用math.h或cmath头文件中的函数，表达式pow(10, 3)的结果的值为1000、类型为int。（   ）

解析：答案错误。在C++中，pow(10, 3) 的结果是10的3次幂，即‌1000‌（10³）。

‌pow()函数原型‌：double pow(double base, double exponent);

参数和返回值均为double类型，但整数参数（如10和3）会隐式转换为double计算，所以实际输出通常为1000.0，类型为double。故错误。

第6题 二叉排序树的中序遍历序列一定是有序的。（   ）

解析：答案正确。二叉排序树的定义‌：左子树的所有节点值 ‌小于‌ 当前节点值。右子树的所有节点值 ‌大于‌ 当前节点值。如下图所示。

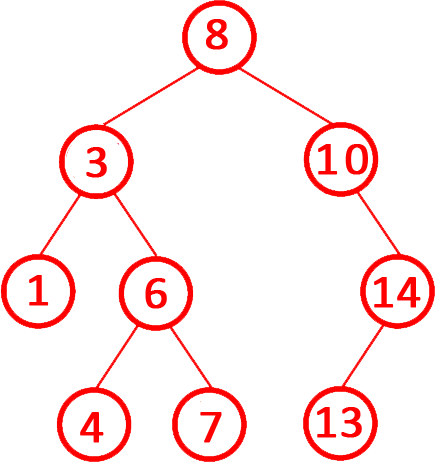
‌中序遍历（左-根-右）的特性‌：先遍历左子树（所有值更小），再访问根节点，最后遍历右子树（所有值更大）。因此，中序遍历结果必然按‌升序排列。故正确。

第7题 无论哈希表采用何种方式解决冲突，只要管理的元素足够多，都无法避免冲突。（   ）

解析：答案正确。哈希函数将较大的输入空间映射到有限的输出空间（哈希表大小），根据鸽巢原理，当元素数量超过哈希表容量时，必然存在多个元素映射到同一位置，即冲突不可避免。即使采用链地址法或开放寻址法等策略，冲突仅被缓解或分散，无法从根本上消除。故正确。

第8题 在C++语言中，类的构造函数和析构函数均可以声明为虚函数。（   ）

解析：答案错误。‌在C++中，构造函数不能是虚函数‌，因为虚函数依赖虚函数表（vtable）实现，而虚函数表在对象构造期间才被初始化。调用构造函数时，对象尚未完全创建，此时无法通过虚函数机制动态绑定。语法上，C++直接禁止构造函数声明为virtual（编译报错）。‌析构函数可以（且有时必须）是虚函数，其作用是当基类指针指向派生类对象时，若基类析构函数非虚，则通过该指针删除对象会导致‌派生类析构未被调用‌，引发资源泄漏。故错误。

第9题 动态规划方法将原问题分解为一个或多个相似的子问题，因此必须使用递归实现。（   ）

解析：答案错误。‌动态规划（Dynamic Programming, DP）的核心思想是通过将原问题分解为‌重叠子问题‌，并存储子问题的解（记忆化）来避免重复计算，从而提高效率。‌关键点‌：子问题必须具有‌重叠性‌和‌最优子结构‌，但实现方式不限定于递归。‌动态规划的两种实现方式‌：‌自顶向下（递归+记忆化）‌：使用递归分解问题，并通过哈希表或数组缓存子问题的解（即“记忆化搜索”）。‌自底向上（迭代）‌：从最小子问题开始，通过迭代逐步构建更大问题的解（通常用数组或表格存储状态）。‌递归并非必需‌。故错误。

第10题 如果将城市视作顶点，公路视作边，将城际公路网络抽象为简单图，可以满足城市间的车道级导航需求。（   ）

解析：答案错误。‌将城市抽象为顶点、公路抽象为边的简单图模型（无向、无权、无自环/重边）无法精确表达车道级导航所需的细节，这是简单图的局限性‌。车道级导航需包含‌车道数量、转向限制、实时交通状态‌等属性，而简单图仅能表示城市间的连通性。‌车道级导航的数据需求‌：高精度导航依赖‌动态权重‌（如实时车速）、‌车道级拓扑‌（如出口车道标识）和‌三维空间关系‌（如高架桥分层），这些无法通过简单图的边和顶点直接建模。故错误。

3 编程题（每题 25 分，共 50 分）

3.1 编程题1

• 试题名称：线图
• 时间限制：1.0 s
• 内存限制：512.0 MB

3.1.1 题目描述

给定由𝑛个结点与𝑚条边构成的简单无向图𝐺，结点依次以1,2,...,𝑛编号。简单无向图意味着 中不包含重边与自环。𝐺的线图𝐿(𝐺)通过以下方式构建：

初始时线图𝐿(𝐺)为空。

对于无向图𝐺中的一条边，在线图𝐺中加入与之对应的一个结点。

对于无向图𝐺中两条不同的边(𝑢₁,𝑣₁),(𝑢₂,𝑣₂)，若存在𝐺中的结点同时连接这两条边（即𝑢₁,𝑣₁之一与𝑢₂,𝑣₂之一相同），则在线图𝐿(𝐺)中加入一条无向边，连接(𝑢₁,𝑣₁),(𝑢₂,𝑣₂)在线图中对应的结点。

请你求出线图𝐿(𝐺)中所包含的无向边的数量。

3.1.2 输入格式

第一行，两个正整数𝑛,𝑚，分别表示无向图𝐺中的结点数与边数。

接下来𝑚行，每行两个正整数𝑢ᵢ,𝑣ᵢ，表示𝐺中连接𝑢ᵢ,𝑣ᵢ的一条无向边。

3.1.3 输出格式

输出共一行，一个整数，表示线图𝐿(𝐺)中所包含的无向边的数量。

3.1.4 样例

3.1.4.1 输入样例1

1. 5 4
2. 1 2
3. 2 3
4. 3 1
5. 4 5

3.1.4.2 输出样例1

1. 3

3.1.4.3 输入样例2

1. 5 10
2. 1 2
3. 1 3
4. 1 4
5. 1 5
6. 2 3
7. 2 4
8. 2 5
9. 3 4
10. 3 5
11. 4 5

3.1.4.4 输出样例2

1. 30

3.1.4.5 样例解释

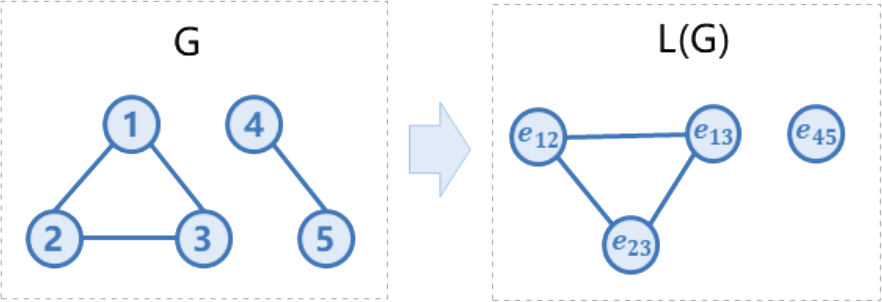
3.1.5 数据范围

对于60%的测试点，保证1≤𝑛≤500，1≤𝑚≤500。 对于所有测试点，保证1≤𝑛≤10⁵，1≤𝑚≤10⁵。

3.1.6 编写程序思路

分析：设计思路与原理：‌线图定义：线图L(G) 的顶点对应原图G 的边。若原图G 中两条边共享一个公共顶点，则在线图L(G) 中对应的顶点之间连一条边。线图的边数等于原图中所有共享公共顶点的边对数。对于原图的每个顶点u，其邻接边的数量为edge(u)，贡献的边对数为​。构建邻接表，记录每个顶点的邻接边。遍历每个顶点，计算其邻接边的组合数并累加。‌时间复杂度‌：邻接表构建：O(m)，组合数计算：O(n)，总复杂度：O(n+m)。因为n≤10⁵，m≤10⁵，总复杂度在10⁵数量级，不会超时。完整参考程序代码如下：

#include <iostream>
using namespace std;const int MaxN = 1e5+10; //顶点编号n≤10⁵
int n, m, edge[MaxN];    //顶点编号1~n，初始为0int main() {cin >> n >> m;for (int i = 1; i <= m; ++i) { //输入m条边uᵢ,vᵢint u, v;cin >> u >> v;edge[u]++;  //顶点计数edge[v]++;  //顶点计数}long long edge_count = 0;  //防止大数溢出for (int u = 1; u <= n; ++u)edge_count += 1ll * edge[u] * (edge[u] - 1) / 2; //组合运算cout << edge_count << endl;return 0;
}

3.2 编程题2

• 试题名称：调味平衡
• 时间限制：1.0 s
• 内存限制：512.0 MB

3.2.1 题目描述

小A准备了𝑛种食材用来制作料理，这些食材依次以1,2,...,𝑛编号，第i种食材的酸度为aᵢ，甜度为bᵢ。对于每种食材，小A可以选择将其放入料理，或者不放入料理。料理的酸度𝐴为放入食材的酸度之和，甜度𝐵为放入食材的甜度之和。如果料理的酸度与甜度相等，那么料理的调味是平衡的。 过于清淡的料理并不好吃，因此小A想在满足料理调味平衡的前提下，合理选择食材，最大化料理的酸度与甜度之和。你能帮他求出在调味平衡的前提下，料理酸度与甜度之和的最大值吗？

3.2.2 输入格式

第一行，一个正整数𝑛，表示食材种类数量。

接下来𝑛行，每行两个正整数aᵢ, bᵢ，表示食材的酸度与甜度。

3.2.3 输出格式

输出共一行，一个整数，表示在调味平衡的前提下，料理酸度与甜度之和的最大值。

3.2.4 样例

3.2.4.1 输入样例1

1. 3
2. 1 2
3. 2 4
4. 3 2

3.2.4.2 输出样例1

1. 8

3.2.4.3 输入样例2

1. 5
2. 1 1
3. 2 3
4. 6 1
5. 8 2
6. 5 7

3.2.4.4 输出样例2

1. 2

3.2.5 数据范围

对于40%的测试点，保证1≤𝑛≤10，1≤aᵢ, bᵢ≤10。

对于另外20%的测试点，保证1≤𝑛≤50，1≤aᵢ, bᵢ≤10。

对于所有测试点，保证1≤𝑛≤100，1≤aᵢ, bᵢ≤500。

3.2.6 编写程序思路

方法一：用vector(可变数组存放料理酸度与甜度， 不会vector也可用结构体struct)。需要选择若干食材，使得它们的总酸度等于总甜度（A = B），同时最大化A + B（即2A或2B）。

这是一个典型的‌动态规划‌问题，可以转化为‌背包问题‌的变种：我们需要跟踪酸度和甜度的差值（A - B），并记录对应的最大总和（A + B）。用‌动态规划设计，‌状态定义‌：dp[d] 表示酸度与甜度之差为 d 时的最大总和（A + B）。‌初始化‌：dp[0] = 0（差值为0时总和为0），其他状态初始化为负无穷（表示不可达）。‌状态转移‌：对于每个食材，更新所有可能的差值 d：

如果选择该食材，新的差值为 d + (aᵢ - bᵢ)，新的总和为 dp[d] + aᵢ + bᵢ。不选择则保持原状态。偏移量处理‌：由于差值可能为负，使用偏移量将差值映射到非负范围。‌复杂度优化‌，使用滚动数组或一维数组优化空间复杂度。差值范围限制在 [-sum(aᵢ + bᵢ), sum(aᵢ + bᵢ)] 内，避免无效计算。时间复杂度O(n*MAX_DIFF)=100*105*505*2≈10⁷，不会超时。完整参考程序代码如下：

#include <iostream>
#include <vector>
using namespace std;const int MAX_DIFF = 105 * 505 * 2; //n*a*2，最大可能差值范围
const int OFFSET = MAX_DIFF / 2;    //偏移量处理负值(中心点)int main() {ios::sync_with_stdio(false); //即取消缓冲区同步，cin、cout效率接近scanf、printfcin.tie(nullptr);            //解除cin和cout之间的绑定，进一步加快执行效率int n;cin >> n;vector<pair<int, int >> items(n); //pair成对数据.first存酸度a、.second存甜度bfor (int i = 0; i < n; ++i) {cin >> items[i].first >> items[i].second; //输入n个酸度、甜度对}vector<int> dp(MAX_DIFF + 1, -1000); //1≤aᵢ,bᵢ≤500。aᵢ-bᵢ≥-499dp[OFFSET] = 0; // 初始状态：差值为0时和为0for (const auto& item : items) {int a = item.first, b = item.second;int diff = a - b;vector<int> new_dp = dp; //拷贝创建new_dp，dp的所有元素复制到new_dpfor (int j = 0; j <= MAX_DIFF; ++j) {if (dp[j] != -1000) {int new_j = j + diff;if (new_j >= 0 && new_j <= MAX_DIFF) {if (new_dp[new_j] < dp[j] + a + b) {new_dp[new_j] = dp[j] + a + b;}}}}dp = move(new_dp); //资源所有权的转移给dp，new_dp.size()=0}cout << max(0, dp[OFFSET]) << endl;return 0;
}

方法二：用一个动态规划算法，主要功能是处理输入数据并计算特定条件下的最大值。数组dp[MAX_DIFF+1]初始化为极小值(-16843010<-499)，仅dp[OFFSET]初始化为0，作为动态规划的起点。核心算法：先读取n对整数(a,b)，计算addt=a+b和subt=a-b‌，根据subt值的正负采用不同的遍历方向：subt≤0时正向遍历更新dp数组，subt>0时逆向遍历更新dp数组，通过max(dp[j+subt], dp[j]+addt)实现状态转移，记录最大值，‌输出结果为最终输出dp[OFFSET]的值，即中心位置的计算结果‌。使用动态规划思想，通过状态转移方程更新数组值‌；采用双指针技巧处理不同方向的遍历需求。时间复杂度O(n*n*a*2)=100*105*505*2‌≈10⁷，不会超时。完整参考程序代码如下：

‌#include <iostream>
#include <cstring> //含memset()函数
using namespace std;const int MAX_DIFF = 105 * 505 * 2; //n*a*2，最大可能差值范围
const int OFFSET = MAX_DIFF / 2;    //偏移量处理负值(中心点)int main() {ios::sync_with_stdio(false); //即取消缓冲区同步，cin、cout效率接近scanf、printfcin.tie(nullptr);            //解除cin和cout之间的绑定，进一步加快执行效率int n;cin >> n;int dp[MAX_DIFF + 1]; //1≤aᵢ,bᵢ≤500。aᵢ-bᵢ≥-499memset(dp, -2, sizeof(dp)); //初始化为-16843010。0b11111110111111101111111011111110dp[OFFSET] = 0; // 初始状态：差值为0时和为0for (int i = 0; i < n; ++i) {int a, b;cin >> a >> b;                  //输入n个数据对int addt = a + b, sunt = a - b; //求和及差if (sunt <= 0)   //小于等于0，正向遍历for (int j = -sunt; j <= MAX_DIFF; ++j)dp[j + sunt] = max(dp[j + sunt], dp[j] + addt);else             //否则大于0，逆向遍历for (int j = MAX_DIFF - sunt - 1; j; j--)dp[j + sunt] = max(dp[j + sunt], dp[j] + addt);}cout << max(0, dp[OFFSET]) << endl;return 0;
}