Python 线性回归详解:从原理到实战
线性回归(Linear Regression)是机器学习中最基础也是最重要的算法之一,广泛应用于预测分析领域,例如房价预测、销售额预测等。本文将带你从理论出发,用 Python 手把手实现线性回归,助你迈出机器学习实战第一步。
一、线性回归是什么?
线性回归是一种用于预测目标变量(因变量)与一个或多个特征变量(自变量)之间关系的模型,其核心思想是拟合一条“最佳直线”:
y=w1x1+w2x2+⋯+wnxn+b
其中:
y:预测值
x1,x2,…,xn:特征
w1,w2,…,wn:系数(权重)
b:截距项
二、使用 sklearn 实现一元线性回归
我们从简单的一元线性回归入手,使用 scikit-learn 库实现。
先创建一个csv数据:
import csv# 数据
data = [["广告投入", "销售额"],[29, 77],[28, 62],[34, 93],[31, 84],[25, 59],[29, 64],[32, 80],[31, 75],[24, 58],[33, 91],[25, 51],[31, 73],[26, 65],[30, 84]
]# 创建 CSV 文件并写入数据
with open('test1.csv', 'w', newline='', encoding='utf-8') as csvfile:writer = csv.writer(csvfile)writer.writerows(data)
实现一元线性回归:
此代码看似长,其实是因为打印了很多数据和注释,为了让初学者加深了解。
实际作用代码就几行
import pandas as pd
from sklearn.linear_model import LinearRegression
import numpy as npdata = pd.read_csv("data.csv")
# 准备训练数据:X为特征矩阵(所有列除了"销售额"),y为目标变量("销售额")
X = data.drop("销售额",axis=1) # 特征矩阵
y = data[["销售额"]] # 目标变量# 创建线性回归模型实例
# 使用特征矩阵X和目标变量y训练线性回归模型
lr_model = LinearRegression()
lr_model.fit(X,y)# 计算"广告投入"和"销售额"两列之间的相关系数矩阵
corr = data[["广告投入","销售额"]].corr() # 关系系数矩阵
print(corr)
print("-----")# 计算模型在训练数据上的拟合优度(R²值),评估模型性能
score = lr_model.score(X,y)
print(f"模型拟合优度(R²): {score}")# 获取模型参数:a为自变量系数(斜率),b为截距(偏置)
a = lr_model.coef_
b = lr_model.intercept_
print(f"自变量系数: {a}")
print(f"截距: {b}")# 打印线性回归方程
print(f"线性回归模型为: y = {a[0][0]:.2f}x1 + {b[0]:.2f}")# 预测广告投入为28时的销售额
print(f"当广告投入为28时,预测销售额为: {lr_model.predict([[28]])}")import matplotlib.pyplot as plt
# 生成用于绘制回归线的新数据点(广告投入范围从24到39)
# 使用模型预测新数据点对应的销售额
x_new = np.arange(20, 40).reshape(-1, 1)
y_new = lr_model.predict(x_new)
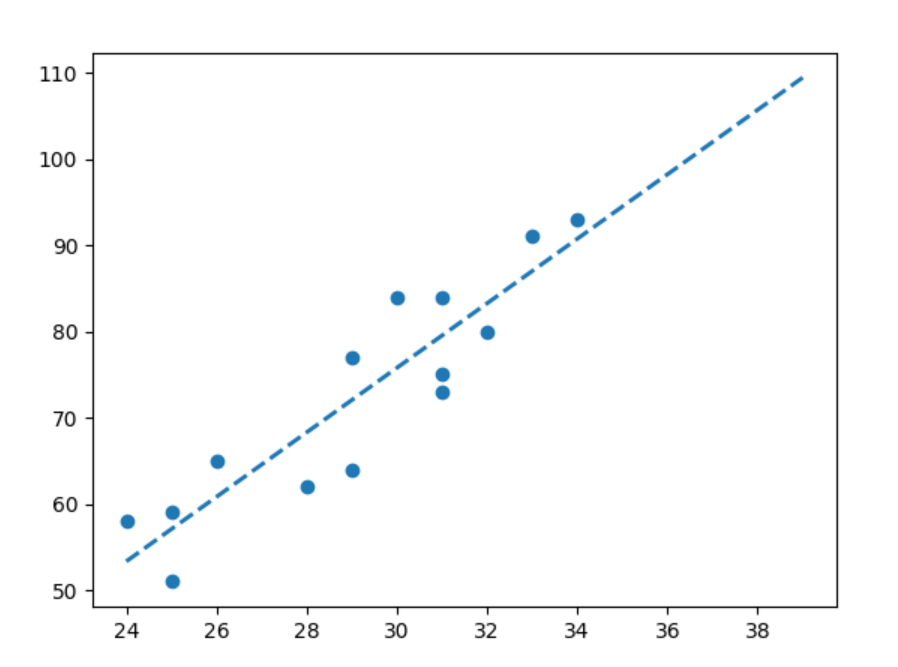
# 绘制回归线
plt.plot(x_new, y_new, '--', color='#1F77B4', linewidth=2)
# 绘制散点图
plt.scatter(X,y)
plt.show()三、多元线性回归示例
如果有多个特征变量:
创建数据:
import csvdata = [["体重", "年龄", "血压收缩"],[76.0, 50, 120],[91.5, 20, 141],[85.5, 20, 124],[82.5, 30, 126],[79.0, 30, 117],[80.5, 50, 125],[74.5, 60, 123],[79.0, 50, 125],[85.0, 40, 132],[76.5, 55, 123],[82.0, 40, 132],[95.0, 40, 155],[92.5, 20, 147]
]with open('test2.csv', 'w', newline='') as csvfile:writer = csv.writer(csvfile)writer.writerows(data)多元线性回归示例:
import pandas as pd
from sklearn.linear_model import LinearRegression# 导入数据
data = pd.read_csv("test2.csv", encoding='gbk', engine='python')# 打印相关系数矩阵
corr = data[["体重", "年龄", "血压收缩"]].corr()
print("相关系数矩阵:")
print(corr)# 第二步,估计模型参数,建立回归模型
lr_model = LinearRegression()
x = data[['体重', '年龄']]
y = data['血压收缩']# 训练模型
lr_model.fit(x, y)# 第四步,对回归模型进行检验
score = lr_model.score(x, y) # 利用 score 方法获取模型拟合优度(R²)
print("模型拟合优度(R²):", score)# 第五步,利用回归模型进行预测
print("预测结果 1:", lr_model.predict([[80, 60]]))
print("预测结果 2:", lr_model.predict([[70, 30], [70, 20]]))# 获取自变量系数和截距
a = lr_model.coef_
b = lr_model.intercept_
print("线性回归模型为: y = {:.2f}x1 + {:.2f}x2 + {:.2f}".format(a[0], a[1], b))
四、模型评估:R² 分数
线性回归模型的评估通常使用决定系数 R2:
r2 = model.score(X, y)
print(f"模型 R² 分数: {r2:.2f}")
R2=1:完美预测
R2=0:模型没有预测能力
R2<0:预测还不如使用平均值
五、相关系数矩阵
相关系数矩阵(Correlation Matrix)是描述多个变量之间两两线性相关程度的矩阵,通常使用皮尔逊相关系数(Pearson Correlation Coefficient)来衡量。
一、皮尔逊相关系数公式
皮尔逊相关系数 rrr 公式如下:
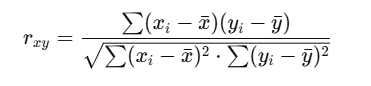
其取值范围为:
r=1:完全正相关
r=−1:完全负相关
r=0:无线性关系
二、相关系数的解释
| 相关系数范围 | 线性相关强度 | 解释 |
|---|---|---|
| 0.9 ~ 1.0 | 极强正相关 | 几乎严格线性关系 |
| 0.7 ~ 0.9 | 强正相关 | 明显线性趋势 |
| 0.5 ~ 0.7 | 中等正相关 | 有一定线性趋势 |
| 0.3 ~ 0.5 | 弱正相关 | 稍有线性趋势 |
| 0.0 ~ 0.3 | 极弱或无相关 | 几乎无线性关系 |
| < 0 | 负相关 | 越小,反向关系越强 |
六、几点注意事项
特征缩放:当特征尺度差异较大时,应使用
StandardScaler进行归一化或标准化。共线性问题:特征之间高度相关可能导致模型不稳定。
异常值:极端值会显著影响回归线。
残差分析:拟合后应分析残差是否符合正态分布。
七、总结
线性回归是回归分析的入门基础;
使用
sklearn.linear_model.LinearRegression可以快速构建模型;可以可视化预测结果和分析模型性能;
推荐在实际应用中注重数据预处理、特征选择与残差分析。
)




)




)








