还记得你第一次做出Meta分析时的成就感吗？那种从海量文献中抽丝剥茧，最终得出可靠结论的感觉，简直不要太爽！
但是，时代在进步，科研在卷动，Meta分析也有它的"升级版"——伞状Meta分析！
在医学研究领域，每天都有海量新证据涌现。如何快速判断某个结论是否可靠？当面对同一问题的数十篇Meta分析时，临床医生该信哪一篇？
答案或许藏在“伞状Meta分析”中——它被誉为“证据金字塔尖的整合者”，能一键穿透争议迷雾，告诉你真正的高质量结论。
什么是伞状Meta分析？
伞状meta分析（Umbrella Review）是一种系统性评估方法，用于综合评价某一领域内多个meta分析的结果。它通过整合多个相关meta分析的证据，提供更全面的结论，适用于复杂或存在争议的研究领域。
为什么现在必须学伞状Meta？
近年来，随着学术研究的不断深入和扩展，使用“umbrella review”、“systematic reviews of systematic reviews”、“umbrella systematic review”等关键词在Web of Science数据库中的检索结果显示，伞形综述（umbrella reviews）相关文献的发表数量呈现出显著的逐年增长趋势（如图所示）。这一趋势充分反映了该领域研究的蓬勃发展，并表明伞形综述正日益受到学术界的广泛关注和重视。
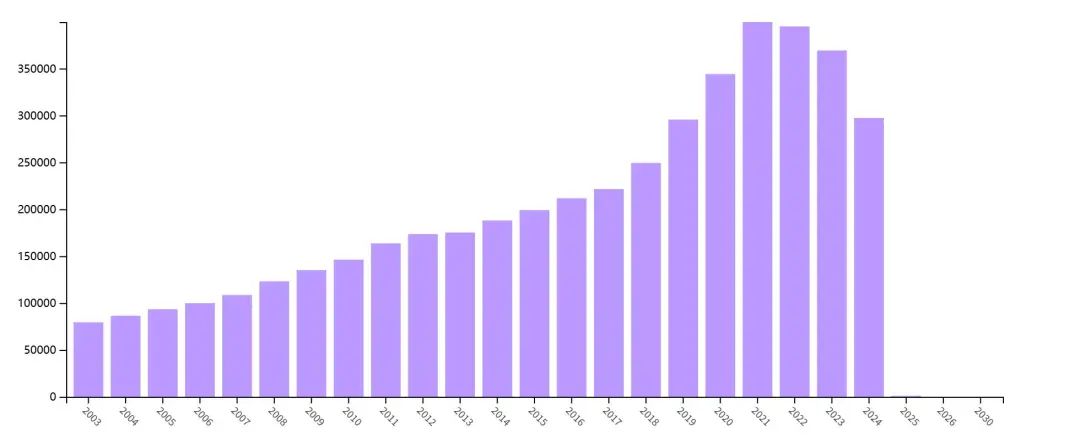为什么现在必须学伞状Meta？
🔥 证据更强：相比传统Meta分析，结论更可靠
🔥 省时省力：1篇伞状Meta ≈ 多篇传统Meta
🔥 创新性强：国际顶刊趋势，发文潜力巨大
🔥 工具成熟：首套完整方法论+实操工具包
今天，小优以下面这篇文献跟大家分享一下此类课题的技术路线。
题目：癌症患者疼痛、抑郁及焦虑的全球患病率与决定因素：系统评价和Meta分析的伞状综述
杂志：BMC Psychiatry
影响因子：IF=3.4
中科院分区：医学二区
发表时间：2025年2月
Part 1：研究背景
抑郁、焦虑和痛苦是相互关联的心理和身体状况，它们共同影响个人的整体健康状况。这些疾病会形成一个恶性循环，其中每个疾病都会放大另一个，导致生活质量的严重下降。对于癌症幸存者来说，他们诊断和治疗的情绪环与持续的心理压力相联系，会加剧身体痛苦，使人难以管理精神和身体症状。基于此，本研究通过伞状综述方法，系统评估全球范围内癌症患者疼痛、抑郁及焦虑症状的流行病学特征，并整合其关键生物-心理-社会决定因素。
Part 2：方法学
文献检索
本研究检索于2024年7月1日至15日进行，涵盖以下数据库：MEDLINE、EMBASE、CINAHL、PubMed、ScienceDirect、Web of Science、Cochrane系统评价数据库及PROSPERO（国际前瞻性系统评价注册库）。
结局变量的测量
本伞状综述聚焦三大核心结局指标：疼痛、抑郁与焦虑。疼痛评估采用多维测量工具组合策略，包括：
视觉模拟评分法（VAS）
数字评分法（NRS）
语言评分法（VRS）
二分类疼痛判定法（是/否）
针对采用VAS/NRS报告的疼痛程度数据，本研究引入Serlin分级标准进行疼痛强度分层（如：轻度≤3分，中度4-6分，重度≥7分）。在心理症状评估方面，采用医院焦虑抑郁量表（HADS）与患者健康问卷（PHQ）双量表验证模式，确保癌症患者焦虑抑郁状态的精准识别。此外，本综述通过跨文化视角系统解析全球范围内癌症患者焦虑与抑郁的生物-社会-临床决定因素谱系。
偏倚风险评估
本研究采用系统评价方法学质量评估工具（AMSTAR）对纳入的每项系统评价与Meta分析（SRMA）进行双重质量核查，确保其方法学严谨性与证据可靠性。
Part 3：分析结果
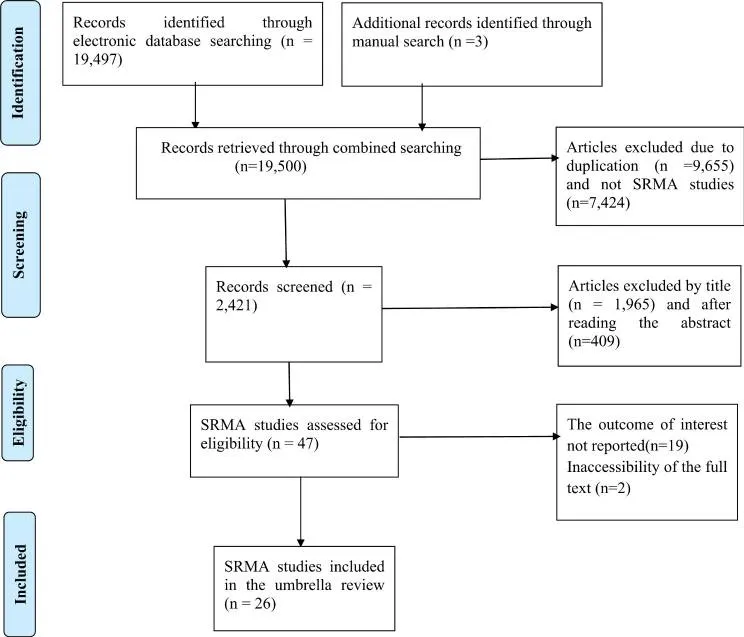
文献检索结果
最终，本伞状综述纳入26项系统评价与Meta分析（SRMA）研究。
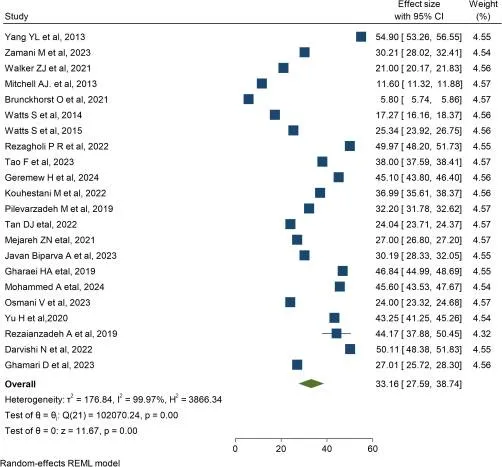
抑郁症的患病率
全球癌症幸存者抑郁症状汇总患病率为33.16%（95% CI 27.59–38.74）。异质性分析显示I²指数达99.7%（p<0.001），提示极高异质性。漏斗图不对称分布提示潜在发表偏倚，Egger检验（p=0.001）证实此偏倚，表明阴性/中性结果的小型研究可能未被充分发表。通过Trim and Fill分析填补12项潜在缺失研究后，校正后抑郁患病率降至12.03%（95% CI 6.41–17.65），较原始值下降63.7%，提示未发表研究可能显著影响原始结果的高估。
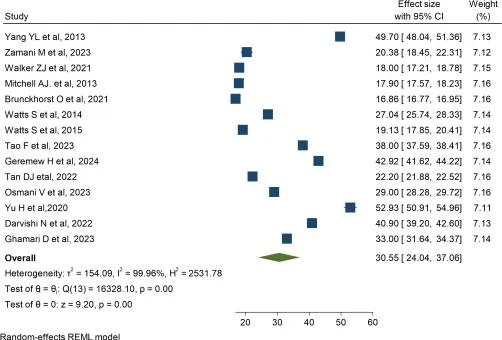
焦虑症的患病率
全球癌症幸存者焦虑症状汇总患病率为30.55%（95% CI 24.04–37.06）。异质性分析显示I²指数高达99.96%（p<0.001），提示研究间存在极端异质性。Egger检验（p<0.001）与漏斗图不对称性证实存在显著发表偏倚，暗示小样本或阴性结果研究可能未被充分发表。通过Trim and Fill分析填补8项潜在缺失研究后，焦虑患病率修正为17.80%（95% CI 13.18–22.41），较原始值下降41.7%，表明未发表研究导致原始结果系统性高估。
疼痛的发生率
本伞状综述系统解析了全球癌症幸存者的疼痛患病率，涵盖治疗前、治疗期间及治疗后的疼痛动态演变。数据显示：
治疗前：近2/3患者（65.22%，95% CI 62.86–67.57）存在疼痛症状。
治疗期间：51.34%（95% CI 40.01–62.67）患者仍受疼痛困扰。
治疗后：39.77%（95% CI 31.84–47.70）幸存者存在持续性疼痛。
整体趋势表明，癌症治疗可降低疼痛发生率，但近四成幸存者在治疗结束后仍受疼痛影响，提示现行疼痛管理策略存在"疗效衰减窗口"。
Part 4：讨论
本伞状综述揭示癌症幸存者心理健康与疼痛负担严峻：抑郁、焦虑及治疗后疼痛的全球患病率分别为33.16%、30.55%和39.77%，其中治疗前疼痛率高达65.22%。核心风险因素包括疾病复发恐惧、治疗副作用及社会支持缺失，同时存在显著地域与人群差异（如亚洲患者心理症状报告率低于欧美）。研究强调需构建整合心理干预-疼痛管理-长期监测的跨学科照护体系，并为优化临床指南（如制定分阶段疼痛控制路径）及公共卫生政策（如增加心理健康服务资源配置）提供循证依据。
Part 5：小优结语
伞状Meta分析揭示癌症幸存者真实负担：比如校正偏倚后抑郁率骤降（33%→12%），凸显其整合证据、识别偏倚的核心价值。它不仅是数据校正器，更是临床决策的指南针——指导精准干预，重塑从“生存”到“生活”的癌症康复体系。
为什么伞状meta被称为“证据天花板”？
✅ 广度MAX：横跨所有相关Meta分析，避免“只见树木不见森林”
✅ 权威性MAX：仅纳入高质量研究，用AMSTAR等工具严筛证据
✅ 结论可视化：通过分级系统（如GRADE）标记证据等级，红黄绿灯一目了然
（举个栗子🌰）
某疾病有20篇Meta分析探讨维生素D的疗效，结论却互相矛盾。伞状分析可统一评估：
哪些剂量真正有效？（如2000IU/天改善骨密度：证据A级）
哪些声称的“副作用”其实证据薄弱？（如“导致肾损伤”：证据D级）
哪些场景必须用它？
🔍 临床决策纠结时：当指南推荐存在冲突
🔍 科研选题迷茫时：快速定位领域内最强证据缺口
🔍 政策制定争议时：用全景证据支持资源分配
经典案例：
《英国医学杂志》（BMJ）曾用伞状分析揭秘“营养神药”真相——综合530篇Meta分析后发现，80%的膳食补充剂对健康人无益， Omega-3、维生素D等仅对特定人群有效。
未来已来，你准备好“撑伞”了吗？
在循证医学的暴雨中，伞状Meta分析正成为临床、科研、政策领域的**“决策导航仪”。
)
