题目描述

给定一个 N 叉树，返回其节点值的层序遍历。（即从左到右，逐层遍历）。

树的序列化输入是用层序遍历，每组子节点都由 null 值分隔（参见示例）。

示例 1：

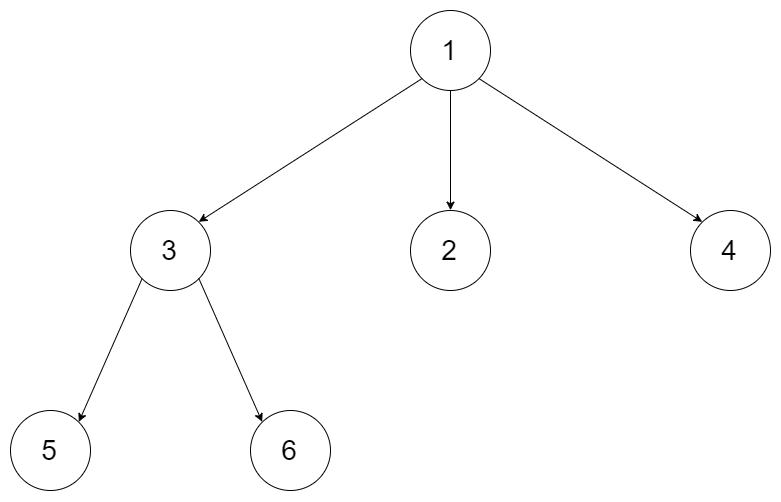
输入：root = [1,null,3,2,4,null,5,6]
输出：[[1],[3,2,4],[5,6]]

示例 2：

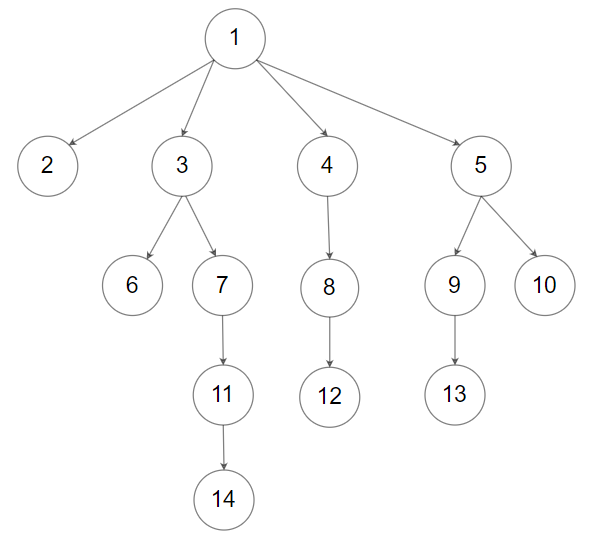
输入：root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
输出：[[1],[2,3,4,5],[6,7,8,9,10],[11,12,13],[14]]

提示：

• 树的高度不会超过 1000

• 树的节点总数在 [0, 10^4] 之间

---

问题分析

这是一道典型的树的层序遍历问题。与二叉树的层序遍历相比，N叉树的特点是每个节点可以有任意数量的子节点。

要求：

1. 按照层级顺序遍历树（从上到下，从左到右）

2. 每一层的节点值要分组返回

3. 需要区分不同的层级

思路：

• 使用广度优先搜索（BFS）是最直观的解法

• 也可以使用深度优先搜索（DFS），配合层级信息

• 需要记录每个节点所在的层级

---

解题思路

方法一：广度优先搜索（BFS）

BFS是解决层序遍历问题的经典方法，因为BFS天然按照层级顺序访问节点。

算法步骤：

1. 使用队列存储节点，队列的特性保证了先进先出的层序访问

2. 每次处理队列中的所有节点（即当前层的所有节点）

3. 在处理当前层节点时，将它们的子节点加入队列（为下一层做准备）

4. 记录每一层的节点值

优势：

• 逻辑直观，容易理解

• 代码结构清晰

• 时间复杂度优秀

方法二：深度优先搜索（DFS）

DFS通过递归的方式遍历树，同时记录当前节点的层级信息。

算法步骤：

1. 递归遍历每个节点

2. 传递层级参数，记录当前节点所在的层

3. 根据层级将节点值放入对应的结果列表中

4. 递归处理所有子节点

优势：

• 代码简洁

• 不需要额外的队列数据结构

• 递归思维自然

---

算法图解

以示例1为例：root = [1,null,3,2,4,null,5,6]

树结构：1/  |  \3   2   4/ \5   6

BFS执行过程：

1. 初始状态：队列 = [1]，结果 = []

2. 第1层：

   • 处理节点1，当前层 = [1]

   • 将节点1的子节点加入队列：队列 = [3,2,4]

   • 结果 = [[1]]

3. 第2层：

   • 处理节点3,2,4，当前层 = [3,2,4]

   • 将节点3的子节点加入队列：队列 = [5,6]

   • 结果 = [[1],[3,2,4]]

4. 第3层：

   • 处理节点5,6，当前层 = [5,6]

   • 没有子节点，队列为空

   • 结果 = [[1],[3,2,4],[5,6]]

DFS执行过程：

1. 访问节点1（level=0）：result[0] = [1]

2. 访问节点3（level=1）：result[1] = [3]

3. 访问节点5（level=2）：result[2] = [5]

4. 访问节点6（level=2）：result[2] = [5,6]

5. 访问节点2（level=1）：result[1] = [3,2]

6. 访问节点4（level=1）：result[1] = [3,2,4]

---

详细代码实现

Java 实现

Java N叉树节点定义

// Java N叉树节点定义
class Node {public int val;public List<Node> children;public Node() {}public Node(int _val) {val = _val;}public Node(int _val, List<Node> _children) {val = _val;children = _children;}
}

BFS 方法

import java.util.*;class Solution {public List<List<Integer>> levelOrder(Node root) {List<List<Integer>> result = new ArrayList<>();// 边界条件检查if (root == null) {return result;}// 使用队列进行广度优先搜索Queue<Node> queue = new LinkedList<>();queue.offer(root);while (!queue.isEmpty()) {// 当前层的节点数量int levelSize = queue.size();// 当前层的节点值列表List<Integer> currentLevel = new ArrayList<>();// 处理当前层的所有节点for (int i = 0; i < levelSize; i++) {Node currentNode = queue.poll();currentLevel.add(currentNode.val);// 将当前节点的所有子节点加入队列if (currentNode.children != null) {for (Node child : currentNode.children) {queue.offer(child);}}}// 将当前层的结果加入最终结果result.add(currentLevel);}return result;}
}

DFS 方法

import java.util.*;class Solution {public List<List<Integer>> levelOrder(Node root) {List<List<Integer>> result = new ArrayList<>();// 边界条件检查if (root == null) {return result;}// 从根节点开始DFS，初始层级为0dfs(root, 0, result);return result;}private void dfs(Node node, int level, List<List<Integer>> result) {// 如果是新的层级，需要创建新的列表if (level >= result.size()) {result.add(new ArrayList<>());}// 将当前节点的值加入对应层级的列表result.get(level).add(node.val);// 递归处理所有子节点，层级加1if (node.children != null) {for (Node child : node.children) {dfs(child, level + 1, result);}}}
}

C# 实现

C# N叉树节点定义

// C# N叉树节点定义
public class Node {public int val;public IList<Node> children;public Node() {}public Node(int _val) {val = _val;}public Node(int _val, IList<Node> _children) {val = _val;children = _children;}
}

BFS 方法

using System.Collections.Generic;public class Solution {public IList<IList<int>> LevelOrder(Node root) {IList<IList<int>> result = new List<IList<int>>();// 边界条件检查if (root == null) {return result;}// 使用队列进行广度优先搜索Queue<Node> queue = new Queue<Node>();queue.Enqueue(root);while (queue.Count > 0) {// 当前层的节点数量int levelSize = queue.Count;// 当前层的节点值列表IList<int> currentLevel = new List<int>();// 处理当前层的所有节点for (int i = 0; i < levelSize; i++) {Node currentNode = queue.Dequeue();currentLevel.Add(currentNode.val);// 将当前节点的所有子节点加入队列if (currentNode.children != null) {foreach (Node child in currentNode.children) {queue.Enqueue(child);}}}// 将当前层的结果加入最终结果result.Add(currentLevel);}return result;}
}

DFS 方法

using System.Collections.Generic;public class Solution {public IList<IList<int>> LevelOrder(Node root) {IList<IList<int>> result = new List<IList<int>>();// 边界条件检查if (root == null) {return result;}// 从根节点开始DFS，初始层级为0Dfs(root, 0, result);return result;}private void Dfs(Node node, int level, IList<IList<int>> result) {// 如果是新的层级，需要创建新的列表if (level >= result.Count) {result.Add(new List<int>());}// 将当前节点的值加入对应层级的列表result[level].Add(node.val);// 递归处理所有子节点，层级加1if (node.children != null) {foreach (Node child in node.children) {Dfs(child, level + 1, result);}}}
}

---

复杂度分析

BFS方法

• 时间复杂度：O(n)，其中n是树中节点的总数。每个节点恰好被访问一次。

• 空间复杂度：O(n)，主要是队列和结果数组的空间开销。最坏情况下，队列中可能存储接近n/2个节点（最底层）。

DFS方法

• 时间复杂度：O(n)，每个节点恰好被访问一次。

• 空间复杂度：O(h)，其中h是树的高度。主要是递归调用栈的深度，最坏情况下为O(n)（退化为链状树）。