一、搜索

1. 什么是搜索？

搜索，是一种枚举，通过穷举所有的情况来找到最优解，或者统计合法解的个数。因此，搜索有时候也叫作暴搜。 搜索一般分为深度优先搜索 (DFS) 与宽度优先搜索 (BFS) 。

2. 遍历 vs 搜索

深度优先遍历 vs 深度优先搜索，宽度优先遍历 vs 宽度优先搜索？遍历是形式，搜索是目的。 不过，在一般情况下，我们不会去纠结概念的差异，两者可以等同。

3. 回溯与剪枝

回溯：当在搜索的过程中，遇到走不通或者走到底的情况时，就回头。

剪枝：剪掉在搜索过程中，重复出现或者不是最优解的分支。

---

二、OJ 练习

1. 枚举子集 ⭐

【题目链接】

B3622 枚举子集（递归实现指数型枚举） - 洛谷

【题目描述】

今有 $n$ 位同学，可以从中选出任意名同学参加合唱。

请输出所有可能的选择方案。

【输入格式】

仅一行，一个正整数 $n$。

【输出格式】

若干行，每行表示一个选择方案。

每一种选择方案用一个字符串表示，其中第 $i$ 位为 Y 则表示第 $i$ 名同学参加合唱；为 N 则表示不参加。

需要以字典序输出答案。

【示例一】

输入

3

输出

NNN
NNY
NYN
NYY
YNN
YNY
YYN
YYY

【说明/提示】

对于 $100\%$ 的数据，保证 $1\le n\le 10$。

---

(1) 解题思路

对于题目中给的示例来说，我们一共有 3 个人，也就是说我们有三个字母需要填，那么对于每一个字母都有两种情况，我们不妨画出一个树状图来展示枚举的过程。

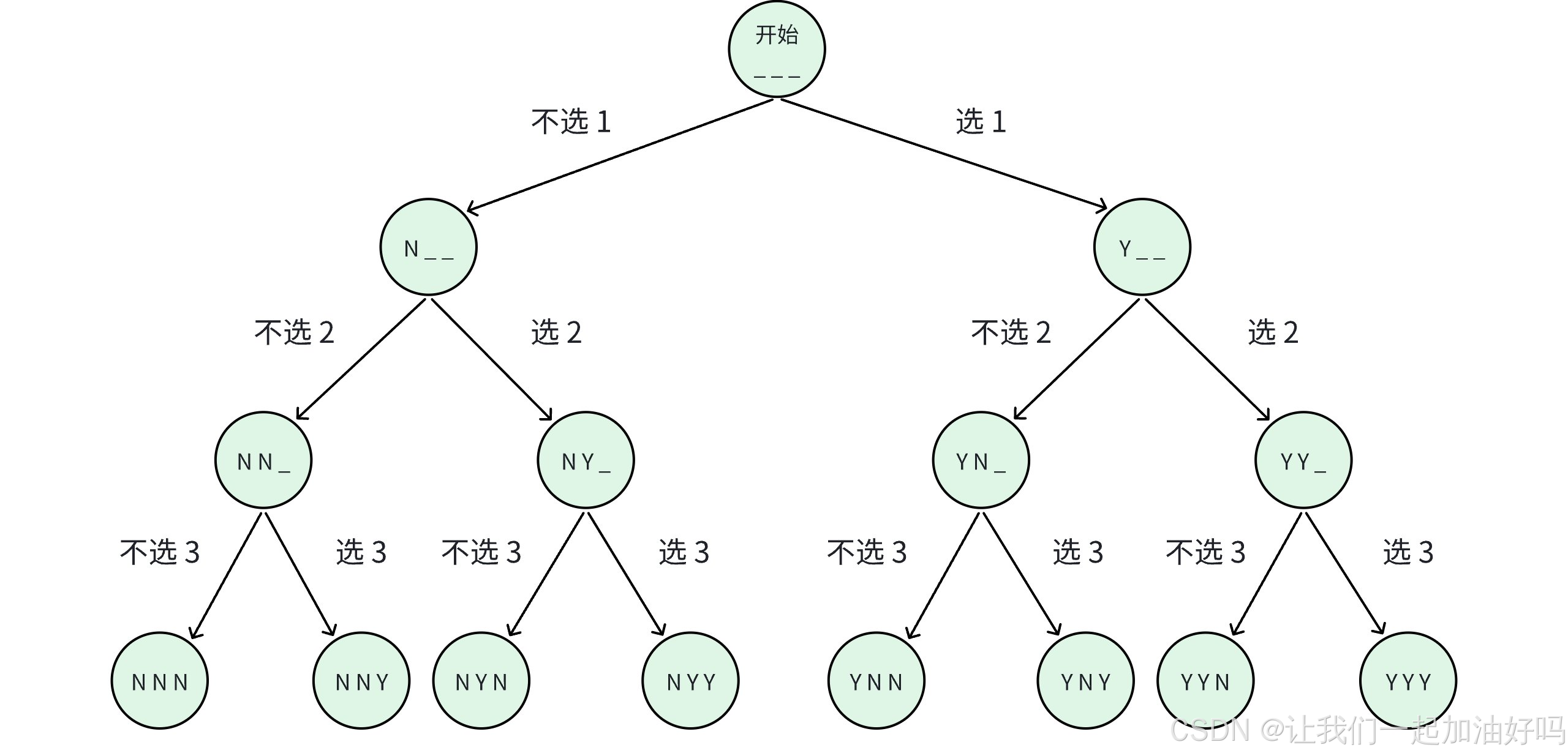
这样的一棵树状图又可以被称为决策树，它能够很好的帮助我们枚举出最后的答案，我们想要获取答案实质上就是对这一棵树进行一次深度优先遍历 (DFS) 。

接下来我们只需要模拟一遍这个决策树的过程即可。怎么模拟？首先，我们肯定是需要用到递归函数的，那么递归函数内部该如何设计？这就要看我们的决策树了。函数体的主体部分就是在模拟决策树的每一层都干了些什么，结束条件就是到叶子节点的时候。

---

(2) 代码实现

#include<iostream>using namespace std;string path;  // 记录递归过程中，每一步的决策
int n;void dfs()
{if(path.size() == n)  // 如果大小为n了说明到叶子节点了，需要输出{cout << path << endl;return;}// 不选path += 'N';dfs();  // 递归到决策树下一层// 到这里就已经重新回到上一层了，这个时候 path 内的最后一个位置还保留了下面层的数据，需要清除掉path.pop_back();  // 回溯，恢复现场// 选path += 'Y';dfs();  // 递归到下一层path.pop_back();  // 回溯，恢复现场
}int main()
{cin >> n;dfs();return 0;
}

---

2. 组合型枚举 ⭐

P10448 组合型枚举 - 洛谷

【题目描述】

从 $1\sim n$ 这 $n$ 个整数中随机选出 $m$ 个，输出所有可能的选择方案。

【输入格式】

两个整数 $n,m$ ,在同一行用空格隔开。

【输出格式】

按照从小到大的顺序输出所有方案，每行 $1$ 个。

首先，同一行内的数升序排列，相邻两个数用一个空格隔开。

其次，对于两个不同的行，对应下标的数一一比较，字典序较小的排在前面（例如 1 3 5 7 排在 1 3 6 8 前面）。

【示例一】

输入

5 3

输出

1 2 3 
1 2 4 
1 2 5 
1 3 4 
1 3 5 
1 4 5 
2 3 4 
2 3 5 
2 4 5 
3 4 5

【说明/提示】

对于所有测试数据满足 $0\le m\le n$ , $ n+(n-m) \le 25 $。

---

(1) 解题思路

首先画出决策树：

注意到在这道题中，由于我们需要枚举的是升序的序列，每一层枚举的时候是从前一个位置数字的下一个数字开始枚举的，因此在 dfs() 函数中，我们需要知道当前层我们应该从哪里开始枚举。

(2) 代码实现

#include<iostream>
#include<vector>using namespace std;vector<int> path;  // 记录递归过程
int n, m;// 从 begin 位置开始往后枚举
void dfs(int begin)
{if(path.size() == m)  // 结束条件{for(auto e : path) cout << e << " ";cout << endl;return;}for(int i = begin; i <= n; i++){path.push_back(i); dfs(i + 1);  // 下一层就从当前位置填的这个数的下一个数开始枚举path.pop_back();  // 恢复现场}
}int main()
{cin >> n >> m;dfs(1);return 0;
}

---

3. 枚举排列 ⭐

【题目链接】

B3623 枚举排列（递归实现排列型枚举） - 洛谷

【题目描述】

今有 $n$ 名学生，要从中选出 $k$ 人排成一列拍照。

请按字典序输出所有可能的排列方式。

【输入格式】

仅一行，两个正整数 $n,k$。

【输出格式】

若干行，每行 $k$ 个正整数，表示一种可能的队伍顺序。

【示例一】

输入

3 2

输出

1 2
1 3
2 1
2 3
3 1
3 2

【说明/提示】

对于 $100\%$ 的数据，$1\le k\le n\le 10$。

---

(1) 解题思路

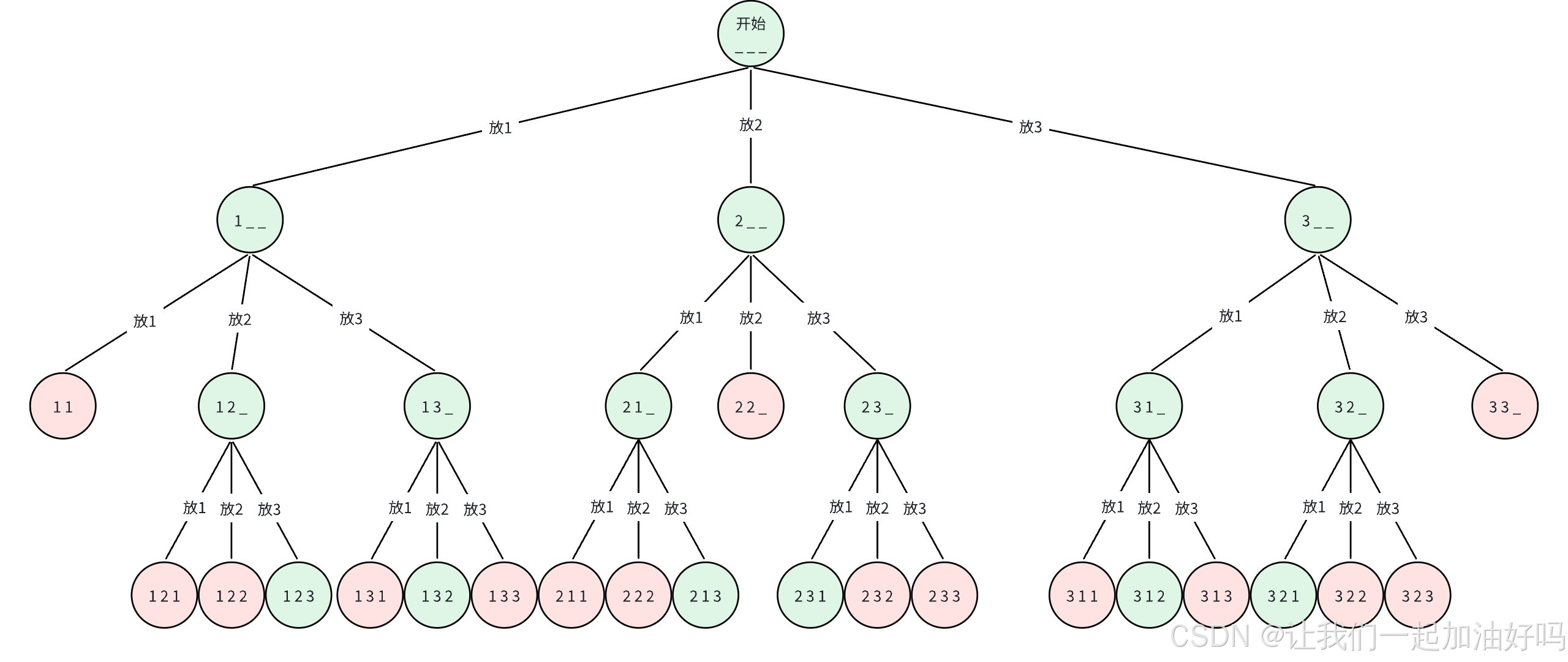
首先画出决策树：

递归函数主体部分的逻辑就是在枚举 1, 2, 3 这三个数，所以我们只需要写一个 for 循环枚举 1 ~ n 即可。重点是我们不能选择已经选过的数字，也就是说我们需要剪枝。如何实现剪枝呢？我们可以搞一个 vis 数组，它的第 i 个位置代表 i 这个数有没有被选择过，在我们枚举的过程中只需要在 vis 数组中看一下当前位置的是否被选择过即可，如果被选择过那么 continue，否则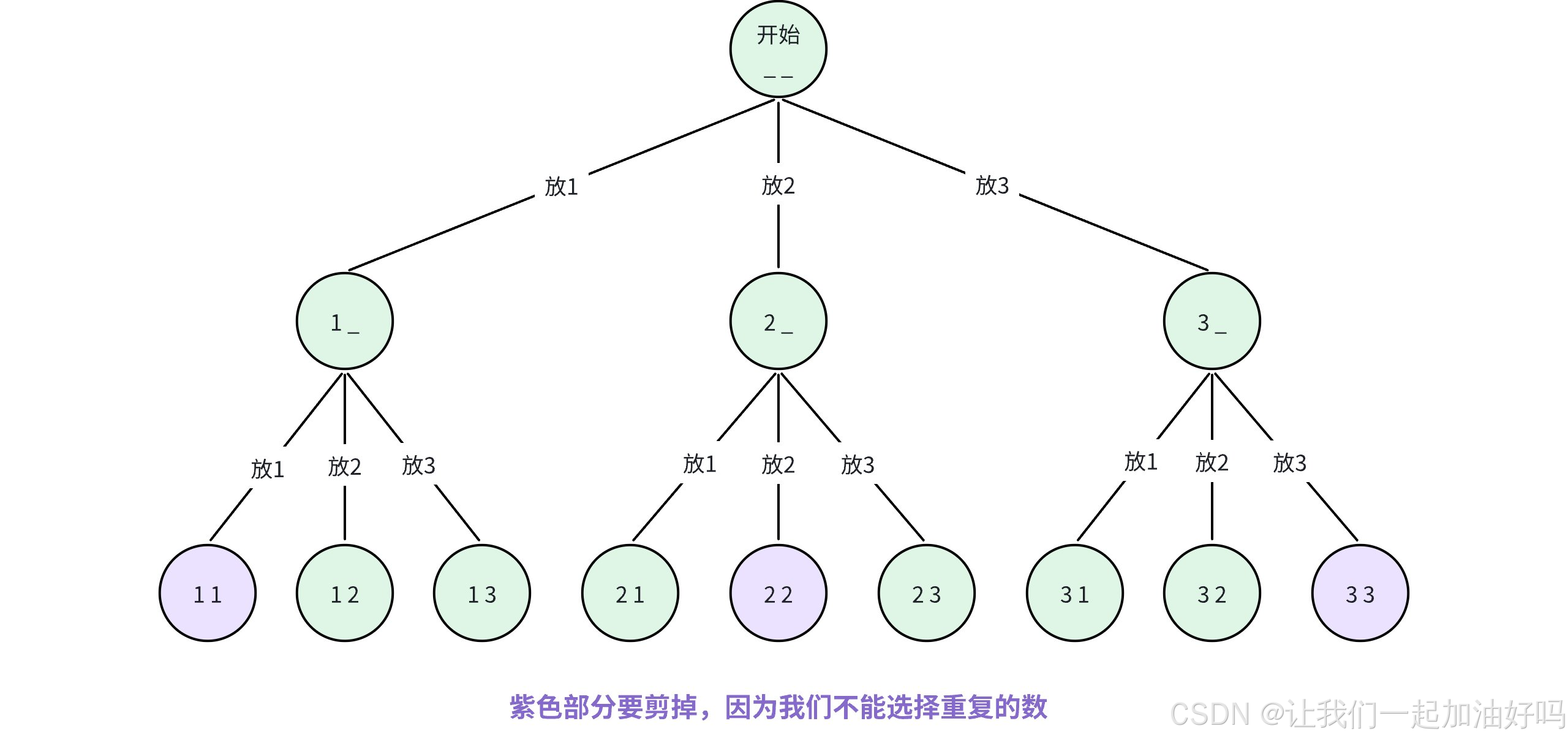
就正常执行。

---

(2) 代码实现

#include<iostream>
#include<vector>using namespace std;const int N = 15;vector<int> path;
bool vis[N];  // 标记哪些数已经被选择了
int n, m;void dfs()
{if(path.size() == m){for(auto e : path) cout << e << " ";cout << endl;return;}for(int i = 1; i <= n; i++){if(!vis[i])  // 如果当前数没有被选择{path.push_back(i);vis[i] = true;  // 当前数被选择了，需要在 vis 数组中标记一下dfs();  // 递归到下一层path.pop_back();  // 恢复现场vis[i] = false;  // 恢复现场}}
}int main()
{cin >> n >> m;dfs();return 0;
}

---

4. 全排列问题 ⭐

【题目链接】

P1706 全排列问题 - 洛谷

【题目描述】

按照字典序输出自然数 $1$ 到 $n$ 所有不重复的排列，即 $n$ 的全排列，要求所产生的任一数字序列中不允许出现重复的数字。

【输入格式】

一个整数 $n$。

【输出格式】

由 $1\sim n$ 组成的所有不重复的数字序列，每行一个序列。

每个数字保留 $5$ 个场宽。

【示例一】

输入

3

输出

	1    2    31    3    22    1    32    3    13    1    23    2    1

【说明/提示】

$1\le n\le 9$。

---

(1) 解题思路

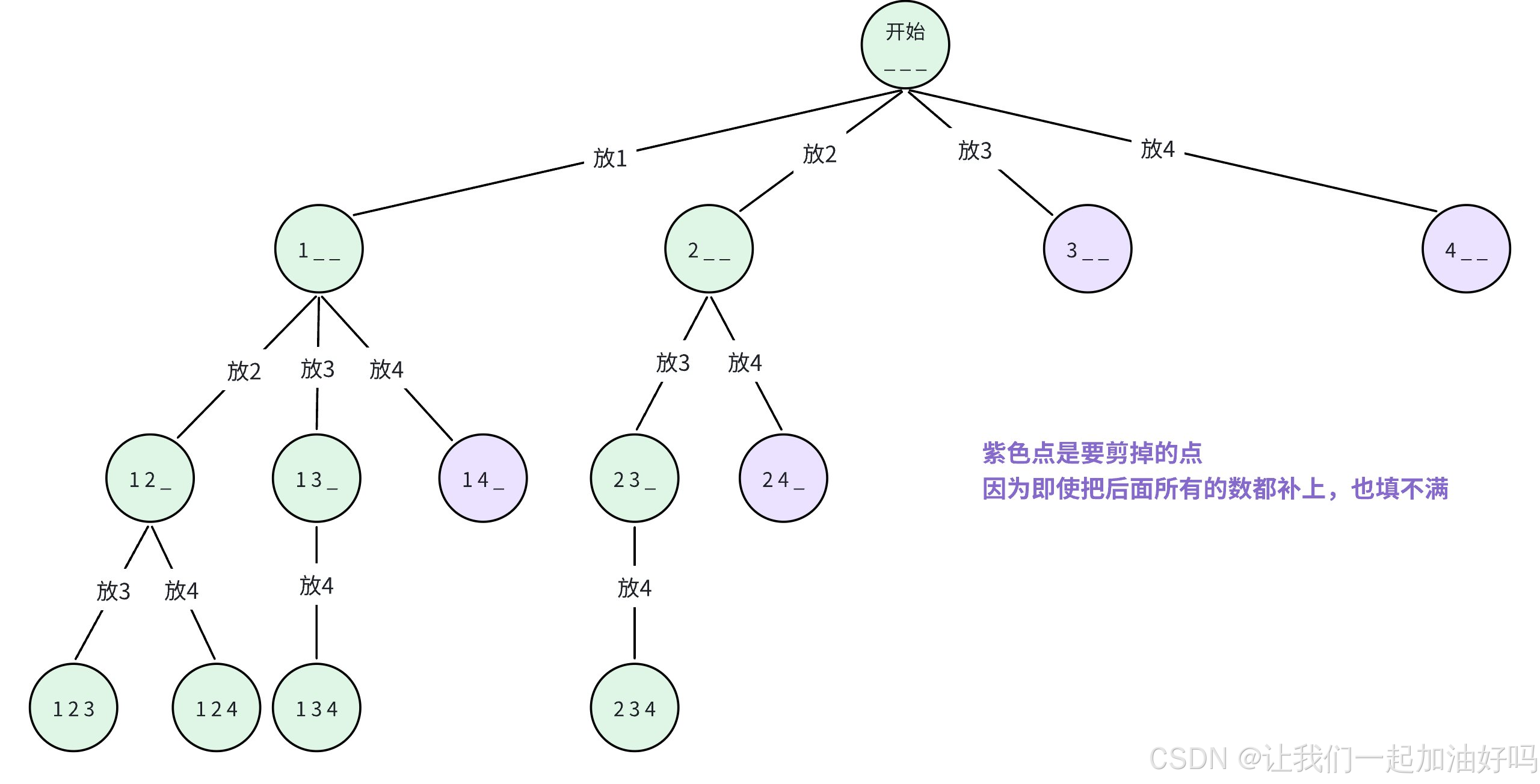
首先画出决策树：

解法同【枚举排列】，唯一不同的是递归出口不同。

---

(2) 代码实现

#include<iostream>
#include<vector>using namespace std;const int N = 10;int n;
vector<int> path;
bool vis[N];void dfs()
{if(path.size() == n){for(auto e : path) cout << "    " << e;cout << endl;return;}for(int i = 1; i <= n; i++){if(!vis[i])  // 如果当前数没有被选择{path.push_back(i);vis[i] = true;dfs();  // 递归到下一层path.pop_back();  // 恢复现场vis[i] = false;  // 恢复现场}}
}int main()
{cin >> n;dfs();return 0;
}