本博客为读《应用密码学》所得笔记

文章目录
- 一、 加密与解密
- 1.2 秘钥Key
- 1.2.1 引入秘钥K
- 1.2.2 加密秘钥K1,解密秘钥K2
- 二、对称算法 VS 公开密钥算法
- **① 对称算法** - 传统密码算法 **(Symmetric Algorithm) 🔑**
- **② 非对称算法特点** - 公开秘钥算法 **(Public-Key Algorithm) 🗝️**
- 密码分析
- 🔬 (1) 正规密码学攻击 (Technical Attacks)
- 😄(2)非正规/社会工程学攻击 (Non-Technical Attacks)
- ✅ 总结与对比
- 三、 代替密码或者换位密码
- 四、了解即可
一、 加密与解密
加密:明文消息需要通过某种方式伪装的过程E(M) = C
被加密后的消息被称为秘文。
解密:由秘文转为明文的过程D(C) = M

密码学还起到 鉴别(抗伪装)、消息完整性、抗抵赖的作用。

1.2 秘钥Key
在密码系统中由算法以及“明文、秘文和秘钥”构成。
✨自此开发者将目光从算法的安全性,转向了对于秘钥守护的安全性的考虑。
1.2.1 引入秘钥K
现代密码学来说,引入秘钥K,K其范围可被称为”秘钥空间“。
✨(为解决受到算法的保密性基于对于算法的一种秘密的现象)

✨ 三个公式
Eₖ(M) = C,Dₖ(C) = M, 和Dₖ(Eₖ(M)) = M之间的逻辑关系。
- 起点 📄 明文 M: 这是需要加密的原始信息。
- 加密过程
Eₖ(M) = C: 使用加密函数 E 和密钥 K,对明文 M 进行运算,得到密文 C。 - 中间状态 🔒 密文 C: 加密后的输出,即
C = Eₖ(M)。 - 解密过程
Dₖ(C) = M: 使用解密函数 D 和相同的密钥 K,对密文 C 进行运算,理论上应还原出明文 M。 - 数学验证
Dₖ(Eₖ(M)) = M: 这是加解密系统核心的正确性条件。将解密后的结果与原始明文 M 进行比对。 - 最终结果:
- 是 ✅ ->
Dₖ(Eₖ(M)) = M成立,意味着 🎉 加解密系统工作正常。 - 否 ❌ -> 等式不成立,意味着过程中出现 🔥 算法或密钥错误。
- 是 ✅ ->
1.2.2 加密秘钥K1,解密秘钥K2
✨ 三个公式
Eₖ₁(M) = C,Dₖ₂(C) = M, 和Dₖ₂(Eₖ₁(M)) = M之间的逻辑关系。
- 起点 📄 明文 M: 这是需要加密的原始信息。
- 加密过程
Eₖ₁(M) = C: 使用加密函数 E 和加密密钥 K₁,对明文 M 进行运算,得到密文 C。 - 中间状态 🔒 密文 C: 加密后的输出,即
C = Eₖ₁(M)。 - 解密过程
Dₖ₂(C) = M: 使用解密函数 D 和解密密钥 K₂,对密文 C 进行运算,还原出明文 M。 - 数学验证
Dₖ₂(Eₖ₁(M)) = M: 这是非对称加密系统的核心正确性条件。使用不同的密钥(K₁ ≠ K₂) 能成功完成加解密循环。 - 最终结果:
- 是 ✅ ->
Dₖ₂(Eₖ₁(M)) = M成立,意味着 🔑 非对称/公钥密码系统工作正常。这正是公钥密码学的特征(例如RSA算法),用一个密钥(公钥)加密,另一个配对但不同的密钥(私钥)解密。 - 否 ❌ -> 等式不成立,意味着 🔥 密钥不匹配或算法错误。
- 是 ✅ ->
二、对称算法 VS 公开密钥算法
① 对称算法 - 传统密码算法 (Symmetric Algorithm) 🔑
- 流程:
数据📄-> (用密钥🔑加密🔒) ->密文📦-> (用同一把密钥🔑解密🔓) ->数据📄 - 核心:加密和解密使用同一把密钥。
- 特点:速度快,效率高,但密钥分发不安全。
- 常见算法:AES, DES, 3DES


✨ 对称算法特点:
**⚡ 高速性能 - 加解密速度快
🔑 单密钥 - 加密解密使用相同密钥
📏 适合大数据 - 处理大量数据效率高
⚠️ 密钥分发挑战 - 需要安全共享密钥
② 非对称算法特点 - 公开秘钥算法 (Public-Key Algorithm) 🗝️
- 流程:
数据📄-> (用接收者的公钥🌐加密🔒) ->密文📦-> (用接收者的私钥🛡️解密🔓) ->数据📄 - 核心:使用一对密钥:公钥(公开)和私钥(自己保留)。
- 特点:速度慢,但解决了密钥分发问题,用于数字签名、密钥交换等。
- 常见算法:RSA, ECC, ElGamal
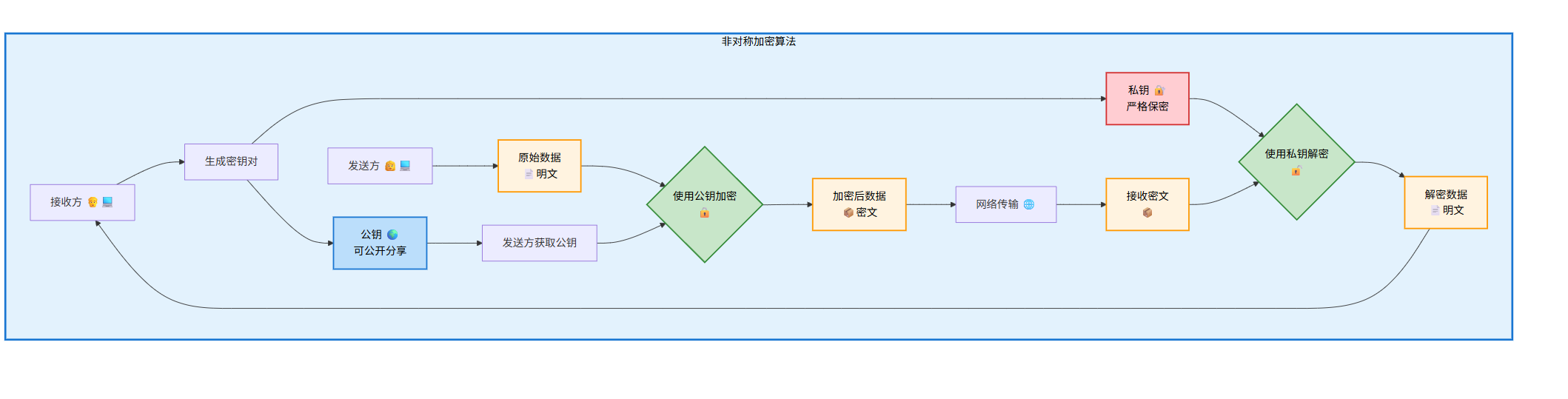
✨ 非对称算法特点:
🛡️ 双重密钥 - 公钥加密,私钥解密
🌍 公钥共享 - 公钥可以自由分发
🔐 私钥保护 - 私钥必须严格保密
🐢 速度较慢 - 适合小数据量加密
✅ 解决密钥分发 - 无需预先共享密钥
密码分析
密码编码学的目的:防止偷听者知晓发送方和接收方之间的通讯信息。
密码分析学的目的:未知秘钥的情况下,恢复明文的科学方式。(此时也就是恢复明文和对应秘钥)
秘钥通过非密码分析得来行为称为泄露
分析阶段的一列尝试称为:攻击(attack)
下面展示常见的方式

🔬 (1) 正规密码学攻击 (Technical Attacks)
这些是教科书和学术论文中严格定义的攻击模型。
| 攻击方式 | 正式英文名 | 原理 | 比喻 |
|---|---|---|---|
| 唯密文攻击 | Ciphertext-Only Attack | 最基础的攻击。分析者只有一段或几段密文,没有其他信息。难度最大。 | 只听到一段加密的外语,试图理解它。 |
| 已知明文攻击 | Known-Plaintext Attack (KPA) | 分析者拥有一些密文,以及这些密文对应的明文。目标是破解密钥或其他密文。 | 拿到一张“密码本”的一页,试图破解整个密码本。 |
| 选择明文攻击 | Chosen-Plaintext Attack (CPA) | 分析者可以选择任意明文,并获取其对应的密文。这是现代加密算法必须抵御的攻击。 | 可以让翻译官把你说的任何话都翻译成那种外语,你通过对比来学习规则。 |
| 自适应选择明文攻击 | Adaptive CPA | CPA的强化版。分析者可以基于之前加密的结果,动态地选择下一个要加密的明文。更接近现实攻击。 | 不仅能让翻译官翻译,还能根据上一句的翻译结果,机智地问下一句。 |
| 选择密文攻击 | Chosen-Ciphertext Attack (CCA) | 分析者可以选择任意密文,并获取其解密后的明文。目标是破解密钥。 | 可以让翻译官把任何你提供的“密文”翻译回明文,从而找出规则。 |
| 选择密钥攻击 | Chosen-Key Attack | 分析者对密钥之间的关系有一定的了解或选择能力。这种攻击更理论化,主要用于分析加密算法的某些数学属性。 | 你知道两把钥匙之间有某种联系,试图利用这种联系。 |
😄(2)非正规/社会工程学攻击 (Non-Technical Attacks)
这些不是密码学意义上的数学分析,而是通过“人”的弱点来获取密钥的非常规手段,通常被称为 “旁路攻击” 或 “社会工程学攻击”。
| 攻击方式 | “黑话”英文名 | 原理 | 比喻 |
|---|---|---|---|
| 软磨硬泡攻击 | Rubber-Hose Cryptanalysis | 通过威胁、勒索或暴力手段(比如用橡胶水管抽打)逼迫密钥持有者交出密钥。 | 不是破解保险箱,而是用枪指着保险箱的主人让他打开。 |
| 购买密钥攻击 | Purchase-Key Attack | 通过贿赂或直接购买的方式从内部人员或意志不坚定的持有者那里获得密钥。 | 直接花钱从保安那里买钥匙。 |
✅ 总结与对比
**安全性顺序:**全部破译 > 全盘推导 > 实例(局部)推导 > 信息推导
复杂性包含: 数据载入量 、 工作因素(处理复杂度)、存储
| 特性 | 正规密码学攻击 | 非正规社会工程学攻击 |
|---|---|---|
| 目标 | 算法本身的数学缺陷 | 人的弱点(恐惧、贪婪、疏忽) |
| 方式 | 数学分析、计算 | 威胁、贿赂、欺骗 |
| 防御 | 使用更强加密算法 | 加强法律、管理、培训、物理安全 |
一个安全的系统,必须同时能够抵御技术上的密码攻击和现实中的软磨硬泡攻击。
三、 代替密码或者换位密码
在我们日常使用图像中不难发现图像具有多种包含了多种信息。
例如我们有8位的灰度图,我们仅需“128 X 128"图像中每一个像素的最后1位,整体替换后就达成了实现“图像水印”的效果,虽然在肉眼上可能和原图近乎无差别,但是我们分解开其没一位的话,还是可以看见水印标志出制作者独特的标记的。
- 代替密码
明文中的每一个字符被替换成秘文中的每一个字符,当接受者对秘文进行逆运算将恢复出明文。
经典密码学中:简单替换、多名码代提、多字母替代、多表替代。
- 换位密码

- 转轮机
四、了解即可
- 异或XOR操作
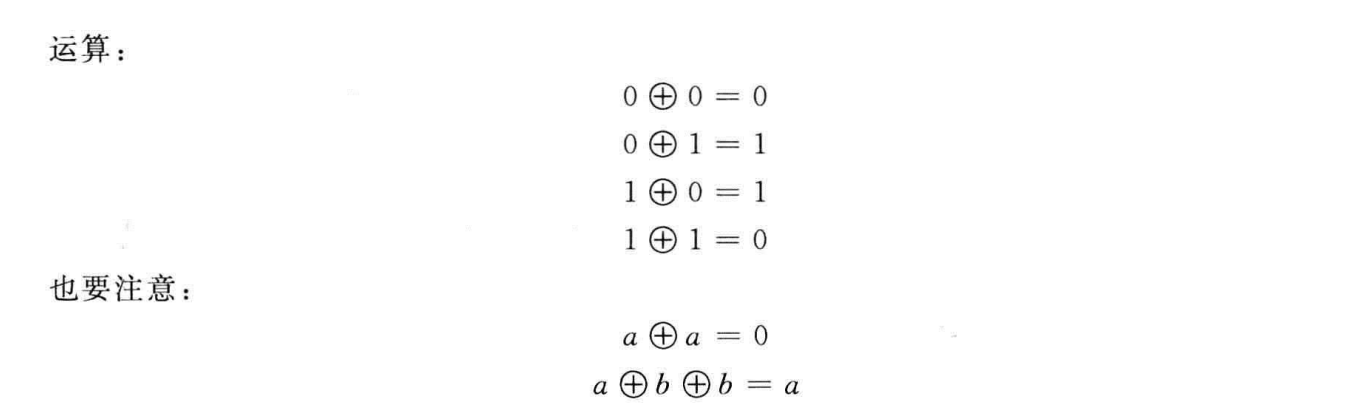
-
一次一密:
用一把只能用一次的、完全随机生成的、和明文一样长的“钥匙”来加密。只要做到这三点,它在数学上就是“无法破解”的。
-
计算机算法
- 数据加密算法(DES):对称算法
- RSA:用作加密和数字签名
- 数字签名算法(DSA):不可在加密中运用









初步)
)






:如何通过Federated实现跨实例访问表)


