文章目录
- 73.矩阵置零
- 题目:
- 思路:
- 方法一:用两个标记数组(易理解,额外空间 O(m+n))
- 思路(直观)
- 举例([[1,1,1],[1,0,1],[1,1,1]])
- 优缺点
- 代码实现(Go)
- 方法二:用第一行与第一列做标记(原地,额外空间 O(1))
- 思路
- 步骤
- 代码实现(Go)
- 总结比较
73.矩阵置零
题目:
给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。
示例 1:
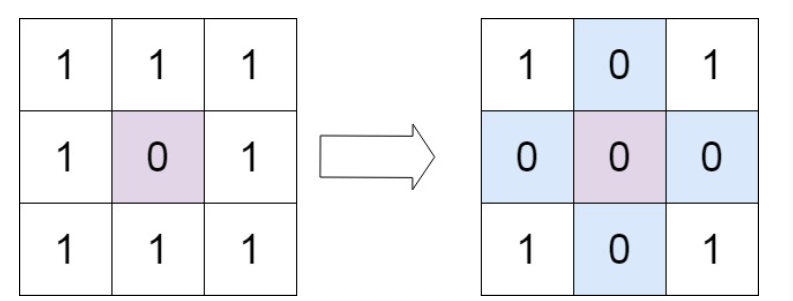
输入:matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出:[[1,0,1],[0,0,0],[1,0,1]]
示例 2:
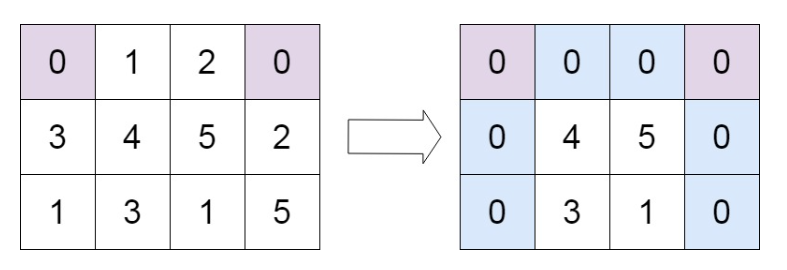
输入:matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出:[[0,0,0,0],[0,4,5,0],[0,3,1,0]]
提示:
m == matrix.length
n == matrix[0].length
1 <= m, n <= 200
-2^31 <= matrix[i][j] <= 2^31 - 1
思路:
方法一:用两个标记数组(易理解,额外空间 O(m+n))
思路(直观)
- 新建两个布尔数组
row[m]和col[n],初始都为false。 - 第一次遍历整个矩阵:如果
matrix[i][j] == 0,就设row[i] = true,col[j] = true。 - 第二次遍历整个矩阵:如果
row[i] || col[j]为true,就把matrix[i][j] = 0。
举例([[1,1,1],[1,0,1],[1,1,1]])
- 第一次扫描后:
row = [false, true, false],col = [false, true, false] - 第二次把第 1 行和第 1 列(索引从 0 开始)按标记置为 0,得到结果
[[1,0,1],[0,0,0],[1,0,1]]。
优缺点
- 优点:实现简单、直观、易于验证。
- 缺点:额外空间 O(m + n)。
代码实现(Go)
详细注解:
// package main// import "fmt"func setZeroes(matrix [][]int) {m, n := len(matrix), len(matrix[0])// 标记数组(一维布尔数组):记录每一行是否需要置零row := make([]bool, m)// 标记数组(一维布尔数组):记录每一列是否需要置零col := make([]bool, n)// 第一次遍历:找到所有为 0 的位置for i := 0; i < m; i++ {for j := 0; j < n; j++ {if matrix[i][j] == 0 {row[i] = true // 这一行需要清零col[j] = true // 这一列需要清零}}}// 第二次遍历:根据标记数组更新矩阵for i := 0; i < m; i++ {for j := 0; j < n; j++ {if row[i] || col[j] {matrix[i][j] = 0}}}
}// func main() {
// m1 := [][]int{{1, 1, 1}, {1, 0, 1}, {1, 1, 1}}
// setZeroes(m1)
// fmt.Println(m1) // 输出[[1 0 1] [0 0 0] [1 0 1]]
// }方法二:用第一行与第一列做标记(原地,额外空间 O(1))
思路
把 row 和 col 两个标记数组“挪到”矩阵的第一行和第一列去存储,这样不需要额外数组。但第一行/第一列本身可能一开始就包含 0,若直接当标记使用会丢失它们原本是否含 0 的信息。
因此需要额外两个布尔变量 row0 和 col0 保存第一行和第一列初始是否包含 0。其余步骤和方法一等价(先标记,再根据标记清零),只是标记位置换成了矩阵本身。
步骤
- 先扫描第一行,设置
row0 = true如果第一行含 0。 - 先扫描第一列,设置
col0 = true如果第一列含 0。
(这两步必须在修改 matrix[0][* ] 或 matrix[*][0] 之前完成,否则会丢信息。) - 对
i=1..m-1, j=1..n-1扫描:若matrix[i][j] == 0,则置matrix[i][0] = 0(标记第 i 行),matrix[0][j] = 0(标记第 j 列)。 - 根据第一列的标记清零那些整行(i >= 1)。
- 根据第一行的标记清零那些整列(j >= 1)。
- 最后根据
row0和col0决定是否把首行/首列全清 0。
注意细节:在第 4、5 步 要跳过第一列/第一行的标记位本身(即从索引 1 开始),防止干扰标记区。最后一步再处理首行/首列。
代码实现(Go)
详细注解:
// package main// import "fmt"func setZeroes(matrix [][]int) {m, n := len(matrix), len(matrix[0])// 两个变量单独记录第一行和第一列是否需要清零row0 := falsecol0 := false// 1) 先检查第一列是否需要清零for i := 0; i < m; i++ {if matrix[i][0] == 0 {col0 = truebreak}}// 2) 再检查第一行是否需要清零for j := 0; j < n; j++ {if matrix[0][j] == 0 {row0 = truebreak}}// 3) 用第一行和第一列作为标记// 从 (1,1) 开始遍历(不动第一行第一列),// 如果 matrix[i][j] == 0,就标记 matrix[i][0] 和 matrix[0][j] 为 0for i := 1; i < m; i++ {for j := 1; j < n; j++ {if matrix[i][j] == 0 {matrix[i][0] = 0 // 标记这一行matrix[0][j] = 0 // 标记这一列}}}// 4) 再次遍历 (1,1) 开始的子矩阵// 逐个遍历矩阵内部元素,根据第一行和第一列的标记,只要行或列被标记,就把该位置置零for i := 1; i < m; i++ {for j := 1; j < n; j++ {if matrix[i][0] == 0 || matrix[0][j] == 0 {matrix[i][j] = 0}}}// 5) 最后处理第一列:如果第一列有 0,就需要把第一列整列置零if col0 {for i := 0; i < m; i++ {matrix[i][0] = 0}}// 以及第一行,如果第一行有 0,就需要把第一行整行置零if row0 {for j := 0; j < n; j++ {matrix[0][j] = 0}}
}// func main() {
// m1 := [][]int{{1, 1, 1}, {1, 0, 1}, {1, 1, 1}}
// setZeroes(m1)
// fmt.Println(m1) // 输出[[1 0 1] [0 0 0] [1 0 1]]
// }无注释:
// package main// import "fmt"func setZeroes(matrix [][]int) {m, n := len(matrix), len(matrix[0])row0 := falsecol0 := falsefor i := 0; i < m; i++ {if matrix[i][0] == 0 {col0 = truebreak}}for j := 0; j < n; j++ {if matrix[0][j] == 0 {row0 = truebreak}}for i := 1; i < m; i++ {for j := 1; j < n; j++ {if matrix[i][j] == 0 {matrix[i][0] = 0matrix[0][j] = 0}}}for i := 1; i < m; i++ {for j := 1; j < n; j++ {if matrix[i][0] == 0 || matrix[0][j] == 0 {matrix[i][j] = 0}}}if col0 {for i := 0; i < m; i++ {matrix[i][0] = 0}}if row0 {for j := 0; j < n; j++ {matrix[0][j] = 0}}
}// func main() {
// m1 := [][]int{{1, 1, 1}, {1, 0, 1}, {1, 1, 1}}
// setZeroes(m1)
// fmt.Println(m1) // 输出[[1 0 1] [0 0 0] [1 0 1]]
// }总结比较
| 特性 | 方法一(标记数组) | 方法二(首行首列做标记) |
|---|---|---|
| 额外空间 | O(m + n) | O(1) |
| 实现难度 | 简单 | 稍复杂(要注意首行/首列) |
| 面试倾向 | 如果不限空间,用它写起来安全 | 通常面试官更喜欢 O(1) 的聪明解法(方法二) |

)


)









)


![[系统架构设计师]知识产权(二十)](http://pic.xiahunao.cn/[系统架构设计师]知识产权(二十))

