无懈可击的 TCP AIMD

不特指 TCP AIMD，而泛指控制范畴的所有 Additive Increase / Multiplicative Decrease 算法，继难以超越的 TCP AIMD 再叙。

“你永远不能仅凭 BBR 的吞吐更高就说 BBR 比 CUBIC 更好” 这句话怎么总是没人看，这句话是这一系列文章的前提论点，但却总有人看了全文后用 “BBR 性能更高” 来表明自己见多识广。

再次给出 AIMD 算法吞吐率 T 和丢包率 p 以及 RTT 关系的公式：

$T=γRTT⋅p−0.5T=\dfrac{\gamma}{\text{RTT}}\cdot p^{-0.5}$

在三维坐标系里画图，结论就是：

AIMD 算法受 RTT 影响巨大，RTT 越大，吞吐越低；
AIMD 算法受丢包率 p 影响巨大，p 越大，吞吐越低；

如来自 IBM Aspera 的广告图描述上述正合适：
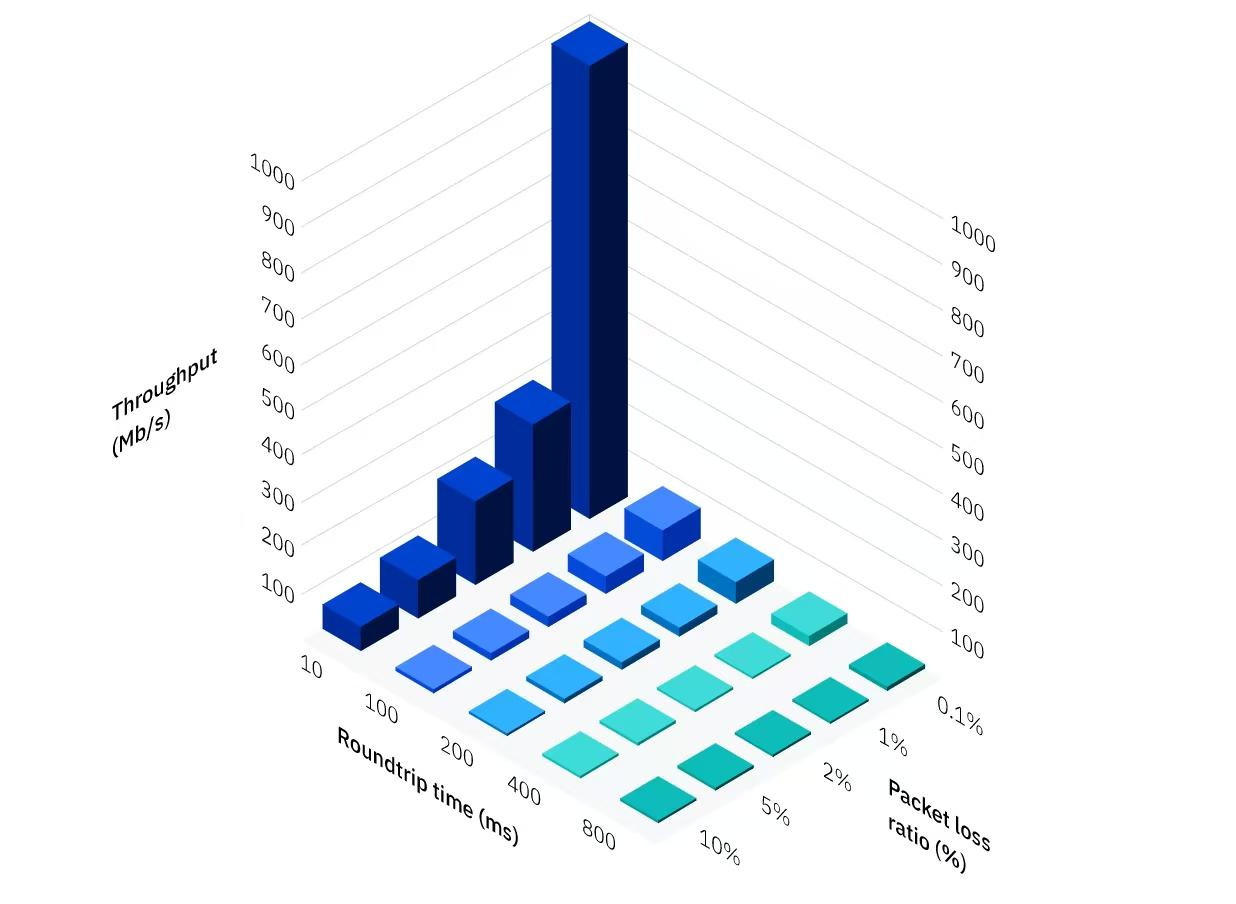
在这里插入图片描述

还有个推论：

端到端传输控制是 “and” 关系，丢包与路径长度正相关，往往 RTT 越大，p 也越大；

这些即 “长肥管道中 TCP 窗口张开难的故有问题” 的量化描述，长肥管道问题历经 30 年，终于在 2010 年代不能再无视，必须解决，原因在于 “依照 AIMD 公式，高速 TCP 需要控制 p 在某个值 Q 之下，而大多数传输介质的固有丢包率都在 Q 之上”，换句话说，介质由于固有丢包率太高而无法满足高速 TCP 的要求。

如何解决长肥管道的问题，还得从本质入手。

这明明是介质不中用了，关 AIMD 公式什么事。引力距离超过洛希极限掌控不了了，就是牛顿错了？介质不中用了就优化介质，介质电气特性本身就有定义了传输吞吐极限的含义，比如所谓五类，超五类双绞线，目前面对超高速 TCP 而言，只是没有哪种介质对应 400Gbps 传输带宽而已，而不是 AIMD 算法不好。

相反，综合考虑成本，带宽利用率，公平性等，AIMD 是综合效能最好的算法，没有之一，AIMD 恰如其分适应尽力而为的网络。参考难以超越的 TCP AIMD。

AIMD 公式的正则推导不难，我的总结看这里：

AIMD 公式的一般推导(附几何推导引用)
TCP AIMD 公式的推导

更正式的论文参考 The Macroscopic Behavior of the TCP Congestion Avoidance Algorithm。

但这次我们用更加直观的方式重新审视 AIMD 公式，-0.5 次幂值得注意，这意味着 p 和 W 的平方存在反比关系，这个平方如何理解。按照生灭守恒，MD 视作丢包惩罚，AI 视作奖励，则：

$(惩罚量)⋅(惩罚概率)∝(奖励量)⋅(奖励概率)(惩罚量)\cdot (惩罚概率) \propto (奖励量)\cdot(奖励概率)$

AIMD 的惩罚量为 β·W，惩罚概率即丢包率 p，奖励量为 1，奖励概率即每个 RTT 一次，即 $RWR=1W\dfrac{\frac{R}{W}}{R}=\dfrac{1}{W}$ ，总体上就是：
$β⋅W⋅p∝1⋅1W\beta\cdot W\cdot p \propto 1\cdot\dfrac{1}{W}$

至于为什么如此，直观上即可理解。

以吹气球为例，气球的破裂容量决定了两个维度的度量，一个是气球的最大容量，另一个是把气球吹到最大容量的时间，而 AIMD 的过程非常像吹气球，buffer 满了丢包视为气球吹爆，它决定了丢包时的最大窗口 W 以及到达最大窗口的时间 0.5·W·RTT，因此 $W2∝1pW^2 \propto \frac{1}{p}$ ，剩下的就是待定系数了。

用吹气球的过程套用生灭守恒，则气球爆裂瞬间释放 W 气体，吹爆气球的频率为 p，按照 AIMD 将气球吹起来需要 W 口气，则吹气频率即 $1W\dfrac{1}{W}$ ，那么 $W⋅p=1⋅1WW\cdot p=1\cdot\dfrac{1}{W}$ ，还是一样的结论。

考虑一个有 n +1 个气孔的气球，其中 1 个气孔出气，n 个气孔进气，如果我们要求气球内部必须保留一定气体从出气孔持续放出，考虑 n 人一起从 n 个进气孔吹同一个气球的场景。如果 n = 1，为了照顾人有限的肺活量，气球容量必须至少等于人的最大肺活量，且吹得太快容易爆裂，吹得太慢换气时出气孔没气体，但 n = 3 时，一个人换气时，另外 2 人可能依然保持吹气，就这样让 n 不断增大。

随 n 不断增大，单个人的换气行为导致的气体波动被稀释了。流越多，所需 buffer 越小，但带宽利用率仍然很高，这就是网络对 buffer 需求的平方反比律，参见交换机 buffer 的平方反比律。

流越多，峰越容易被平滑到谷，总体方差越小，大数中心极限定理，整体越收敛，这就是统计的力量，勾勒出的是现实的美感。

因此 AIMD 算法对 buffer 的需求是向内敛的，不会膨胀，这意味着 AIMD 算法具有良好的扩展性。从这个论点再次看出，AIMD 只需要非常小的代价便可以保持网络在整体上公平高效的可用性，且随着流增多，buffer 需求却不增反降，抖动也被平滑，时延亦具有扩展性。这一切竟然都是自动的，只要执行最简洁的 AIMD。

维持互联网公平高效可用的根基竟然就是多人吹气球。

在这个和谐的场景，单独侵入一条 BBR 流，然后说 BBR 可以获得更大的吞吐，从而证明 BBR 比 AIMD 更优，这是当前绝大多数人的观点，我早已抛弃了这个观点，经历了满怀激情的无果优化，深入理解了 TCP/IP 尽力而为的本质后，我明白了 AIMD 少就是多。

现在开始考虑更加现实的情况。

网络是一个开放系统而非封闭系统，这意味着网络状态时刻随输入，输出，反馈而改变，正如股票，有人买它就会涨，有人卖它就会跌，让你永远捉摸不定它的下一步走势，因为这个走势直接由买卖者自己的行为决定。同样， AIMD 公式需要修正，修正的重点在于，p 在 “多大程度” 上决定 AIMD 周期和最大窗口，这个程序是非线性的，因此需要重新建模：

$T=γRTProp⋅p−αT=\dfrac{\gamma}{\text{RTProp}}\cdot p^{-\alpha}$ ，其中 $0<α≤10<\alpha\le 1$

以上更加实际的模型显然无法通过理论推导计算出来参数，接下来就是在每一个特定场景用海量测量数据喂这个模型，求出该场景下最佳拟合结果的 α，β。区别就在于 “理论计算” 还是 “经验总结”。
该模型可以精确预测一个开发中的系统最终的预期理论吞吐，比如用各种 p 得到的实际结果求出 α，β 后，就可以根据系统的结构蕴含的 p 求出 T。它比理论上的 -0.5 次幂以及各种不同 AIMD 算法理论上的 β 更具有实际意义。

以下是这件事和这场论述的缘起，我先给出我的一个拟合模型：

$T=1.05⋅MSSRTT⋅p−0.75T=1.05\cdot\dfrac{\text{MSS}}{\text{RTT}}\cdot p^{-0.75}$

我的 tun/tap 背靠背转发程序里设置了 40MB buffer，在处理 RingBuffer 边界回绕时没处理好，意味着每 40MB 数据丢一个 MSS，测下来只有 490Mbps，fix bug 前需要一个期望，我的期望是跑满千兆，依据就是以上公式。该模型的参数基于 cubic 精确拟合过，至于 40MB 还是 5MB，也可反算，最终得到最佳解。

将 p 视作通用损耗率，该模型几乎适合任何系统求解最佳吞吐。

该总结一下了，形而上时间。

AIMD 公式虽简洁，但与性能挂钩就很不好看，吞吐随 p 衰减太厉害。人们总觉得有 “巨大优化空间”，总想着去 “优化” 它，BBR 出来了，吞吐上来了，但付出了更大的公平性和测量的代价，代码越搞越复杂。问题是如何定义 “更优”，值得编程者注意的是，网络是一个开放非线性系统，而非线性系统的问题不仅仅关乎计算机技术，遗憾的是，BBR 出自计算机技术学科内线性的假设。

如果快速衰减就是不可违抗的自然律呢，而自然本就是典型的非线性系统，这种函数随自变量非线性变化的自然律太正常了。观测被编程者膜拜的无敌香农公式，设信号为 1，噪声为 p，信道容量为

$C=B⋅log⁡2(1+1p)C=B\cdot\log_2(1+\dfrac{1}{p})$

与 AIMD 几乎一致，二者均显示非线性衰减特征：
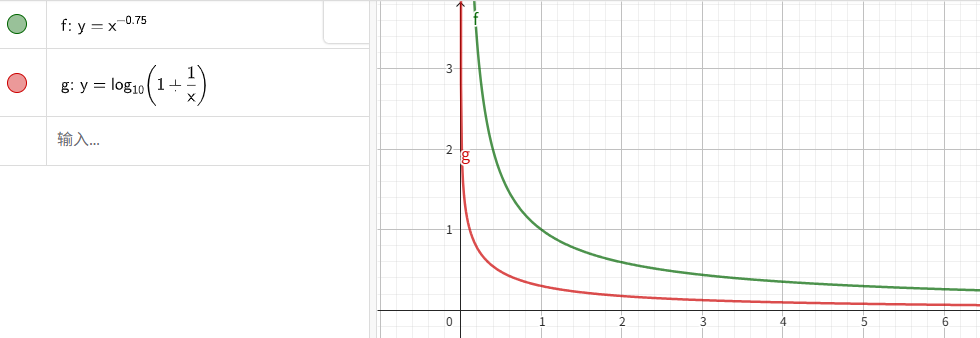
在这里插入图片描述

噪声增加一点点，信道容量下降很多。

类似的，材料疲劳寿命和应力波动，金融投资收益与风险，生态学种群增长与流行病，均描述了相似的非线性特征。

这并非意味着这些公式描述的衰减存在优化空间，恰恰相反，这说明这些公式描述的世界本质上就是这样的，这是真实世界中真实的衰减，无法抗拒的衰减。而真实世界符合最小作用量，这意味着它们已经是最优解。

回到 AIMD，它是一种极其自然的作用力，自然作用力天然具有公平性特征，其不变量就是时间在共享 buffer 里的弹性，一条流的 buffer 排队时间多了，该作用力会更强烈让其排出更多。

为什么收敛行为这么简洁和优雅？只因为它是自然的，多一点都是多。

更直观的例子是非牛顿流体，不管形状如何，只要质量相同，在重力的作用下，它们最终肯定占据相同的占地面积，因为重心高了，重力会拉低它，将高度补偿给面积后，拉低的力度逐渐变弱，最终大家一致，就好像大家刚挤上一辆公交车时气都喘不过来，车开了点播一段时间后，就逐渐宽松且公平了， $RTT=InfltBW\text{RTT}=\dfrac{\text{Inflt}}{\text{BW}}$ 表达的也是一个意思。