模型创新性
在国赛数学建模中,完备性是论文的基本要求,而创新性则是决定论文能否脱颖而出的关键因素。所谓创新,并不仅仅指提出完全新颖的数学理论,而是能够在已有方法的基础上,通过新的问题切入点、假设修正、模型优化或求解改进,使模型更契合实际问题、更具解释力与推广价值。模型创新性主要体现在以下几个方面:
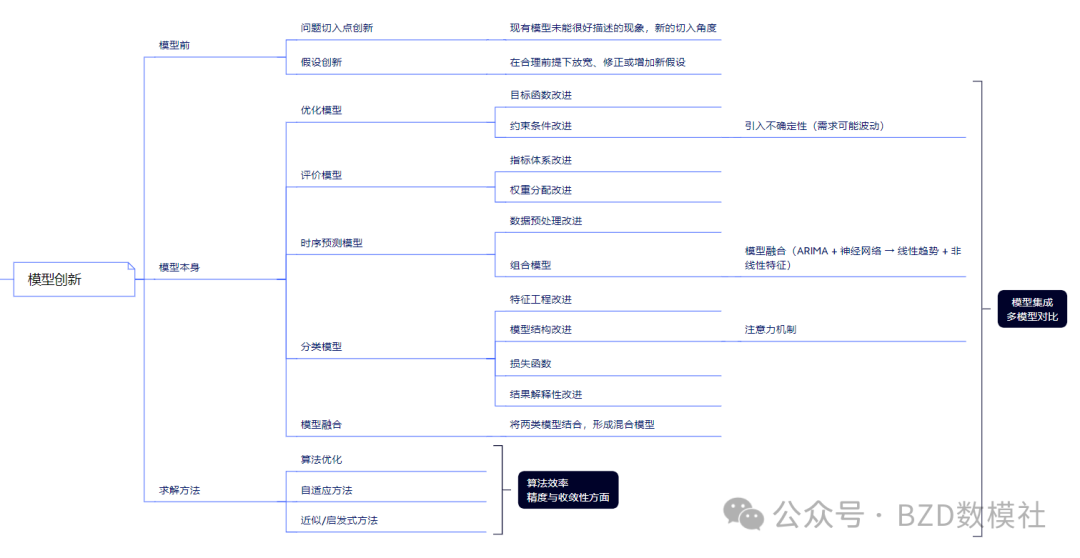
1. 模型前的创新
在建模初始阶段,可以通过新的切入点或假设来展现创新思维。
问题切入点创新:针对现有模型无法很好描述的现象,提出新的建模角度。例如,从个体行为出发,而非宏观总量,建立更具解释力的微观模型。
假设创新:在合理前提下,对传统假设进行放宽、修正或补充。例如,在资源分配问题中引入不完全信息假设,或在预测问题中允许外部环境扰动的存在。
2. 模型本身的创新
模型结构与功能的改进,是创新性的核心体现。
优化模型:在目标函数中引入多目标权衡或动态约束;在约束条件中考虑不确定性因素(如需求波动、价格随机性)。
评价模型:改进指标体系或权重分配方式,使评价更科学合理;例如采用熵权法、层次分析法等改进传统平均权重。
时序预测模型:在数据预处理阶段引入新方法(如小波分解、滑动窗口),或通过模型融合(如 ARIMA 与神经网络结合)同时捕捉线性趋势与非线性特征。
分类模型:在特征工程中构造新特征;在模型结构上引入注意力机制或残差连接;在损失函数设计中考虑类别不均衡;同时提升模型结果的可解释性。
模型融合:将不同类型模型结合,形成混合建模框架。例如,将基于机理的物理模型与基于数据的机器学习模型相结合,提升预测精度与适用范围。
3. 求解方法的创新
在求解过程中对算法进行改进,同样是论文加分点。
算法优化:改进传统优化方法的收敛速度与精度。
自适应方法:让算法参数根据数据特征自动调整,例如自适应学习率方法。
近似/启发式方法:在复杂模型难以精确求解时,采用启发式或元启发式算法(如遗传算法、模拟退火、粒子群优化)寻找近似最优解,提高计算效率与可行性。





)
:HandlerExceptionResolver - 异常处理的艺术)
介绍)



第一轮题解)




)


