lc1668
不能直接跳
class Solution {
public:
int maxRepeating(string sequence, string word) {
int k = 0, n = sequence.size(), wn = word.size(), t = 0;
for (int i = 0; i <= n - wn; i++) {
if (sequence.substr(i, wn) == word) {
t = 1;
int j = i + wn;
while (j + wn <= n && sequence.substr(j, wn) == word) {
t++;
j += wn;
}
k = max(k, t);
}
}
return k;
}
};
lc969
两次翻转实现煎饼排序:先找到当前未排序部分的最大元素
第一次翻转将其移到数组开头
第二次翻转将其移到当前未排序部分的末尾(即正确位置)
重复此过程直到数组有序,最终返回所有翻转操作的长度记录。

class Solution {
public:
vector<int> pancakeSort(vector<int>& a)
{
int n=a.size();
vector<int> res;
for(int i=n;i>1;--i){
int m=-1,idx=-1;
for(int j=0;j<i;++j)
{
if(a[j]>m)m=a[j],idx=j;
}
reverse(a.begin(),a.begin()+idx+1);
reverse(a.begin(),a.begin()+i);
res.push_back(idx+1);
res.push_back(i);
}
return res;
}
};

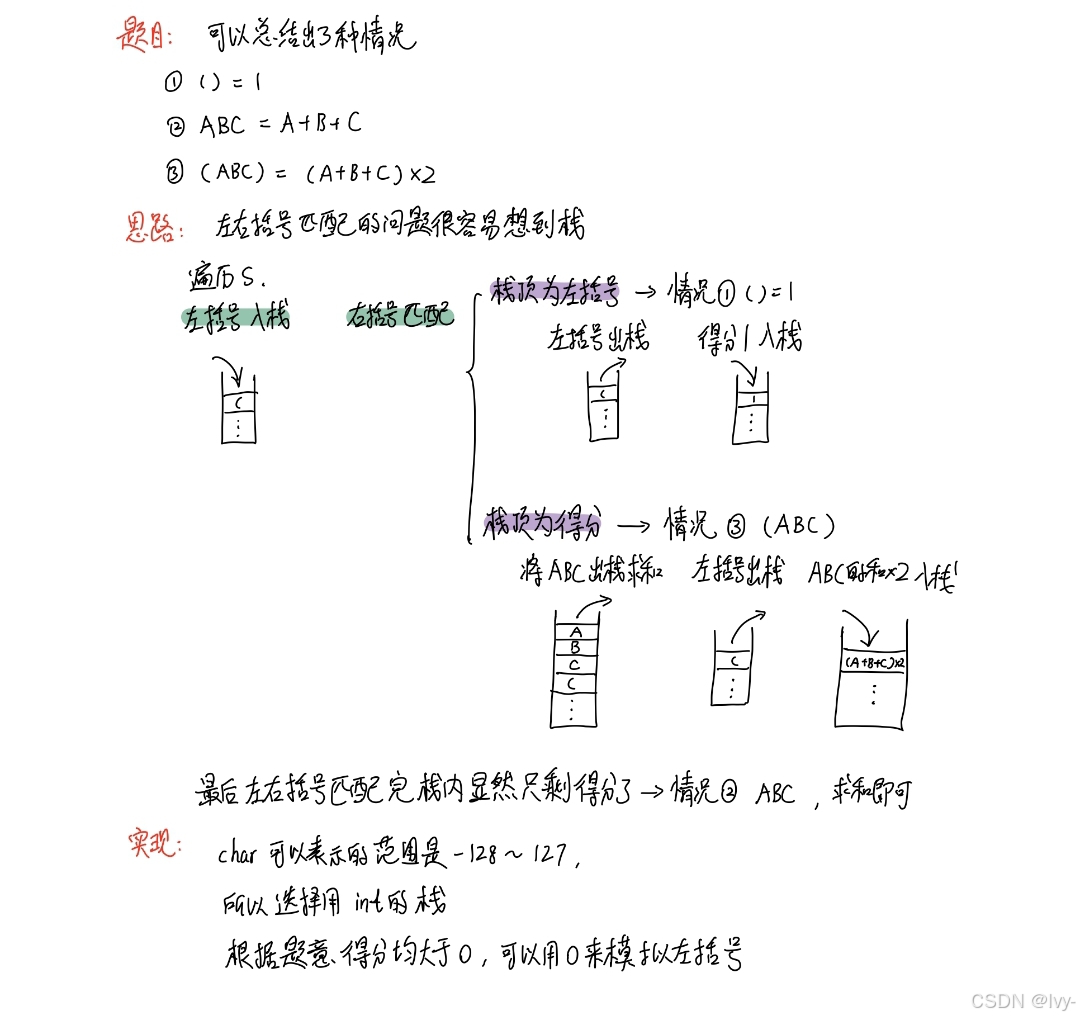
lc856
用栈处理括号字符串,左括号存0,遇右括号时,若栈顶是0(对应“()”)则替换为1
若栈顶是数字(对应“(ABC)”)则累加内部数字再乘2
最后把栈里所有分数相加ABC,得到括号的最终分数
class Solution {
public:
int scoreOfParentheses(string S)
{
stack<int> s;
for(char c:S){
if(c=='('){ //遇到左括号入栈,用0模拟
s.push(0);
}
else{ //遇到右括号进行判断
if(s.top()==0){ //栈顶为0即栈顶为左括号,此时为()的情况,得1分
s.pop();
s.push(1);
}
else{ //栈顶不为左括号即为(ABC)的情况,得分为(A+B+C)*2
int inScore=0;
while(s.top()!=0){
inScore+=s.top();
s.pop();
}
s.pop();
s.push(inScore*2);
}
}
}
int score=0;
while(!s.empty()){ //最后栈内都是分数,没有括号了,求和即可
score+=s.top();
s.pop();
}
return score;
}
};
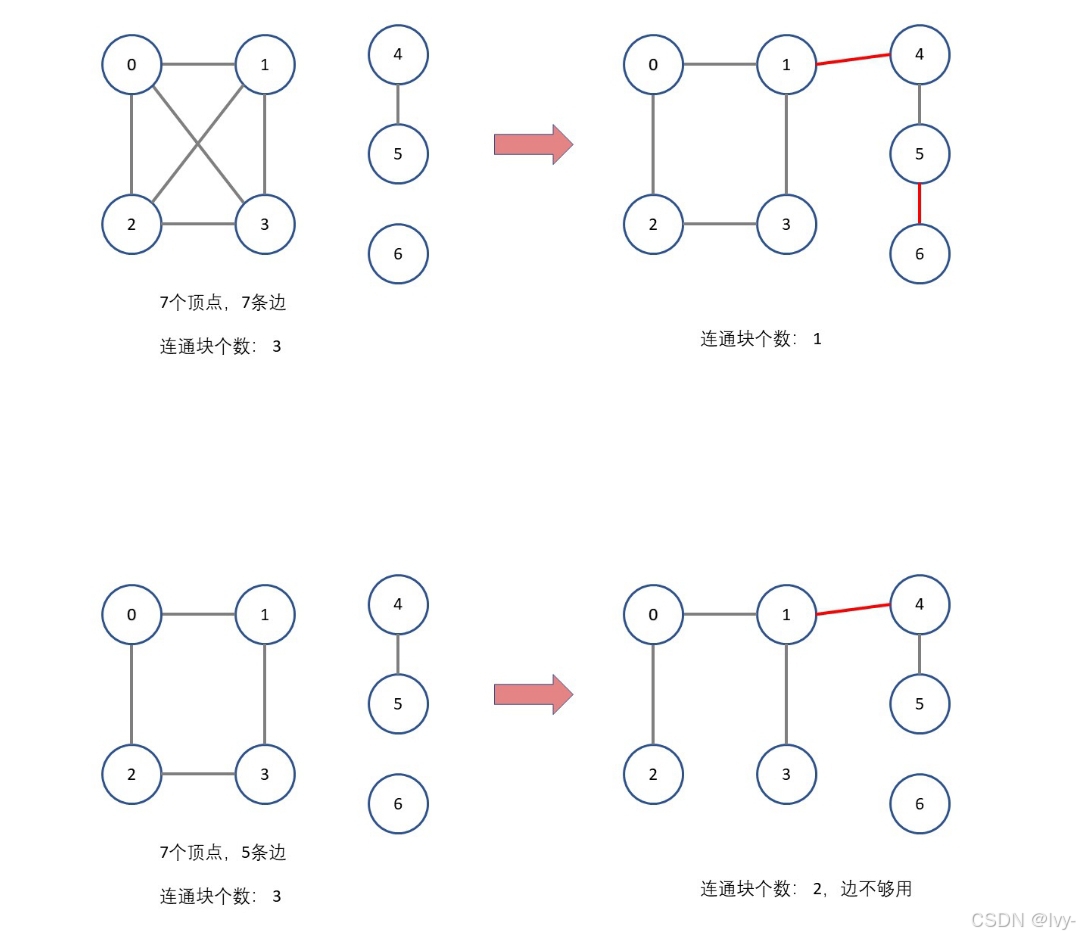
lc1319.
dfs
class Solution {
public:
vector<vector<int>> build_graph(const int& n,const vector<vector<int>>& connections) const{
vector<vector<int>> graph(n,vector<int>());
for(auto& edge: connections){
graph[edge[0]].push_back(edge[1]);
graph[edge[1]].push_back(edge[0]);
}
return graph;
}
void dfs(const vector<vector<int>>& graph,unordered_set<int>& visited,int node){
if(visited.count(node))
return;
visited.insert(node);
for(const auto& neighbor: graph[node])
dfs(graph,visited,neighbor);
}
int makeConnected(int n, vector<vector<int>>& connections) {
if(connections.size() < n-1)
return -1;
// 建图
vector<vector<int>> graph = build_graph(n,connections);
unordered_set<int> visited;
int connected_components = 0;
// 遍历顶点
for(int node = 0;node < n;node++){
// 如果没被访问过
if(!visited.count(node)){
connected_components++;
dfs(graph,visited,node);
}
}
return connected_components-1;
}
};
并查集写法
class UnionFind
{
private:
unordered_map<int,int> father;
int num_of_sets;
public:
UnionFind(int size): num_of_sets(size){
for(int i = 0;i < size;i++)
father[i] = i;
}
int get_num_of_sets(){
return num_of_sets;
}
int find(int x){
if(father[x] == x) return x;
// 路径压缩
father[x] = find(father[x]);
return father[x];
}
bool is_connected(int x,int y){
return find(x) == find(y);
}
void merge(int x,int y){
father[find(x)] = find(y);
num_of_sets--;
}
};
class Solution {
public:
int makeConnected(int n, vector<vector<int>>& connections) {
if(connections.size() < n-1) return -1;
UnionFind uf(n);
for(auto& edge: connections){
if(!uf.is_connected(edge[0],edge[1])){
uf.merge(edge[0],edge[1]);
}
}
return uf.get_num_of_sets() - 1;
}
};








)







—— 数据库安全RedisCouchDBH2database未授权CVE)


