参考：
https://www.bilibili.com/video/BV1MF4m1V7e3/
https://blog.csdn.net/2401_86810419/article/details/148811121
https://www.bilibili.com/video/BV1cz421872F?t=233.9
https://wuli.wiki/online/SphHar.html
https://zhuanlan.zhihu.com/p/467466131
特别指出的是SY__007的3DGS较真系列，对本文有极大的启发和参考价值，下文有很多截图也直接来自视频，强烈推荐大家移步小破站，去观看视频。
做雪球?
What is splatting？
关于Splat，在英语中作抛雪球打击到墙面的拟声词。
Splatting是一种体渲染的方法：将3D物体渲染到2D平面
与NeRF中的渲染方法的差异：
NeRF中使用Ray-casting（类似射线求积分）：是计算像素点收到发光粒子的影响来生成图像。
3DGS中使用Splatting这种主动的方法，计算发光粒子如何影响像素点
Splatting算法的核心：
1.选择雪球
2.抛掷雪球：从3D投影到2D，得到足迹（footprint）
3.加以合成，得到最终的图像
一：为什么使用核（雪球，Gaussian）：
基于Gaussian的数学性质：
1.Gaussian本身是闭合的椭球，经过仿射变换后依旧是封闭的
2.高维Gaussian降维（沿某个轴进行积分）之后依旧是Gaussian
对于椭球Gaussian：
其中x是三维空间中的点，
μ是高斯分布的均值向量，表示Gaussian的中心点位置
Σ是协方差矩阵，描述Gaussian在3D空间中的形状和方向，它是半正定的
为什么这是一个椭球？
首先去了解 协方差矩阵。
对于Gauss分布：
一维：形状由 均值&方差 决定
高维：形状由 均值&协方差矩阵 决定
对于协方差矩阵：
-
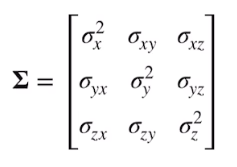
是一个对称矩阵，决定高斯分布形状
-
对角线上元素为x轴/y轴/z轴的方差
-
反斜对角线上的值为协方差，表示x和y，x和z........的线性相关程度
这里直接用SY__007写的：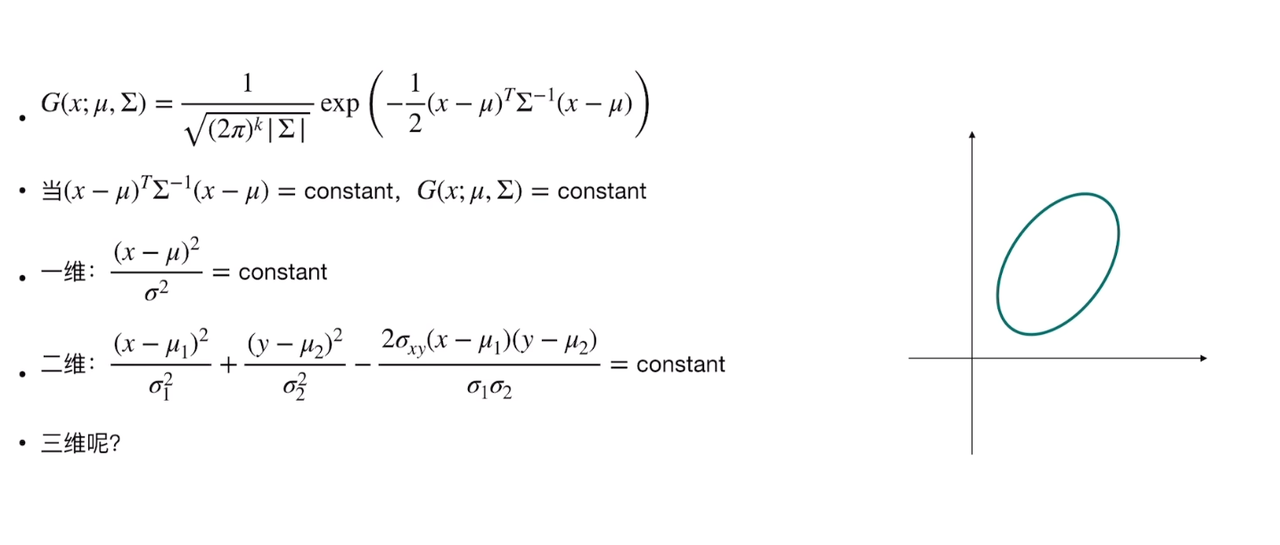
抛雪球
如何进行参数变换？
从3D->像素的过程：
观测变换
观测变换：从世界坐标系-->相机坐标系
投影变换
投影变换：正交投影 、透视投影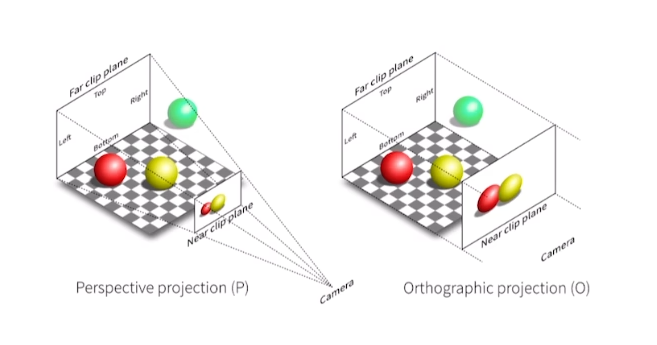
正交投影：
对于立方体[l,r]*[b,t]*[f,n]
1.平移到原点
2.立方体缩放至[-1,1]^3的正方体空间内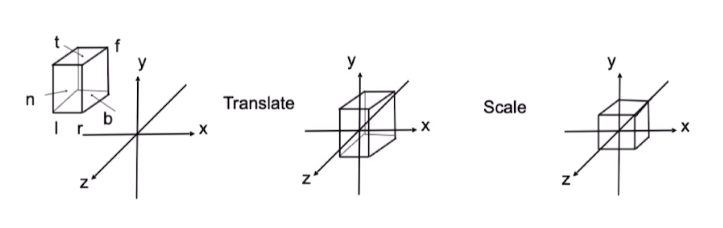
总的来说就是进行了仿射变换，
如题所给的例子的仿射变换即是：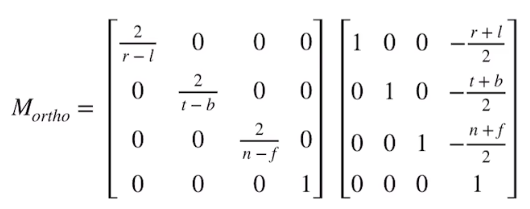
A这里是缩放矩阵
B为平移矩阵
在正交投影中，我们没有考虑对于原本的长方体的长和宽的比例不同，导致的缩放比例不同，其实产生了畸变，这个问题会在之后的视口变换解决
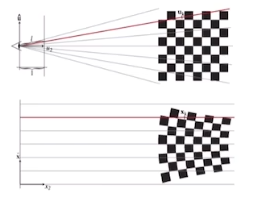
透视投影：
透视投影需要满足近大远小的条件
对于视锥，我们先把他变换为‘立方体’，再进行正交投影
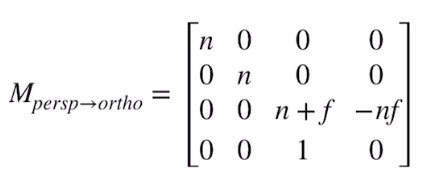
数学过程实在懒得写了，这里直接放上作者手稿一张
问题？：
透视投影是非线性的，也就是非放射变换，但是高斯椭球经过仿射变换后是高斯，但非仿射变换就不一定。
视口变换：
我们从简化的图形渲染管线开始：
3D 顶点 → 模型变换 → 视图变换 → 投影变换 → 裁剪 → 标准化设备坐标 → 视口变换 → 屏幕像素
之前的变换已经将顶点从”模型局部坐标“转换成NDC空间坐标，以OpenGL为例，正交投影下为[-1,1]×[-1,1]×[-1,1]
视口变换的目的就是把可见区域的标准化坐标，映射到显示器的实际像素区域，让图形真正显示在屏幕上。
视口变换的数学实现
核心是缩放+平移的组合，把NDC范围映射到屏幕视口的像素范围：
(1)以OpenGL经典的[-1.1]立方体为例（xy对应屏幕二维，z用于深度缓冲）：
-
NDC的x范围:
-
NDC的y范围：
-
NDC的z范围：
(或者[0,1],这取决于深度缓冲装置)
(2)目标视口的像素范围
假设屏幕视口的：
-
左下角像素坐标：（x0,y0）（比如窗口内视口偏移，或全屏时 (0,0)）
-
宽度：width（像素数，如 800 ）、高度：height（像素数，如 600 ）
-
深度范围（可选，用于深度缓冲）：[zNear,zFar]（比如 [0,255] 或浮点深度 ）
(3)视口变换矩阵与公式
视口变换通过缩放矩阵+平移矩阵,实现对标准化坐标,变换后得到屏幕像素坐标
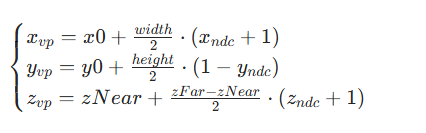
用矩阵形式（齐次坐标下）可以表示为：
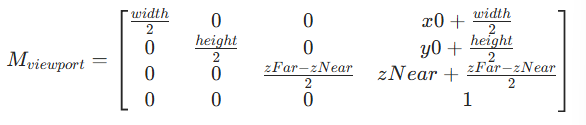
对于进行拆解
1.缩放部分：
-
x方向：
把[-1,1]缩放为[0,width]范围；
-
y方向：
把[-1,1]缩放为[0,height]范围，但考虑到屏幕坐标系一般y轴"向下为上”（与NDC相反），所以使用
反转；
-
z方向：
把[-1,1]缩放为[zNear,zFar]（深度缓冲的实际范围）
2.平移部分
-
x 平移
，让缩放后的 [0,width] 起点对齐视口左下角 x0；
-
y 平移
，同理对齐视口左下角 y0；
-
z 平移
，让缩放后的深度对齐 zNear 起点。
视口变换的实际作用：
-
从虚拟坐标到物理屏幕
-
支持多视角渲染
-
深度缓冲的落地
光栅化：
1.光栅化的位置：渲染管线‘矢量-->像素’转换
简单渲染管线流程为：
3D 顶点 → 变换（模型/视图/投影）→ 裁剪 → 标准化设备坐标（NDC）→ 光栅化 → 像素着色 → 帧缓冲 → 屏幕
-
前面的变换，把顶点转成抽象的数学坐标（如NDC空间下的[-1,1]立方体）
-
光栅化要解决：如何把这些矢量图元拆解成屏幕上的离散像素，让每个像素知道“属于哪个图元，该染什么颜色”
2.光栅化的核心任务:图元的“离散化”
（1）输入：图元的“数学描述”
以三角形为例（图形学的最基础图元，复杂模型由三角形拼接），输入是三个顶点的坐标（NDC或视口变换后的屏幕坐标），以及顶点附带的属性（颜色、法向量、纹理坐标等）。
（2）输出：像素的“归属与属性”
输出是覆盖这些三角形的所有像素，并为每个像素插值计算属性（比如/顶点颜色查指出像素颜色，纹理坐标插值出采样位置），供后续像素着色器处理。
3.光栅化的关键步骤
（1）三角形 setup（配置）
计算三角形的边方程和包围盒
-
先找出三角形在屏幕上的最小包围矩形（AABB）,只遍历这个范围内的像素，减少计算量；
-
推导三角形三条边的数学方程（如ax+by+c=0）,用于判断i像素是否在三角形内
（2）三角形traversal(遍历)
-
对包围盒捏的每个像素（或'采样点'），用便方程判断是否在三角形内（比如OpenGL的“winding order”规则，或计算重心坐标）。
-
若像素在三角形内，就标记为属于该三角形，并进入属性插值阶段
（3）属性插值
三角形三个顶点有属性（如颜色、纹理坐标
