目录

1. 验证栈序列

1.1 题目解析

1.2 解法

1.3 代码实现

2. N叉树的层序遍历

2.1 题目解析

2.2 解法

2.3 代码实现

---

1. 验证栈序列

https://leetcode.cn/problems/validate-stack-sequences/description/

给定 pushed 和 popped 两个序列，每个序列中的 值都不重复，只有当它们可能是在最初空栈上进行的推入 push 和弹出 pop 操作序列的结果时，返回 true；否则，返回 false 。

示例 1：

输入：pushed = [1,2,3,4,5], popped = [4,5,3,2,1]
输出：true
解释：我们可以按以下顺序执行：
push(1), push(2), push(3), push(4), pop() -> 4,
push(5), pop() -> 5, pop() -> 3, pop() -> 2, pop() -> 1

示例 2：

输入：pushed = [1,2,3,4,5], popped = [4,3,5,1,2]
输出：false
解释：1 不能在 2 之前弹出。

提示：

• 1 <= pushed.length <= 1000
• 0 <= pushed[i] <= 1000
• pushed 的所有元素 互不相同
• popped.length == pushed.length
• popped 是 pushed 的一个排列

1.1 题目解析

题目本质：
判断一对 pushed / popped 序列能否由同一“从空开始”的栈操作产生。抽象成：按 pushed 顺序“尽量入栈”，每当栈顶等于 popped 的下一个元素就立刻出栈，最终是否能把 popped 全部匹配并清空栈。

常规解法：
最直观就是模拟栈：顺序把 pushed[i] 入栈；每次入栈后，若栈顶恰好等于 popped[j]，就持续出栈并前进 j。

问题分析：
该题无需复杂数据结构，也不需要回溯。因为所有元素互不相同，且 popped 是 pushed 的一个排列，所以“能弹就弹”的贪心策略不会错；若某个 popped[j] 迟迟在栈顶见不到，那就永远见不到（后续只会把更多不同元素压在它上面）。

思路转折：
要想高效 → 直接一次线性扫描 + 栈模拟即可：

• 扫过 pushed 时入栈；

• 每次入栈后，尽可能匹配 popped 进行弹栈；

• 扫描结束后栈应为空（或 j == n）。
  时间 O(n)，空间 O(n)，是本题最优做法。

1.2 解法

算法思想：
维护指针 i 遍历 pushed、指针 j 指向 popped 的下一个待弹元素；循环中把 pushed[i] 入栈，然后在 stack.peek() == popped[j] 时不断 pop() 与 j++；最终栈空则返回 true。

i）初始化空栈，i = 0, j = 0。

ii）外层循环：当 i < pushed.length：

• push(pushed[i])，i++；

• 内层循环：当 stack.peek() == popped[j]：

  • pop()，j++。

iii）全部处理后，返回 stack.isEmpty()（或判断 j == popped.length）。

易错点：

• 等于就弹，且要连续弹：入栈后别忘了用 while 连续匹配 popped[j]，直到不等为止。

• 边界与空栈判断：写 peek() 前要保证栈非空（示例代码里通过条件顺序或 isEmpty() 规避）。

• 指针前进时机：i 只在入栈后前进；j 只在成功弹出后前进。

1.3 代码实现

class Solution {public boolean validateStackSequences(int[] pushed, int[] popped) {// 可用 Deque<Integer> stack = new ArrayDeque<>(); 更高效java.util.Stack<Integer> stack = new java.util.Stack<>();int i = 0, j = 0, n = pushed.length;while (i < n) {stack.push(pushed[i++]);                 // 先按 pushed 顺序入栈// 只要栈顶等于 popped[j]，就连续弹出并推进 jwhile (!stack.isEmpty() && stack.peek() == popped[j]) {stack.pop();j++;}}// 若能完全匹配，栈应被清空（等价于 j == n）return stack.isEmpty();}
}

复杂度分析：

• 时间复杂度：O(n)。每个元素最多入栈一次、出栈一次。

• 空间复杂度：O(n)。最坏情况下栈会临时存放尚未匹配的元素。

2. N叉树的层序遍历

https://leetcode.cn/problems/n-ary-tree-level-order-traversal/description/

给定一个 N 叉树，返回其节点值的层序遍历。（即从左到右，逐层遍历）。

树的序列化输入是用层序遍历，每组子节点都由 null 值分隔（参见示例）。

示例 1：

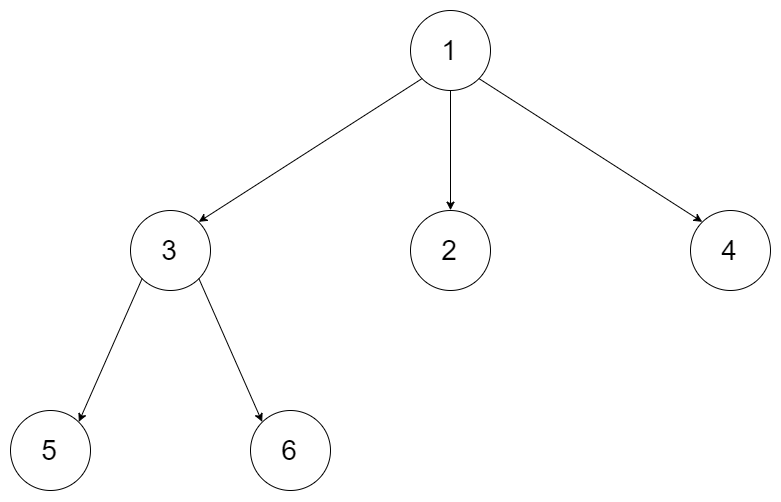
输入：root = [1,null,3,2,4,null,5,6]
输出：[[1],[3,2,4],[5,6]]

示例 2：

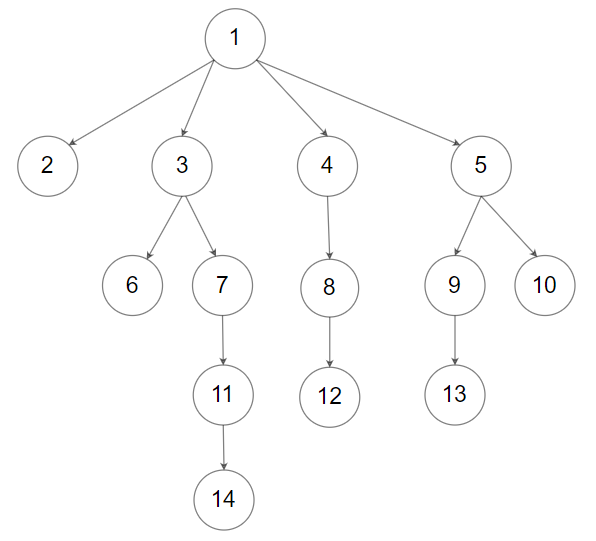
输入：root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
输出：[[1],[2,3,4,5],[6,7,8,9,10],[11,12,13],[14]]

提示：

• 树的高度不会超过 1000
• 树的节点总数在 [0, 104] 之间

2.1 题目解析

题目本质：
在一棵 N 叉树上做层序遍历（Level Order Traversal）：从根开始，逐层、从左到右收集结点值，形成二维列表。

常规解法：
用队列做 BFS。根结点先入队；每一轮“锁定当前层的队列大小 sz”，弹出 sz 个结点，把它们的值放到当前层列表，并把它们的子结点（若非空）全部入队；层结束后把该层列表放进答案。。

问题分析：

• 本题没有回溯或复杂剪枝，关键只是正确分层与子结点判空。

• 题目上限：节点数 ≤ 1e4、树高 ≤ 1000。BFS 时间 O(n)、空间 O(w)（w 为最大宽度）都可接受。

• DFS 也能做层序（记录 depth），但极深树形递归层数会接近 1000，BFS 更稳妥。

思路转折：
要想写得又对又稳 → 一次线性 BFS + 锁层大小：

• 入队根；

• 循环直到队空：先记 sz = q.size()，弹 sz 次组成一层；

• 遍历子结点时判空，避免 NullPointerException 与把 null 入队。

2.2 解法

算法思想：
维护队列 q。
1）若 root == null 直接返回空结果；
2）root 入队；
3）当队列非空，令 sz = q.size()：循环 sz 次，弹出结点 node，把 node.val 记入本层；若 node.children != null，则将非空子结点依次入队；
4）把本层列表加入答案。重复直至队空。

步骤：

i）处理空树：返回 []。

ii）初始化：Queue<Node> q = new ArrayDeque<>(); q.offer(root);

iii）外层循环：while (!q.isEmpty())：

• int sz = q.size(); List<Integer> level = new ArrayList<>(sz);

• 重复 sz 次：

  • Node node = q.poll(); level.add(node.val);

  • 若 node.children != null：遍历每个子结点 ch，if (ch != null) q.offer(ch);

• result.add(level);

iiii）返回 result。

易错点：

• children 判空：node.children 可能为 null，遍历前要判空。

• 不要入队 null：遍历子结点时 if (ch != null) 再 offer。

• 锁层大小：务必先取 sz = q.size()，再弹 sz 次，防止跨层污染。

• API 使用：队列用 offer/poll/peek，不要用 pop（那是栈/双端队列当栈用的）。

• 实现类选择：Queue 不能 new Queue<>()；用 ArrayDeque<>（相对 LinkedList 更高效、足够）。

• 空树返回值：不要返回 null，而是空列表。

• 泛型简写：new ArrayList<>()、new ArrayDeque<>() 更简洁。

2.3 代码实现

/*
// Definition for a Node.
class Node {public int val;public List<Node> children;public Node() {}public Node(int _val) { val = _val; }public Node(int _val, List<Node> _children) {val = _val; children = _children;}
};
*/import java.util.*;class Solution {public List<List<Integer>> levelOrder(Node root) {List<List<Integer>> result = new ArrayList<>();if (root == null) return result;  // 空树Queue<Node> q = new ArrayDeque<>();q.offer(root);while (!q.isEmpty()) {int sz = q.size();                   // 锁定本层大小List<Integer> level = new ArrayList<>(sz);for (int i = 0; i < sz; i++) {Node node = q.poll();            // 出队当前层结点level.add(node.val);if (node.children != null) {     // 判空再遍历子结点for (Node ch : node.children) {if (ch != null) q.offer(ch);}}}result.add(level);                   // 收录本层}return result;}
}

复杂度分析：

• 时间复杂度：O(n)，每个结点至多入队/出队一次。

• 空间复杂度：O(w)，其中 w 为树在某一层的最大结点数（最坏 O(n)）。