A.深搜与广搜(重点掌握!!!!)
深搜类似于回溯法
- 搜索方向,是认准一个方向搜,直到碰壁之后再换方向
- 换方向是撤销原路径,改为节点链接的下一个路径,回溯的过程。
广搜能保存我们要遍历过的元素的容器就可以,队列、栈、数组都是OK。
- 用队列的话,就是保证每一圈都是一个方向去转,例如统一顺时针或者逆时针。因为队列是先进先出,加入元素和弹出元素的顺序是没有改变的。
- 如果用栈的话,就是第一圈顺时针遍历,第二圈逆时针遍历,第三圈有顺时针遍历。因为栈是先进后出,加入元素和弹出元素的顺序改变了
1.可达路径
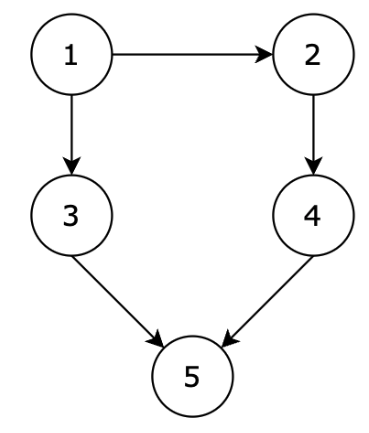
感悟:找出从1到5的所有路径,深度优先搜索的代码其实和回溯法很像,节点入path,递归+回溯
var result [][]int
var path []int
func dfs(graph [][]int, x, n int) {// 当前遍历的节点x 到达节点nif x == n { // 找到符合条件的一条路径temp := make([]int, len(path))copy(temp, path)result = append(result, temp)return}for i := 1; i <= n; i++ { // 遍历节点x链接的所有节点if graph[x][i] == 1 { // 找到 x链接的节点path = append(path, i) // 遍历到的节点加入到路径中来dfs(graph, i, n) // 进入下一层递归path = path[:len(path)-1] // 回溯,撤销本节点}}
}
2.岛屿数量
方法一:深搜---模板题,后期要总结!!!!
package main
import "fmt"var dir = [][]int{{0, 1}, // 右{1, 0}, // 下{-1, 0}, // 上{0, -1}, // 左
}
func dfs(graph [][]int, visited [][]bool,x,y int){for i := range dir{nextx := x + dir[i][0]nexty := y + dir[i][1]if nextx < 0||nextx >= len(graph)||nexty < 0||nexty >=len(graph[0]){continue}if !visited[nextx][nexty] && graph[nextx][nexty] == 1{visited[nextx][nexty] = truedfs(graph,visited,nextx,nexty)}}
}
func main(){var n,m intfmt.Scan(&n,&m)graph := make([][]int,n)for i := range graph{graph[i] = make([]int,m)}for i := 0;i < n; i++{for j := 0;j < m; j++{fmt.Scan(&graph[i][j])}}visited := make([][]bool,n)for i := range visited{visited[i] = make([]bool,m)}var res intfor i := 0;i < n;i++{for j := 0;j < m;j++{if !visited[i][j] && graph[i][j] == 1{visited[i][j] = trueres++dfs(graph,visited,i,j)//将和他相连的陆地都标记上true}}}fmt.Println(res)
}方法二:广搜---模板题---后期要总结!!!
package main
import ("fmt""container/list"
)var dir = [4][2]int{{0, 1}, // 右{1, 0}, // 下{-1, 0}, // 上{0, -1}, // 左
}
func bfs(graph [][]int, visited [][]bool,x,y int){queue := list.New()queue.PushBack([2]int{x,y})visited[x][y] = truefor queue.Len() > 0{cur := queue.Remove(queue.Front()).([2]int)curx,cury := cur[0],cur[1]for i := range dir{nextx := curx + dir[i][0]nexty := cury + dir[i][1]if nextx < 0 || nexty < 0||nextx >= len(graph)||nexty >= len(graph[0]){continue}if !visited[nextx][nexty] && graph[nextx][nexty] == 1{visited[nextx][nexty] = truequeue.PushBack([2]int{nextx,nexty})}}}
}func main(){var n,m intfmt.Scan(&n,&m)graph := make([][]int,n)for i := range graph{graph[i] = make([]int,m)}for i := 0;i < n;i++{for j := 0;j < m;j++{fmt.Scan(&graph[i][j])}}visited := make([][]bool,n)for i := range visited{visited[i] = make([]bool,m)}var res intfor i := 0;i < n;i++{for j := 0;j < m;j++{if !visited[i][j] && graph[i][j] == 1{visited[i][j] = trueres++bfs(graph,visited,i,j)//将和他相连的陆地都标记上true}}}fmt.Println(res)
}3.岛屿最大面积
感悟:本题就在模板题的基础之上统计面积!!!
package main
import "fmt"var dir = [][]int{{0, 1}, // 右{1, 0}, // 下{-1, 0}, // 上{0, -1}, // 左
}
var count int
func dfs(graph [][]int, visited [][]bool,x,y int){for i := range dir{nextx := x + dir[i][0]nexty := y + dir[i][1]if nextx < 0||nextx >= len(graph)||nexty < 0||nexty >=len(graph[0]){continue}if !visited[nextx][nexty] && graph[nextx][nexty] == 1{visited[nextx][nexty] = truecount++dfs(graph,visited,nextx,nexty)}}
}
func max(i,j int)int{if i > j{return i}else{return j}
}
func main(){var n,m intfmt.Scan(&n,&m)graph := make([][]int,n)for i := range graph{graph[i] = make([]int,m)}for i := 0;i < n; i++{for j := 0;j < m; j++{fmt.Scan(&graph[i][j])}}visited := make([][]bool,n)for i := range visited{visited[i] = make([]bool,m)}var res intfor i := 0;i < n;i++{for j := 0;j < m;j++{if !visited[i][j] && graph[i][j] == 1{visited[i][j] = truecount = 1dfs(graph,visited,i,j)res = max(res,count)//将和他相连的陆地都标记上true}}}fmt.Println(res)
}4.孤岛总面积
本题要求找到不靠边的陆地面积,那么我们只要从周边找到陆地然后 通过 dfs或者bfs 将周边靠陆地且相邻的陆地都变成海洋,然后再去重新遍历地图 统计此时还剩下的陆地就可以了。
package mainimport ("container/list""fmt"
)// 四个方向的偏移量
var dir = [][]int{{0, 1}, // 右{1, 0}, // 下{-1, 0}, // 上{0, -1}, // 左
}// BFS函数,用于标记并清除连通的陆地
func bfs(grid [][]int, x, y int) {// 使用list作为队列que := list.New()que.PushBack([2]int{x, y})grid[x][y] = 0 // 加入队列后立即标记为已访问// 队列不为空时继续处理for que.Len() > 0 {// 取出队首元素cur := que.Front().Value.([2]int)que.Remove(que.Front())curx, cury := cur[0], cur[1]// 遍历四个方向for i := 0; i < 4; i++ {nextx := curx + dir[i][0]nexty := cury + dir[i][1]// 边界检查if nextx < 0 || nextx >= len(grid) || nexty < 0 || nexty >= len(grid[0]) {continue}// 如果是未访问的陆地,加入队列并标记if grid[nextx][nexty] == 1 {que.PushBack([2]int{nextx, nexty})grid[nextx][nexty] = 0 // 加入队列后立即标记}}}
}func main() {var n, m intfmt.Scan(&n, &m)// 初始化网格grid := make([][]int, n)for i := range grid {grid[i] = make([]int, m)}// 读取网格数据for i := 0; i < n; i++ {for j := 0; j < m; j++ {fmt.Scan(&grid[i][j])}}// 处理左右边界的陆地for i := 0; i < n; i++ {if grid[i][0] == 1 {bfs(grid, i, 0)}if grid[i][m-1] == 1 {bfs(grid, i, m-1)}}// 处理上下边界的陆地for j := 0; j < m; j++ {if grid[0][j] == 1 {bfs(grid, 0, j)}if grid[n-1][j] == 1 {bfs(grid, n-1, j)}}// 统计剩余的陆地(孤岛)数量count := 0for i := 0; i < n; i++ {for j := 0; j < m; j++ {if grid[i][j] == 1 {count++}}}fmt.Println(count)
}5.沉没孤岛
感悟:这道题只不过遇到陆地就加一,最后都减1。和上道题一个思路
package mainimport ("container/list""fmt"
)// 四个方向的偏移量
var dir = [][]int{{0, 1}, // 右{1, 0}, // 下{-1, 0}, // 上{0, -1}, // 左
}// BFS函数,用于标记并清除连通的陆地
func bfs(grid [][]int, x, y int) {// 使用list作为队列que := list.New()que.PushBack([2]int{x, y})grid[x][y] = 2 // 加入队列后立即标记为已访问// 队列不为空时继续处理for que.Len() > 0 {// 取出队首元素cur := que.Front().Value.([2]int)que.Remove(que.Front())curx, cury := cur[0], cur[1]// 遍历四个方向for i := 0; i < 4; i++ {nextx := curx + dir[i][0]nexty := cury + dir[i][1]// 边界检查if nextx < 0 || nextx >= len(grid) || nexty < 0 || nexty >= len(grid[0]) {continue}// 如果是未访问的陆地,加入队列并标记if grid[nextx][nexty] == 1 {que.PushBack([2]int{nextx, nexty})grid[nextx][nexty] = 2 // 加入队列后立即标记}}}
}func main() {var n, m intfmt.Scan(&n, &m)// 初始化网格grid := make([][]int, n)for i := range grid {grid[i] = make([]int, m)}// 读取网格数据for i := 0; i < n; i++ {for j := 0; j < m; j++ {fmt.Scan(&grid[i][j])}}// 处理左右边界的陆地for i := 0; i < n; i++ {if grid[i][0] == 1 {bfs(grid, i, 0)}if grid[i][m-1] == 1 {bfs(grid, i, m-1)}}// 处理上下边界的陆地for j := 0; j < m; j++ {if grid[0][j] == 1 {bfs(grid, 0, j)}if grid[n-1][j] == 1 {bfs(grid, n-1, j)}}// 统计剩余的陆地(孤岛)数量for i := 0; i < n; i++ {for j := 0; j < m; j++ {if grid[i][j] != 0 {grid[i][j]--}}}for i := 0;i < n;i++{for j := 0;j < m-1;j++{fmt.Printf("%d ",grid[i][j])}fmt.Println(grid[i][m-1])}
}6.水流问题
从第一组边界逆流而上,第二组边界也逆流而上,然后同时标记过的点就是答案
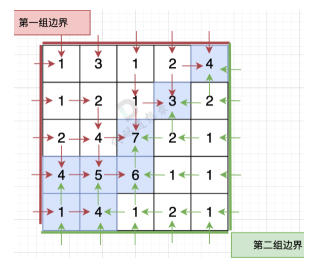
package mainimport "fmt"var n, m int
var dir = [][]int{{-1, 0}, // 上{0, -1}, // 左{1, 0}, // 下{0, 1}, // 右
}// dfs 函数:从(x,y)开始遍历,只向不低于当前高度的方向移动
func dfs(grid [][]int, visited [][]bool, x, y int) {if visited[x][y] {return}visited[x][y] = truefor i := 0; i < 4; i++ {nextx := x + dir[i][0]nexty := y + dir[i][1]// 边界检查if nextx < 0 || nextx >= n || nexty < 0 || nexty >= m {continue}// 只向不低于当前高度的方向遍历(从低向高)if grid[x][y] > grid[nextx][nexty] {continue}dfs(grid, visited, nextx, nexty)}
}func main() {fmt.Scan(&n, &m)// 初始化网格grid := make([][]int, n)for i := range grid {grid[i] = make([]int, m)}// 读取网格数据for i := 0; i < n; i++ {for j := 0; j < m; j++ {fmt.Scan(&grid[i][j])}}// 初始化两个边界访问标记数组firstBorder := make([][]bool, n)secondBorder := make([][]bool, n)for i := range firstBorder {firstBorder[i] = make([]bool, m)secondBorder[i] = make([]bool, m)}// 从最左列和最右列开始遍历for i := 0; i < n; i++ {dfs(grid, firstBorder, i, 0) // 第一组边界:最左列dfs(grid, secondBorder, i, m-1) // 第二组边界:最右列}// 从最上行和最下行开始遍历for j := 0; j < m; j++ {dfs(grid, firstBorder, 0, j) // 第一组边界:最上行dfs(grid, secondBorder, n-1, j) // 第二组边界:最下行}// 输出同时被两组边界遍历到的节点坐标for i := 0; i < n; i++ {for j := 0; j < m; j++ {if firstBorder[i][j] && secondBorder[i][j] {fmt.Printf("%d %d\n", i, j)}}}
}
7.建造最大孤岛
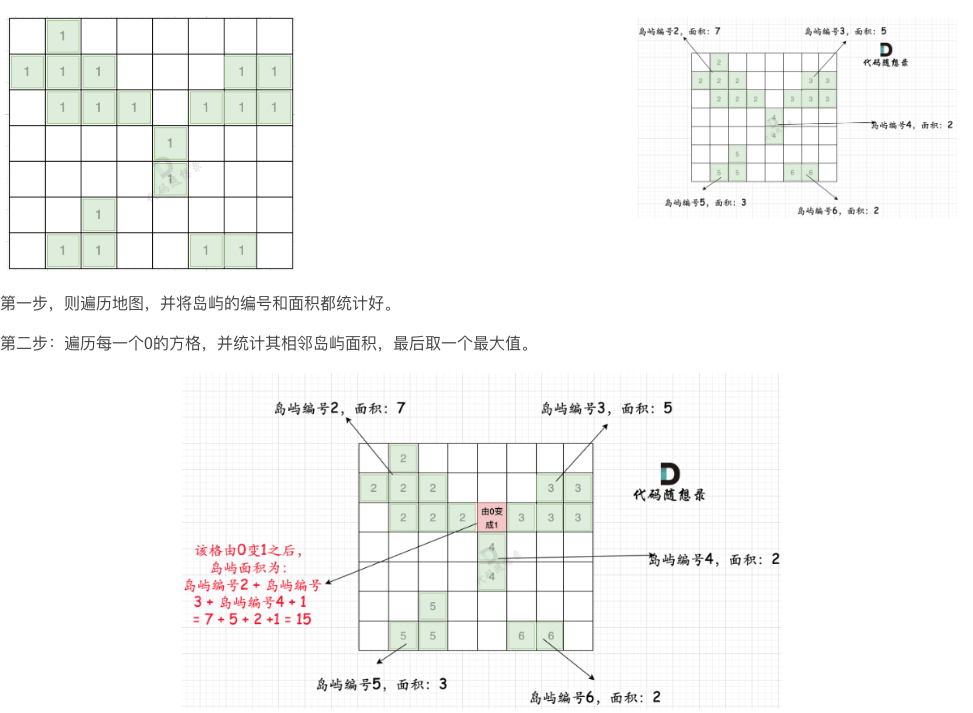
package mainimport "fmt"var n, m int
var dir = [][]int{{-1, 0}, // 上{0, -1}, // 左{1, 0}, // 下{0, 1}, // 右
}// dfs 函数:从(x,y)开始遍历,只向不低于当前高度的方向移动
func dfs(grid [][]int, visited [][]bool, x, y int) {if visited[x][y] {return}visited[x][y] = truefor i := 0; i < 4; i++ {nextx := x + dir[i][0]nexty := y + dir[i][1]// 边界检查if nextx < 0 || nextx >= n || nexty < 0 || nexty >= m {continue}// 只向不低于当前高度的方向遍历(从低向高)if grid[x][y] > grid[nextx][nexty] {continue}dfs(grid, visited, nextx, nexty)}
}func main() {fmt.Scan(&n, &m)// 初始化网格grid := make([][]int, n)for i := range grid {grid[i] = make([]int, m)}// 读取网格数据for i := 0; i < n; i++ {for j := 0; j < m; j++ {fmt.Scan(&grid[i][j])}}// 初始化两个边界访问标记数组firstBorder := make([][]bool, n)secondBorder := make([][]bool, n)for i := range firstBorder {firstBorder[i] = make([]bool, m)secondBorder[i] = make([]bool, m)}// 从最左列和最右列开始遍历for i := 0; i < n; i++ {dfs(grid, firstBorder, i, 0) // 第一组边界:最左列dfs(grid, secondBorder, i, m-1) // 第二组边界:最右列}// 从最上行和最下行开始遍历for j := 0; j < m; j++ {dfs(grid, firstBorder, 0, j) // 第一组边界:最上行dfs(grid, secondBorder, n-1, j) // 第二组边界:最下行}// 输出同时被两组边界遍历到的节点坐标for i := 0; i < n; i++ {for j := 0; j < m; j++ {if firstBorder[i][j] && secondBorder[i][j] {fmt.Printf("%d %d\n", i, j)}}}
}
8.岛屿周长
package mainimport ("bufio""fmt""os""strconv""strings"
)func main() {scanner := bufio.NewScanner(os.Stdin)scanner.Scan()line := scanner.Text()n, m := parseInput(line)// 初始化 gridgrid := make([][]int, n)for i := range grid {grid[i] = make([]int, m)}// 读入 grid 数据for i := 0; i < n; i++ {scanner.Scan()line := scanner.Text()values := parseLine(line, m)for j := 0; j < m; j++ {grid[i][j] = values[j]}}sum := 0 // 陆地数量cover := 0 // 相邻数量for i := 0; i < n; i++ {for j := 0; j < m; j++ {if grid[i][j] == 1 {sum++ // 统计总的陆地数量// 统计上边相邻陆地if i-1 >= 0 && grid[i-1][j] == 1 {cover++}// 统计左边相邻陆地if j-1 >= 0 && grid[i][j-1] == 1 {cover++}// 为什么没统计下边和右边? 因为避免重复计算}}}fmt.Println(sum*4 - cover*2)
}// parseInput 解析 n 和 m
func parseInput(line string) (int, int) {parts := strings.Split(line, " ")n, _ := strconv.Atoi(parts[0])m, _ := strconv.Atoi(parts[1])return n, m
}// parseLine 解析一行中的多个值
func parseLine(line string, count int) []int {parts := strings.Split(line, " ")values := make([]int, count)for i := 0; i < count; i++ {values[i], _ = strconv.Atoi(parts[i])}return values
}
9.字符串接龙
1、图中的线是如何连在一起的
在搜索的过程中,我们可以枚举,用26个字母替换当前字符串的每一个字符,在看替换后 是否在 strList里出现过,就可以判断两个字符串是否是链接的。
2、起点和终点的最短路径长度
首先题目中并没有给出点与点之间的连线,而是要我们自己去连,条件是字符只能差一个。所以判断点与点之间的关系,需要判断是不是差一个字符,如果差一个字符,那就是有链接。然后就是求起点和终点的最短路径长度,在无权图中,求最短路,用深搜或者广搜就行,没必要用最短路算法。在无权图中,用广搜求最短路最为合适,广搜只要搜到了终点,那么一定是最短的路径。因为广搜就是以起点中心向四周扩散的搜索。
另外需要有一个注意点:
- 本题是一个无向图,需要用标记位,标记着节点是否走过,否则就会死循环!
- 使用哈希表来检查字符串是否出现在字符串集合里更快一些
这道题好难啊!!!(需要二刷)
package main
import("fmt"
)
var count int
func bfs(start,end string,strset map[string]bool)int{visited := make(map[string]int)que := []string{start}visited[start] = 1for len(que) > 0{word := que[0]que = que[1:]path := visited[word]for i := 0;i < len(word);i++{newWord := []byte(word)for j := 0;j < 26;j++{newWord[i] = byte('a'+j)newString := string(newWord)if newString == end{return path + 1}if strset[newString] && visited[newString]==0{//当前单词没有遍历过且新单词在给定的集合当中visited[newString] = path + 1que = append(que,newString)}}}}return 0//没找到
}func main(){var num intfmt.Scan(&num)var start,end,str stringfmt.Scan(&start,&end)strset := make(map[string]bool,num)for i := 0;i < num;i++{fmt.Scan(&str)strset[str] = true}result := bfs(start,end,strset)fmt.Println(result)
}10.有向图的完全可达性
如果是无权的。邻接矩阵就是:如果a和b相连接,a和c连接,那么graph[a][b] = 1.graph[a][c] = 1。如果是邻接表,那么graph[a] = [b,c]
思路:构建邻接表,如果遇到了没有经历过的节点visited置为true。随后遍历他的邻接表。如果遇到新的节点,就接着递归遍历,并且置为true。直到最后。
package mainimport ("fmt"
)func dfs(graph [][]int, key int, visited []bool) {visited[key] = truefor _,neighbor := range graph[key]{if visited[neighbor] == false{dfs(graph,neighbor,visited)}}
}func main(){var n, k intfmt.Scan(&n, &k)//n个节点,k个边graph := make([][]int,n+1)for i := 0;i < k;i++{var u,v intfmt.Scan(&u,&v)graph[u] = append(graph[u],v) }visited := make([]bool,n+1)dfs(graph,1,visited)for i := 1; i <= n; i++ {if !visited[i] {fmt.Println(-1)return}}fmt.Println(1)
}
11.单词接龙
感悟:这道题的本质和字符串接龙是一模一样的。。下午刷完,晚上看这道题就晕了。类似于层序遍历。
func ladderLength(beginWord string, endWord string, wordList []string) int {wordSet := make(map[string]bool,len(wordList))for _,word := range wordList{wordSet[word] = true}if !wordSet[endWord]{return 0}visited := make(map[string]int)visited[beginWord] = 1que := []string{beginWord}for len(que) > 0{cur := que[0]que = que[1:]//出队列path := visited[cur]for i := 0;i < len(cur);i++{newstr := []byte(cur)for j := 0;j < 26;j++{newstr[i] = byte('a'+j)nextword := string(newstr)if nextword == endWord{return path + 1//找到了}if visited[nextword] == 0 && wordSet[nextword]{//能找到,但是没有遍历过visited[nextword] = path + 1que = append(que,nextword)}}}} return 0
}12.钥匙和房间
感悟:这道题的本质就是图的连通性的问题。每个房间对应个节点,房间里的钥匙对应节点间的“边”。所以即转换成起始节点遍历所有节点。选择DFS,是因为很契合DFS的逻辑“深度优先,递归探索。”
func canVisitAllRooms(rooms [][]int) bool {visited := make([]bool,len(rooms))var dfs func(key int)dfs = func(key int){if visited[key]{return}visited[key] = truefor _,i := range rooms[key]{dfs(i)}}dfs(0)for i := range visited{if visited[i] == false{return false}}return true
}B.并查集
并查集主要有两个功能:
- 将两个元素添加到一个集合中。
- 判断两个元素在不在同一个集合

并查集模板
package mainimport ("fmt"
)const MaxNodes = 101var n int
var father [MaxNodes]int// 初始化并查集
func initialize() {for i := 1; i <= n; i++ {father[i] = i}
}// 并查集里寻根的过程
func find(u int) int {if u == father[u] {return u}father[u] = find(father[u])return father[u]
}// 判断 u 和 v 是否找到同一个根
func isSame(u, v int) bool {return find(u) == find(v)
}// 将 v->u 这条边加入并查集
func join(u, v int) {rootU := find(u)rootV := find(v)if rootU != rootV {father[rootV] = rootU}
}func main() {var m, s, t, source, destination intfmt.Scan(&n, &m)initialize()for i := 0; i < m; i++ {fmt.Scan(&s, &t)join(s, t)}fmt.Scan(&source, &destination)if isSame(source, destination) {fmt.Println(1)} else {fmt.Println(0)}
}
1.冗余连接
方法一深搜:每遍历一条边的时候,比如[u,v],首先判断u是否能与v连通。如果不能,将其放入连通表中。如果可以连通,那就把那条边返回。对于深搜的思路:比如判断2和3能不能连通。遍历2的连通表,比如数字是1.然后接着就去判断1和3的连通性了。如果在1的连通表的可以找到3,那么就说明2,3连通。然后递归返回。
func findRedundantConnection(edges [][]int) []int {graph := make(map[int][]int)visited := make(map[int]bool)var dfs func(u, v int) booldfs = func(u, v int) bool {if u == v {return true}visited[u] = truefor _, next := range graph[u] {if !visited[next] {// 关键修复:如果递归找到路径,立即返回trueif dfs(next, v) {return true}}}return false}for _, edge := range edges {u, v := edge[0], edge[1]// 重置访问标记for node := range visited {visited[node] = false}if dfs(u, v) {return []int{u, v}}// 将当前边加入图中graph[u] = append(graph[u], v)graph[v] = append(graph[v], u)}return []int{}
}方法二:并查集:
首先记住并查集的初始化方式,还有find函数的思想。然后就一次遍历边集的,然后查看x和y是否有同一个根节点。如果有了,就证明再加那条边就冗余了。
func findRedundantConnection(edges [][]int) []int {parent := make([]int,len(edges) + 1)// 初始化并查集,每个节点的父节点指向自己for i := 1;i <= len(edges);i++{parent[i] = i}// 查找根节点(带路径压缩)var find func(int) intfind = func(x int) int {if parent[x] != x {parent[x] = find(parent[x]) // 路径压缩}return parent[x]
//处理当前逻辑:对于parent[x]通过若干的递归和回溯,已经找到了目前他所对应的根节点了。所以直接返回}for _,edge := range edges{u,v := edge[0],edge[1]rootU := find(u)rootV := find(v)if rootU == rootV{return edge}parent[rootV] = rootU}return nil
}处理当前层逻辑:在递归调用返回后,利用返回的结果来完成当前层需要完成的任务。
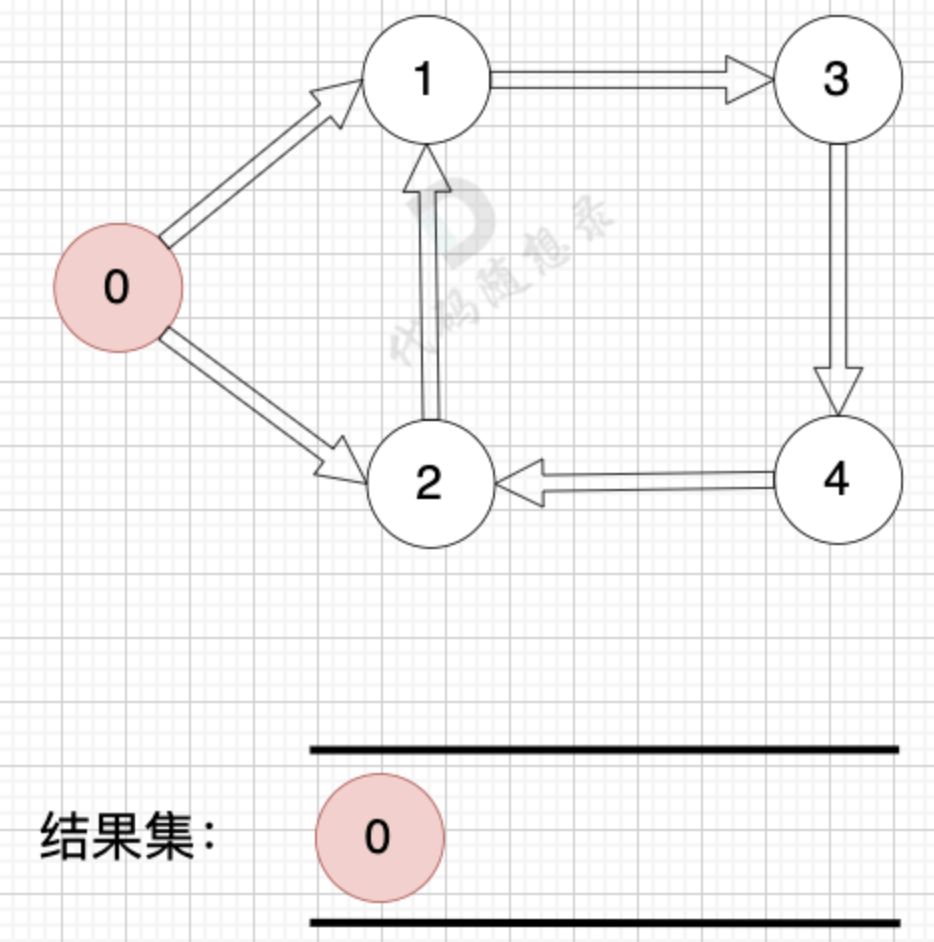
拓扑排序的过程
- 找到入度为0 的节点,加入结果集
- 将该节点从图中移除
循环以上两步,直到 所有节点都在图中被移除了。结果集的顺序,就是我们想要的拓扑排序顺序
拓扑排序判断有没有环:0加入到结果集之后,找不到入度为0的点
C.最小生成树理论
prim && kruskal
感觉面试不怎么考。。。
D.拓扑排序
拓扑排序指的是一种 解决问题的大体思路, 而具体算法,可能是广搜也可能是深搜。
1.课程表
func canFinish(numCourses int, prerequisites [][]int) bool {inDegree := make([]int,numCourses)//入度graph := make([][]int,numCourses)//邻接表for _,pre := range prerequisites{//初始化course,precourse := pre[0],pre[1]graph[precourse] = append(graph[precourse],course)inDegree[course]++}queue := []int{}for i := 0;i < numCourses;i++{//入度为0点点加入队列if inDegree[i] == 0{queue = append(queue,i)}}count := 0for len(queue) > 0{cur := queue[0]queue = queue[1:]count++// 遍历当前课程的所有后续课程for _,nextCourse := range graph[cur]{inDegree[nextCourse]--if inDegree[nextCourse] == 0{queue = append(queue,nextCourse)}}}return count == numCourses
}2.课程表2️⃣
方法一:开两个数组(冗余)方法二:
func findOrder(numCourses int, prerequisites [][]int) []int {inDegree := make([]int, numCourses)graph := make(map[int][]int)for _, val := range prerequisites {course, precourse := val[0], val[1]inDegree[course]++graph[precourse] = append(graph[precourse], course)}res := []int{}// 第一轮:添加所有入度为0的课程for i := 0; i < numCourses; i++ {if inDegree[i] == 0 {res = append(res, i)}}// 使用res作为队列,i作为指针for i := 0; i < len(res); i++ {cur := res[i]for _, next := range graph[cur] {inDegree[next]--if inDegree[next] == 0 {res = append(res, next)}}}if len(res) != numCourses {return []int{}}return res
}感悟:这也太优雅了吧。len(res) 在循环过程中会不断增长。res同时充当结果容器去存储结果,同时i也相当于指针去标记当前处理的位置
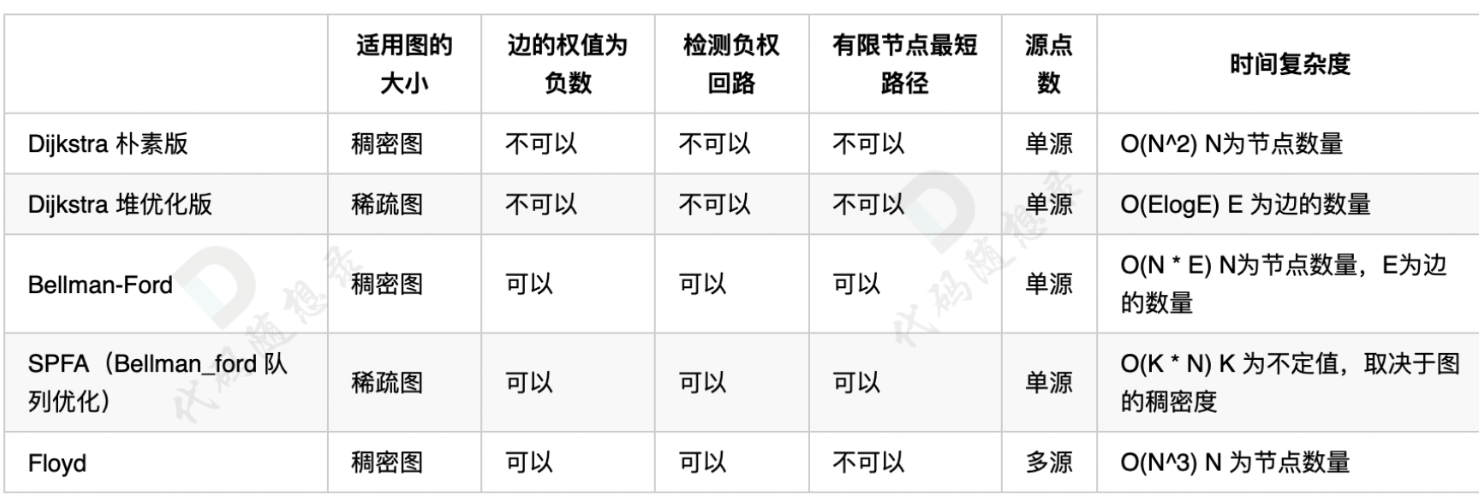
E.最短路算法理论
感觉面试不怎么考。。。




![[从青铜到王者] Spring Boot+Redis+Kafka电商场景面试全解析](http://pic.xiahunao.cn/[从青铜到王者] Spring Boot+Redis+Kafka电商场景面试全解析)






:刨根问底鸢尾花分类中的参数推理计算)







