影响含量均一性的显著因子(%RSD)
数据分析表明含量均一性的弯曲性不显著。如半正态图(图12)所示,影响含量均一性的显著因子为A(原料药粒径)和C(MCC/Lactose)。
mod2 <- lm( y3 ~A+B+C, data = study1)
anova(mod2)
Analysis of Variance Table
Response: y3
Df Sum Sq Mean Sq F value Pr(>F)
A 1 2.31125 2.31125 25.7908 0.007088 **
B 1 0.03125 0.03125 0.3487 0.586593
C 1 1.40779 1.40779 15.7092 0.016629 *
Residuals 4 0.35846 0.08962
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
with(study1, (interaction.plot(A,B,y3, type = "b", pch = c(18,24,22), leg.bty = "o", main = "Interaction Plot of A and B", xlab = "A",ylab = "y3")))
library(daewr)
fullnormal(coef(mod2)[-1], alpha=.025)
effects <-coef(mod2)
effects <-effects[2:4]
effects <-effects[ !is.na(effects) ]
halfnorm(effects, names(effects), alpha=.25)
library(BsMD)
LenthPlot(mod2, main = "Lenth Plot of Effects")

#以下将因子变量转为自然变量
A.num <-study1$A
levels(A.num) <- c(10,30)
B.num <- study1$B
levels(B.num) <- c(1,5)
A.num <- as.numeric(as.character(A.num))
B.num <- as.numeric(as.character(B.num))
mod2 <- lm( y3 ~A.num*B.num, data = study1)
contour(mod2, ~ A.num + B.num)
persp(mod2, ~ A.num + B.num, zlab=" y3", contours=list(z="bottom"))


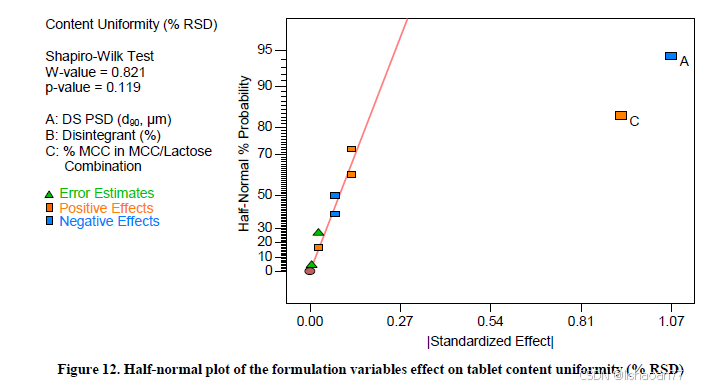
图13展示原粒药粒径和MCC/Lactose对含量均一性的影响。

影响粉末流动性的显著性因子
如半正态图(图14)所示,显著因子是A,C。图15展示原料粒径以及MCC/Lactose对流动性的影响。
mod3 <- lm( y5 ~A+B+C, data = study1)
anova(mod3)
Analysis of Variance Table
Response: y5
Df Sum Sq Mean Sq F value Pr(>F)
A 1 11.8584 11.8584 51.7241 0.00198 **
B 1 0.0421 0.0421 0.1834 0.69051
C 1 1.7994 1.7994 7.8488 0.04873 *
Residuals 4 0.9171 0.2293
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
with(study1, (interaction.plot(A,B,y5, type = "b", pch = c(18,24,22), leg.bty = "o", main = "Interaction Plot of A and B", xlab = "A",ylab = "y1")))
library(daewr)
fullnormal(coef(mod3)[-1], alpha=.025)
effects <-coef(mod3)
effects <-effects[2:4]
effects <-effects[ !is.na(effects) ]
library(daewr)
halfnorm(effects, names(effects), alpha=.25)
library(BsMD)
LenthPlot(mod3, main = "Lenth Plot of Effects")
#以下将因子变量转为自然变量
A.num <-study1$A
levels(A.num) <- c(10,30)
B.num <- study1$B
levels(B.num) <- c(1,5)
A.num <- as.numeric(as.character(A.num))
B.num <- as.numeric(as.character(B.num))
mod3 <- lm( y5 ~A.num*B.num, data = study1)
contour(mod3, ~ A.num + B.num)
persp(mod3, ~ A.num + B.num, zlab=" y1", contours=list(z="bottom"))





影响片剂硬度的显著因子
每个批次均用5 kN, 10 kN 和15 kN力压片以评估可压片性。图16半正态图显示10 kN时只有MCC/Lactose影响片剂硬度。5 kN和15 kN可以得到相似的关系(不在此提供数据)。图17展示MCC/Lactose对片剂硬度的影响。
mod4 <- lm( y7 ~A+B+C, data = study1)
anova(mod4)
Analysis of Variance Table
Response: y7
Df Sum Sq Mean Sq F value Pr(>F)
A 1 0.845 0.8450 0.1628 0.7072
B 1 2.205 2.2050 0.4249 0.5500
C 1 13.450 13.4496 2.5920 0.1827
Residuals 4 20.755 5.1888
with(study1, (interaction.plot(A,B,y7, type = "b", pch = c(18,24,22), leg.bty = "o", main = "Interaction Plot of A and B", xlab = "A",ylab = "y7")))
library(daewr)
fullnormal(coef(mod4)[-1], alpha=.025)
effects <-coef(mod4)
effects <-effects[2:4]
effects <-effects[ !is.na(effects) ]
halfnorm(effects, names(effects), alpha=.25)
library(BsMD)
LenthPlot(mod4, main = "Lenth Plot of Effects")
#以下将因子变量转为自然变量
A.num <-study1$A
levels(A.num) <- c(10,30)
B.num <- study1$B
levels(B.num) <- c(1,5)
A.num <- as.numeric(as.character(A.num))
B.num <- as.numeric(as.character(B.num))
mod4 <- lm( y7 ~A.num*B.num, data = study1)
contour(mod4, ~ A.num + B.num)
persp(mod4, ~ A.num + B.num, zlab=" y7", contours=list(z="bottom"))





影响片剂脆碎度的显著因子
5 kN, 10 kN and 15 kN 压片的脆碎度都很好,没有的显著影响脆碎度的因子。
影响片剂稳定性的因子
所有的批次均放在40°C/75% RH的稳定性研究箱里时行研究。没有因子显著影响降解产物。
处方研究1的总结
Acetriptan的粒径分布显著影响片剂溶出度,含量均一性,粉末流动性。小的粒径分布可以增加溶出度,但是对含量均一性和流动性有负的影响。
崩解剂的用量显著影响片剂的溶出度因为它与原料粒径分布有交互作用。当粒径分布大时崩解剂对溶出的影响更大。
MCC/Lactose比例显著影响粉末流动性,含量均一性和片剂硬度。增加MCC的比例将增加片剂硬度但是降低粉末流动性和负面影响含量均一性。为了平衡流动性和片剂硬度,最终处方选择50%MCC/Lactose。
因为多个响应均没有显著的二次效应,全因子DOE可以识别所有的主效应和交互作用而没有别名项。没有必要时一步研究优化颗粒内辅料。变些DOE模型可以建立处方变量的可接受范围。图18展示所有响应的叠加图。绿色的区域表示所有的响应可以同时实现。

为了适应尽大可能的粒径分布并避免溶出失败的可能性,选择 5% of croscarmellose sodium 作为最终处方。当选 择这种用量的时候,原粒药的d90 是 14-30 μm。d90 小于 14 μm 时流动性差导致不可接受的片剂含量均一性当生产工艺固定时。因此时一步研究原料的粒径分布。
为了研究原料粒径对体外性能的影响并识别生物等效的粒径上限,在中试规模研究d90 为 20 μm, 30 μm 和45 μm (对应于 d50 为 12 μm, 24 μm 和39 μm)。
到研究1结束时的处方见表25。
















:BeautifulSoup库)

)

