入门
久闻并查集的大名,今天来一探究竟,到底什么是并查集,并查集有什么用?
并查集(Disjoint Set Union, DSU)是一种处理不相交集合的合并及查询问题的数据结构。
其实并查集的作用主要就有两个:
1、将两个元素添加到同一个集合
2、判断两个元素是否在同一个集合内
碰到诸如此类的问题,就可以条件反射的去想到用并查集来解决了。
首先就是预处理的操作了只需要将所有的点连向自己即可:
void pre_handle()
{for(int i=0;i<n;i++) father[i] = i;
} 然后就是添加函数和判断函数了,这两个函数都基于查找函数,要首先查找到两个点的根节点是谁
普通的查找函数:查找函数是基于递归来实现的,就是不断的递归去找父节点的父节点知道根节点
int find(int x)
{if(father[x] == x) return x;return find(father[x]);
}但是这样一直递归无疑是一个非常浪费时间的过程,每次查找一个点的根节点的时候都要从这个点开始递归到根节点,其实这个过程中做了很多重复的东西,在一个点递归完之后,他的所有父节点是不就就无需再递归了呢,所以就要考虑能不能把路径压缩,其实只需要在递归的过程中,将每个点的父节点都存为根节点,这样在下一次查找的时候,既可以直接根据这个点存的值直接找到该点的根节点了,比如一开始的1->2->3->4 当find(1)的时候在递归的过程中就变为了1->4, 2->4, 3->4 这样在下一次找2的根节点的时候就直接递归一次即可返回4,这个操作在较深的图中是很有用的!
int find(int x)
{if(father[x] == x) return x;father[x] = find(father[x]);//直接将根节点赋值给x的父节点 相当于深度变为了两层return father[x];
}这样是不是很妙呢?有了find函数,接下来的添加(join)和判断(is_same)函数就很容易实现了。
join:
void join(int x,int y)
{x = find(x);//x直接存x的根节点y = find(y);//y同样存y的根节点if(x==y) return ;//如果x和y的根节点相同就说明本来就在同一个集合内father[x] = y;//让x的根节点指向y的根节点 就说明此时两个集合已经联通了
}is_same:
bool is_same(int x,int y)
{x = find(x);y = find(y);return x==y ? true : false;
}理论完成,下面开始做几道题来练练手吧!
寻找存在的路径
题目链接:寻找存在的路径
这是并查集的基础模板的应用,按要求将联通的两个点加入到同一个集合中即可。
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define pii pair<int,int>
#define fi first
#define se second
const int N = 110;
vector<int> father(N);
int n,m;
void pre_handle()
{for(int i=1;i<=n;i++) father[i] = i;
}
int find(int x)
{if(x == father[x]) return x;father[x] = find(father[x]);return father[x];
}
void join(int x,int y)
{x = find(x);y = find(y);if(x == y) return ;father[x] = y;//两个集合联通
}
bool is(int x,int y)
{x = find(x);y = find(y);return x==y ? true : false;
}
void solve()
{cin>>n>>m;pre_handle();for(int i=1;i<=m;i++){int u,v;cin>>u>>v;join(u,v);}int u,v;cin>>u>>v;if(is(u,v)) cout<<"1"<<endl;else cout<<"0"<<endl;
}signed main()
{IOSint T=1;
// cin>>T;while(T--) solve(); return 0;
}
冗余的边
题目链接:冗余的边
这道题虽然是看着像一个复杂的树或图问题,其实本质上就是判断当前的边所连接的两个点之前可达不可达,如果可达(联通)的话那么此时的边就是冗余的了,又因为联通无环无向图就是一颗树所以只有一条冗余的边。那么只需要用并查集去判断是否可达(在一个集合内)即可。
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define pii pair<int,int>
#define fi first
#define se second
const int N = 1010;
vector<int> father(N);
int n;
int ans1,ans2;
void pre_handle()
{for(int i=1;i<=n;i++) father[i] = i;
}
int find(int x)
{if(x == father[x]) return x;father[x] = find(father[x]);return father[x];
}
void join(int x,int y)
{x = find(x);y = find(y);if(x == y) return ;father[x] = y;//两个集合联通
}
bool is(int x,int y)
{x = find(x);y = find(y);return x==y ? true : false;
}
void solve()
{cin>>n;pre_handle();for(int i=1;i<=n;i++){int u,v;cin>>u>>v;if(is(u,v))//只要u和v在同一个集合中(可达 联通)就说明此时的边冗余了{ans1 = u;ans2 = v;}else join(u,v);}cout<<ans1<<" "<<ans2<<endl;
}signed main()
{IOSint T=1;
// cin>>T;while(T--) solve(); return 0;
}
冗余的边II
题目链接:冗余的边II
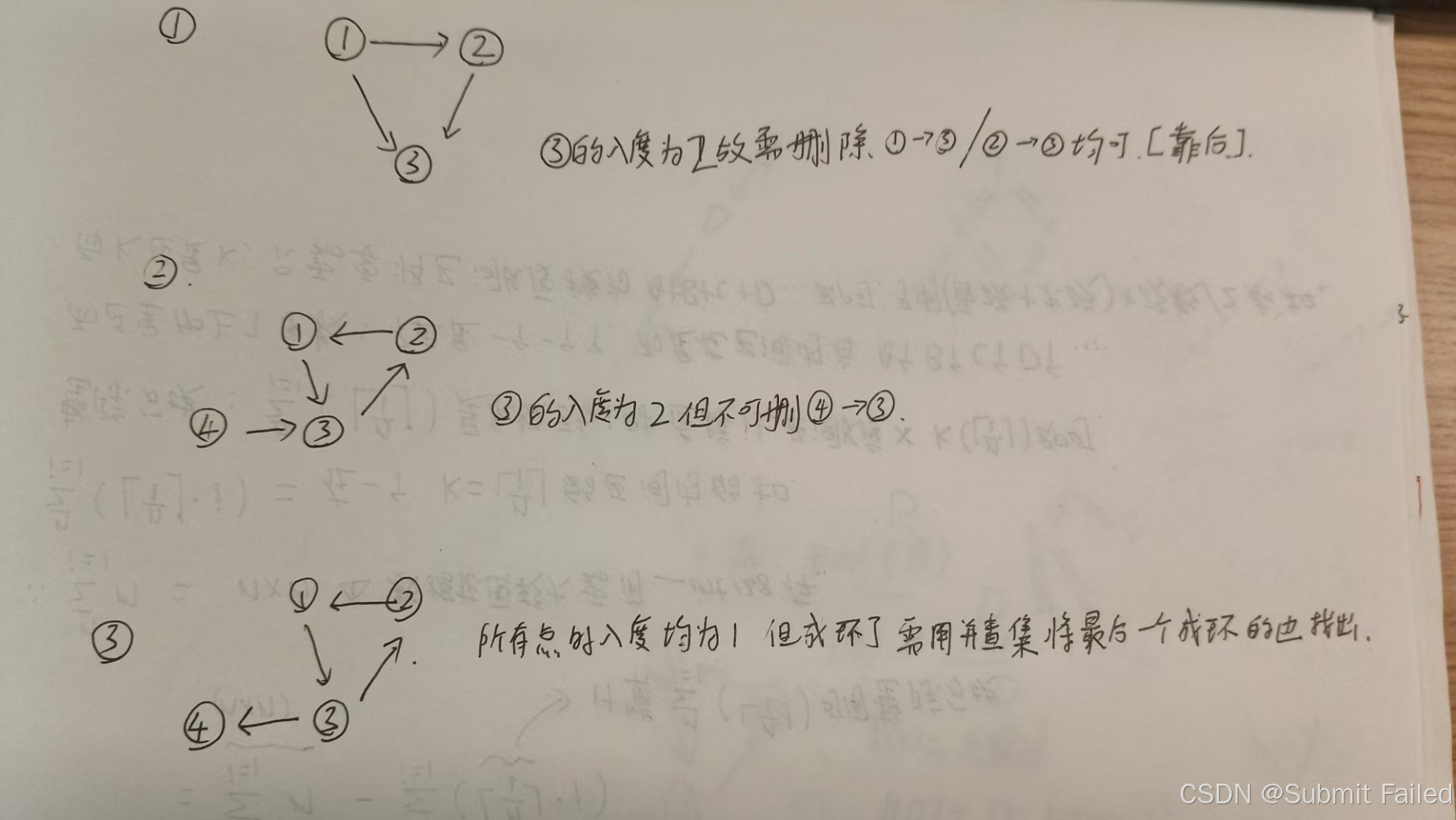
这道题原本是一个有向树,因为多了一条冗余的边导致成为了一个图,所以我们就要判断哪些情况是导致冗余的原因,大体上分为两种
1.有向树的性质就是除了根节点的入度为0,其他的节点入度为1,入度为2就说明不是树了
2.入度也可能都是1,但是如果构成环了也就不是树了
但是第一种情况又可以细分,入度为2可能只有其中一条边是冗余的(入度为0的根节点与其相连的时候 这条边就不是一个冗余的边)所以要在入度为2的时候判断一下是否能删
可以利用并查集来判断是否有环!
题目特殊条件:
图是由"有向树添加一条边"构成的
这意味着原始结构是一棵有向树(n-1条边)
添加一条边后(共n条边),只可能产生两种违规情况:
a) 某个节点入度变为2
b) 形成一个环并查集的适用性:
虽然并查集通常用于无向图,但这里我们关注的是"连接性"而非方向
判断是否有环时,方向不重要(有向环必然包含无向环)
判断连通性时,方向也不重要(我们只需知道节点是否相连)
方向信息的处理:
入度统计单独处理(用
indegree数组)并查集只负责检测环和连通性
两个部分各司其职,共同解决问题
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define pii pair<int,int>
#define fi first
#define se second
const int N = 1010;
vector<int> father(N),indegree(N,0),a;//定义并查集数组 入度数组 以及入度为2的数组
vector<pii> e(1);//存所有的两两有连接的边 不需要建树 只需要用入度和并查集统计边即可
int n;
void init()//初始化并查集
{for(int i=1;i<=n;i++) father[i] = i;
}
int find(int x)
{if(x == father[x]) return x;return father[x] = find(father[x]);
}
void join(int x,int y)
{x = find(x);y = find(y);if(x == y) return ;father[x] = y;
}
bool is(int x,int y)
{x = find(x);y = find(y);return x==y ? true : false;
}
bool istree(int x)//删除x这条边之后是否是一棵树
{//判断连通性时,方向并不重要(我们只需知道节点是否相连)init();for(int i=1;i<=n;i++){if(i == x) continue;if(is(e[i].fi,e[i].se)) return false;//成环了 不是有向树了join(e[i].fi,e[i].se);}return true;
}
void solve()
{cin>>n;init();for(int i=1;i<=n;i++){int u,v;cin>>u>>v;e.push_back({u,v});indegree[v]++;}for(int i=1;i<=n;i++){if(indegree[e[i].se] == 2) a.push_back(i);//将导致入度为2的边的编号存入}if(a.size()>0)//size==2{if(istree(a[1]))//因为要输出标准输入中靠后的一个 所以先判断a[1]cout<<e[a[1]].fi<<' '<<e[a[1]].se<<endl;else//如果删除a[1]这条边的话还是一个图 那么就一定是另一条边了(因为只会多出来一条边)cout<<e[a[0]].fi<<' '<<e[a[0]].se<<endl;}else//第三种情况{init();//找冗余的边 用并查集 判断成环的那条边//判断是否有环时,方向并不重要(有向环必然包含无向环)for(int i=1;i<=n;i++){if(is(e[i].fi,e[i].se)){cout<<e[i].fi<<' '<<e[i].se<<endl;return ;}elsejoin(e[i].fi,e[i].se);}}
}signed main()
{IOSint T=1;
// cin>>T;while(T--) solve(); return 0;
}
总之,并查集应用于无向图中,目的是看两个点是否联通或者两个集合是否联通以及将两个点加入到同一个集合当中构成联通性。
这样就将并查集的两个主要作用给介绍完了,期待后续的迪杰斯特拉算法吧!

















)
和邮箱(Email)的特定弹窗)
