题意：给出一个圆，顺时针排布1~2*n，已知连了k条边，问这个圆最好情况下有多少个线的交点，要求线与线之间不能有重复的连接点，也就是每个点只能被一条线连接

思路：

1.考虑没有线的时候，那一定是i与i+n相连接，这一定是最多的连法

2.再考虑提前加了一条边，那么一定是由这根线分割的两边相连，但是仔细想一下当两边数量不对等的时候，少的那一边一定会连向多的一边的中间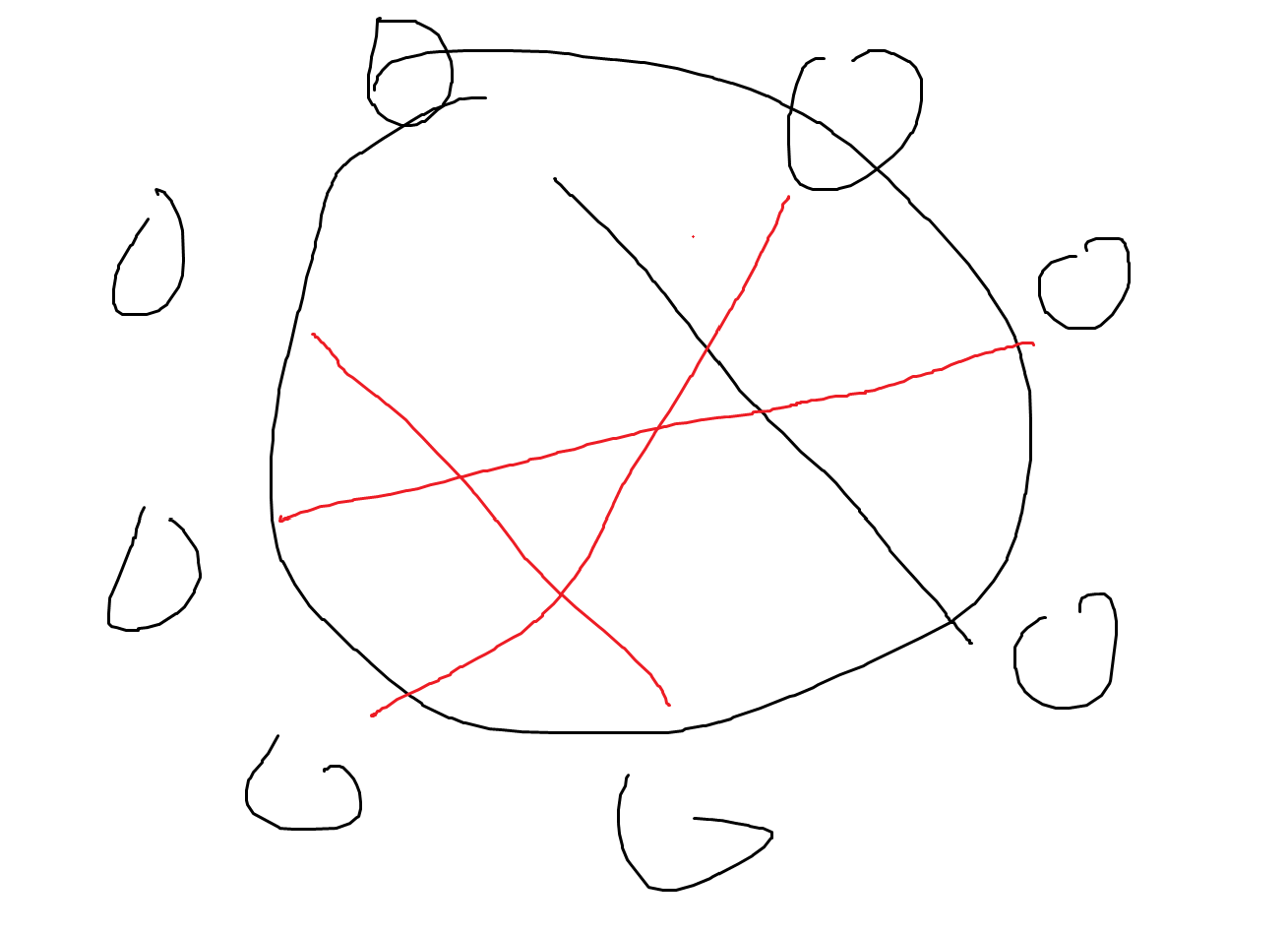

 如图，这样才是最多的，但是发现依旧是类似于i*i+n的构造方式

3.考虑继续加边，依旧会有这种感觉对吗，因为这样才会让交点的数量多起来
考虑对自己能操作的边进行交换，只会导致连的边减少
但是对已有边，不会改变性质
这是因为已有边的贡献是由min(上边和下边)决定的，单纯的选两条线改变交点，不会改变原有的两个点处于上下边的性质

 如图，所以i与i+n这种构造模式，依旧是对已有边的最佳处理
而且不会存在i与i+n在同一侧的情况,i+k(某一边的最小数量)<左侧+右侧/2，因此得证
对未填边最大的处理方式，且一定满足已有边的需求

正确性来源参考CF1552C Maximize the Intersections 题解 - 洛谷专栏

至于本人？做的时候根本没想这么多，试着试着就出来了，因为i与i+n的这种构造方式一定是对已有情况的最大，硬猜给猜出来了……

代码：
这是自己写过的代码，有点臃肿，看着数据量直接强行暴力了，实际上很多步骤可以去掉……

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define IOS                       \std::ios::sync_with_stdio(0); \std::cin.tie(0);              \std::cout.tie(0)const int N = 3e5 + 5;
const int INF = 1e18;
// const int MOD = 998244353;
// const int MOD=1e9+7;
// const int MOD=100003;
const int maxn=5e5+10;void solve(){int n,k;std::cin >> n >> k;std::vector<int> bz(2*(n+1));int cnt=n+1;std::vector<int> rec; for(int i=0;i<k;i++){int x,y;std::cin >> x >> y;int z=0;bz[x]=y;bz[y]=x;}int res=0;for(int p=1;p<=2*n;p++){std::vector<int> in,out;int now=0;int cnt=0;int i=p;while(cnt<2*n){if(!bz[i]){in.push_back(i);}i++;if(i==2*n+1) i=1;cnt++;}cnt=0;i=p;while(cnt<2*n){if(!bz[i]){out.push_back(i);}i--;if(i==0) i=2*n;cnt++;}for(int i=0,j=0;j<out.size()/2;i++,j++){bz[in[i]]=in[i+out.size()/2];bz[in[i+out.size()/2]]=in[i];}for(int i=1;i<=2*n;i++){if(bz[i]<i) continue;int nex=bz[i];for(int j=i+1;j<=bz[i];j++){if(bz[j]>bz[i]) now++;}}res=std::max(now,res);for(auto i : in){bz[i]=0;}}std::cout << res << '\n';}  signed main(){IOS;int t=1;std::cin >> t;while(t--){solve();}
}