Java 排序

文章目录

  • 排序
    • 插入排序
      • 分析
    • 希尔排序
      • 分析
    • 选择排序
      • 分析
    • 堆排序
      • 分析
    • 冒泡排序
      • 分析
    • 快速排序
      • 霍尔法
      • 分析
      • 挖坑法找基准
      • 前后指针法
      • 题目
      • 快排的优化
        • 三数取中法
      • 非递归实现快排
    • 归并排序
      • 分析
      • 非递归实现归并排序
    • 海量数据的排序
    • 非比较的排序
      • 计数排序
      • 分析
      • 基数排序
      • 桶排序

在这里插入图片描述

排序

  1. 稳定的排序：排序之前和排序之后它们俩的相对顺序没有发生变化
  2. 内部排序：在内存上的排序
  3. 外部排序：需要借助磁盘等外部空间进行的排序

插入排序

  1. 思想：假设这组数据的第一个元素是有序的，从第二个元素和前面的元素进行比较，找到合适的位置进行插入

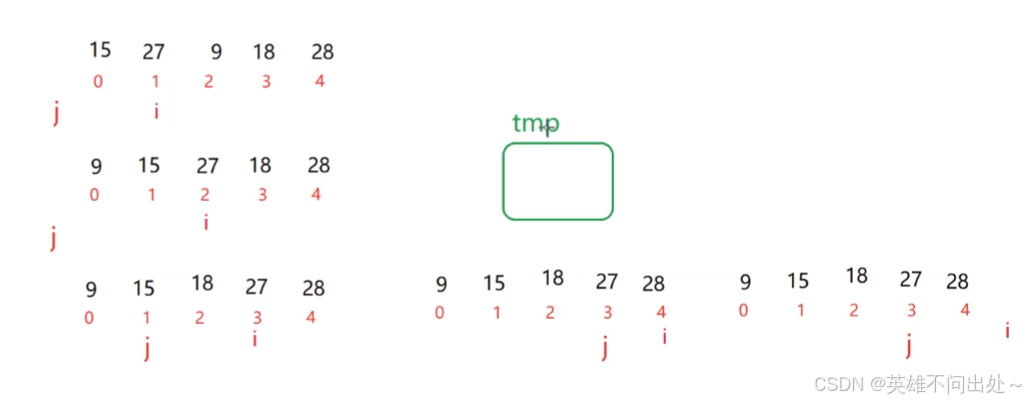
在这里插入图片描述

// 插入排序public static void insertSort(int[] array){for(int i = 1;i < array.length;i++){int j = i - 1;int tmp = array[i];for(;j >= 0;j--){if(array[j] > tmp){array[j+1] = array[j];}else{break;}}array[j + 1] = tmp;}}

分析

  1. 时间复杂度：O(N^2)
    最坏情况：O(N^2)
    最好情况：有序的数组，O(N)
    数据越有序，排序越快
    适用于待排序数组基本上趋于有序了，时间复杂度趋于O(N)
  2. 空间复杂度：O(1)
  3. 稳定性：是一个稳定的排序
    例子：5 5 7
    稳定的排序可以改成不稳定的排序，但是不稳定的排序不能改成稳定的排序

希尔排序

  1. 对直接插入排序进行了优化，如果是 5 4 3 2 1 会退化为O(N^2)
  2. 分组：分完组后，每组都采用直接插入排序
  3. 中间隔一些元素进行分组的好处：比较大的元素都往后走了，比较小的元素都往前走了
  4. 缩小增量到最后会把整体看成是一组，5 3 1 组，前面的5 3 都是预排序，真正的排序是最后的一组
  5. 缩小增量的目的：为了让排序更接近O(N)，为了让排序更快

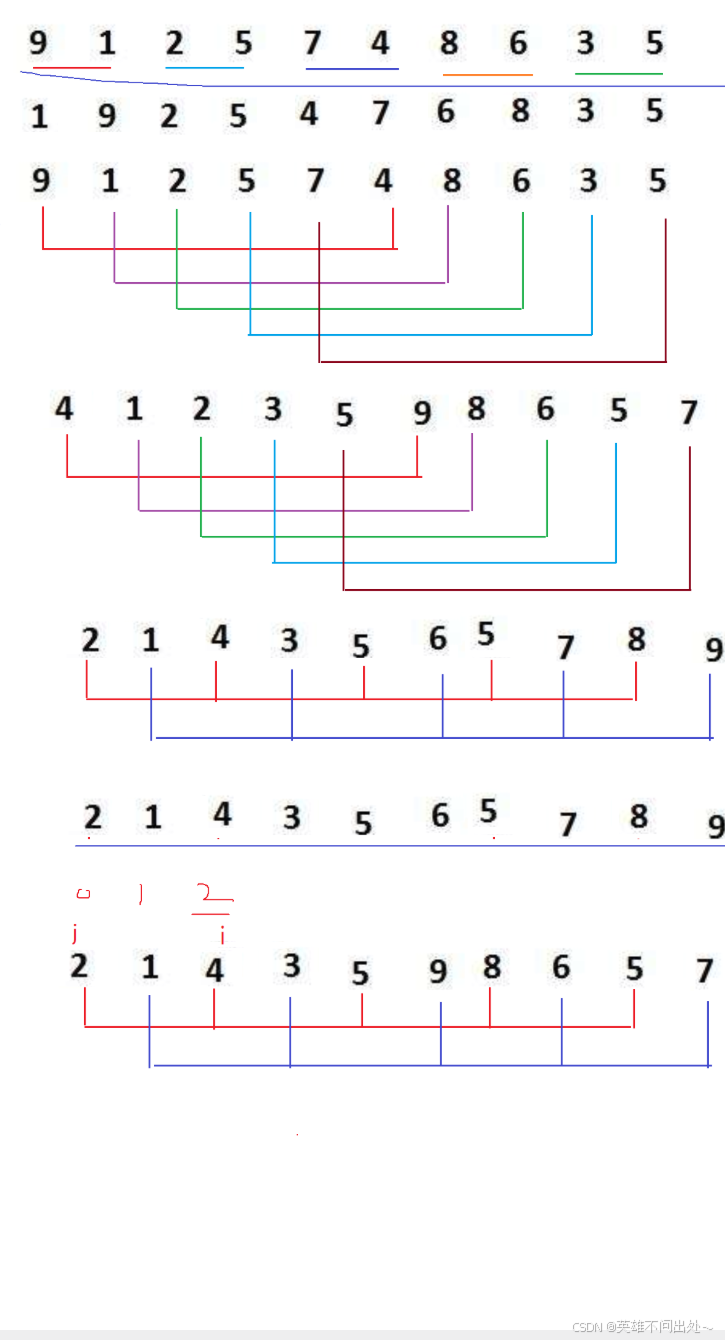
在这里插入图片描述
在这里插入图片描述

// 希尔排序public static void shellSort(int[] array){int gap = array.length;while(gap > 1){gap /= 2;shell(array,gap);}}// 对每组进行插入排序public static void shell(int[] array,int gap){for(int i = gap;i < array.length;i++){int j = i - gap;int tmp = array[i];for(;j >= 0;j -= gap){if(array[j] > tmp){array[j+gap] = array[j];}else{break;}}array[j + gap] = tmp;}}

分析

  1. 时间复杂度：O(N^1.3 - N ^ 1.5)，时间复杂度不好计算
  2. 空间复杂度：O(1)
  3. 稳定性：不稳定的排序

检测排序速度：

public static void testInsert(int[] array){long startTime = System.currentTimeMillis();int[] tmp = Arrays.copyOf(array,array.length);Sort.insertSort(tmp);long endTime = System.currentTimeMillis();System.out.println(" " + (endTime - startTime));}public static void testShell(int[] array){long startTime = System.currentTimeMillis();int[] tmp = Arrays.copyOf(array,array.length);Sort.shellSort(tmp);long endTime = System.currentTimeMillis();System.out.println(" " + (endTime - startTime));}// 逆序初始化public static void initOrder(int[] array){for(int i = 0;i < array.length;i++){array[i] = array.length - i;}}public static void main(String[] args) {int[] arr = new int[10000];initOrder(arr);testInsert(arr);testShell(arr);}

选择排序

  1. 在当前i下标对应的值的后面，找到后面最小的值和i下标对应的值交换
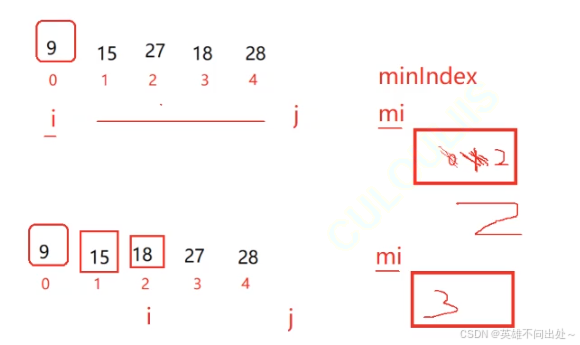
	// 交换public static void swap(int i, int j, int[] array){int tmp = array[i];array[i] = array[j];array[j] = tmp;}// 选择排序public static void selectSort(int[] array){// 在i下标的后面找到比i下标对应的值的最小值,然后交换int n = array.length;for(int i = 0;i < n;i++){int minIndex = i;for(int j = i + 1;j < n;j++){if(array[j] < array[i]){if(array[j] < array[minIndex]){minIndex = j;}}}swap(i,minIndex,array);}}
  1. 双向选择排序
    时间复杂度还是O(N^2)
    左边找最大的，右边找最小的，和第一个数和最后一个数交换
    在这里插入图片描述
    存在缺陷，maxIndex下标可能是在0下标是最大的，0下标会和最小值小标的值交换，那么0下标就不是最大值下标，应该更新为maxIndex = minIndex

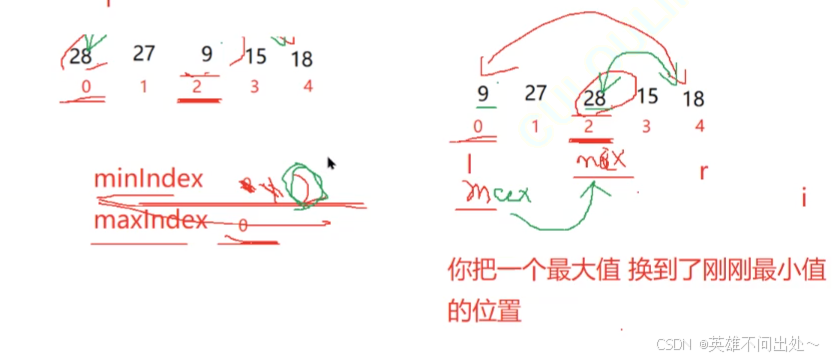
在这里插入图片描述

public static void selectSort2(int[] array){// 在i下标的后面找到比i下标对应的值的最小值,然后交换int left = 0;int right = array.length - 1;while(left < right){int minIndex = left;int maxIndex = left;for(int i = left + 1;i <= right;i++){if(array[i] < array[minIndex]){minIndex = i;}if(array[i] > array[maxIndex]){maxIndex = i;}}swap(left,minIndex,array);// 第一个数是最大的数,防止最小的下标和第一个数换了,最大值就在minIndex的位置了if(maxIndex == left){maxIndex = minIndex;}swap(right,maxIndex,array);left++;right--;}}

分析

  1. 时间复杂度：O(N^2)
  2. 空间复杂度：O(1)
  3. 稳定性：不稳定的排序

堆排序

// 堆排序private static void shifDown(int[] array,int parent,int len){int child = 2 * parent + 1;while(child < len){if(child + 1 < len && array[child] < array[child + 1]){child++;}if(array[child] > array[parent]){swap(child,parent,array);parent = child;child = 2 * parent + 1;}else{break;}}}private static void createHeap(int[] array){// 建立大根堆for(int parent = (array.length - 1 - 1) / 2;parent >= 0;parent--) {shifDown(array, parent, array.length);}}public static void heapSort(int[] array){createHeap(array);int end = array.length - 1;while(end > 0){swap(end,0,array);shifDown(array,0,end);end--;}}

分析

  1. 时间复杂度：O(N * logN)
  2. 空间复杂度：O(1)
  3. 稳定性：不稳定的排序

冒泡排序

// 冒泡排序public static void bubbleSort(int[] array){// i是趟数for(int i = 0;i < array.length;i++){// j是比较的大小的boolean flag = true;for(int j = 0;j < array.length - i - 1;j++){if(array[j] > array[j + 1]){swap(j,j + 1,array);flag = false;}}if(flag) {break;}}}

分析

  1. 时间复杂度：O(N ^ 2)
  2. 空间复杂度：O(1)
  3. 稳定性：稳定的排序

快速排序

霍尔法

  1. 根据二叉树进行递归划分

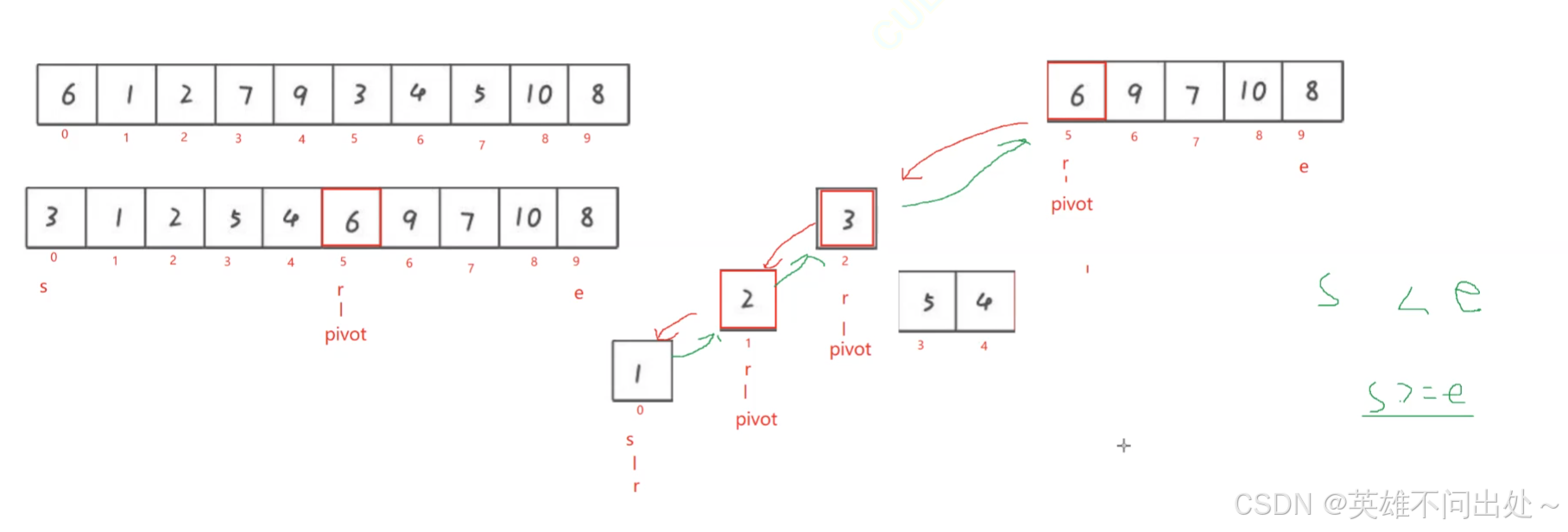
在这里插入图片描述

// 快速排序public static void quickSort(int[] array){quick(array,0,array.length - 1);}private static void quick(int[] array,int start,int end){if(start >= end){return;}int prvot = partitionHoare(array,start,end);quick(array,start,prvot - 1);quick(array,prvot + 1,end);}private static int partitionHoare(int[] array,int left,int right){// 基准元素int tmp = array[left];// 记录第一个基准下标int i = left;while(left < right) {// 必须先找先右再左// 找小while (left < right && array[right] >= tmp) {right--;}// 找大while (left < right && array[left] <= tmp) {left++;}swap(left, right, array);}swap(i,left,array);return left;}
  1. 为什么有等于号？
    没有等于号，会死循环，比如两端都是6

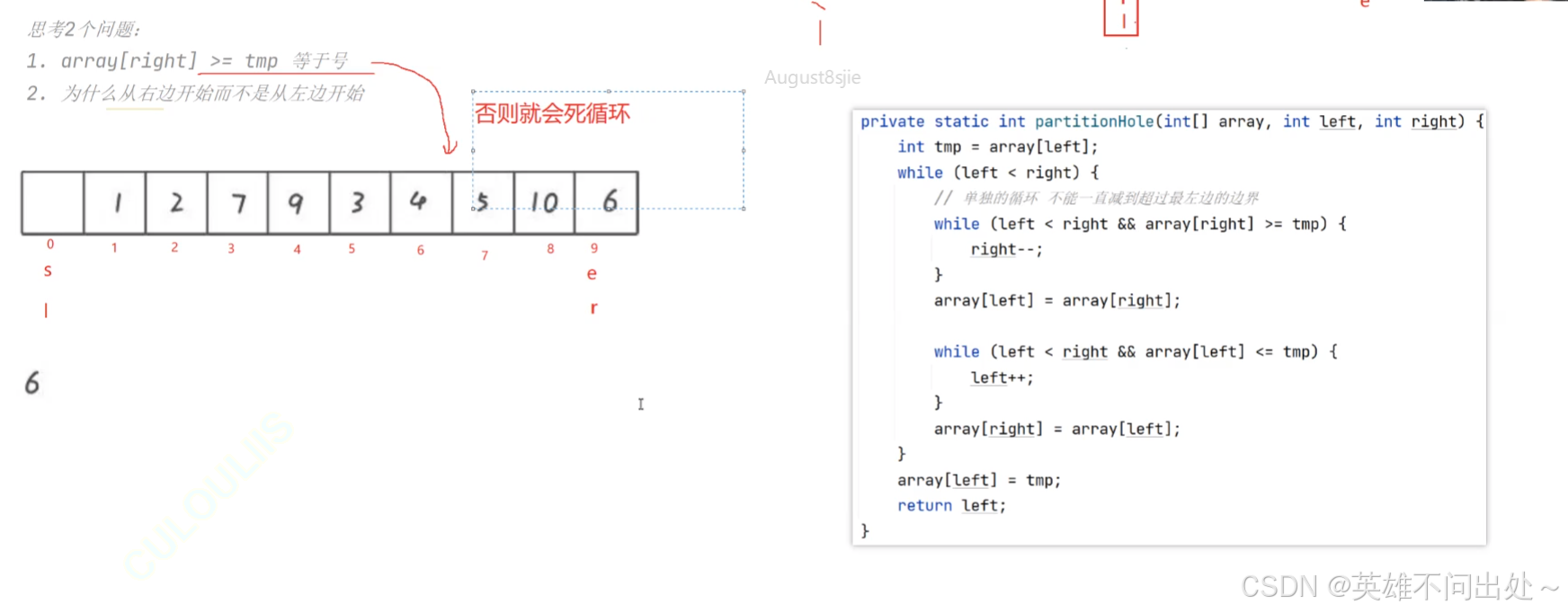
在这里插入图片描述

  1. 为什么先从右边开始，不先从左边开始？
    先走左边的话，先遇到大的停下来，如果相遇的话，那么相遇位置的值就是大于基准元素的，这时候交换的话，6的左边有一个数比6大
    在这里插入图片描述

分析

  1. 时间复杂度：
    最好情况下：O(N * logN)
    每层都有N个节点，高度为logN，需要每个节点都遍历到，N * logN次遍历
    最坏情况下：O(N^2)，有序/逆序，单分支的树
  2. 空间复杂度：
    最好情况下：O(logN)
    最坏情况下：O(N)，有序/逆序，单分支的树
    递归左边再递归右边，递归右边左边没有释放
  3. 稳定性：不稳定的排序

挖坑法找基准

  1. 先走右边再走左边，以第一个元素为基准，并且拿出基准元素，基准元素的位置就是坑，如果右边找到比基准小的，把它放入坑中，左边找到比基准元素大的放到坑中，最后两者相遇，把基准元素放入其中
// 挖坑法private static int partitionHole(int[] array,int left,int right){// 基准元素int tmp = array[left];while(left < right) {// 必须先找先右再左// 找小while (left < right && array[right] >= tmp) {right--;}array[left] = array[right];// 找大while (left < right && array[left] <= tmp) {left++;}array[right] = array[left];}array[left] = tmp;return left;}

前后指针法

  1. 如果cur比基准元素小并且cur下标的值和prev下标的值不相等，

在这里插入图片描述

// 前后指针法public static int partition(int[] array,int left,int right){int prev = left;int cur = left + 1;while(cur <= right){while(array[cur] < array[left] && array[++prev] != array[cur]){swap(cur,prev,array);}cur++;}swap(prev,left,array);return prev;}

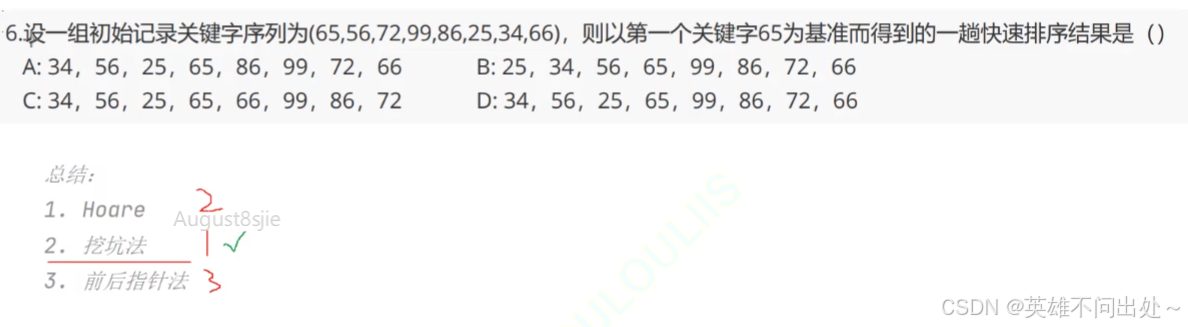
题目

  1. 优先试挖坑法，其次是Hoare，最后是前后指针法

A

在这里插入图片描述

快排的优化

  1. 均匀的分割数组
  2. 让递归的次数变少
三数取中法
  1. 三数取中法：left，right，mid三个下标中的中间值和第一个数交换位置，然后右边找比基准元素小的值，左边找比基准元素大的值
  2. 规定array[mid] <= array[left] <= array[right]
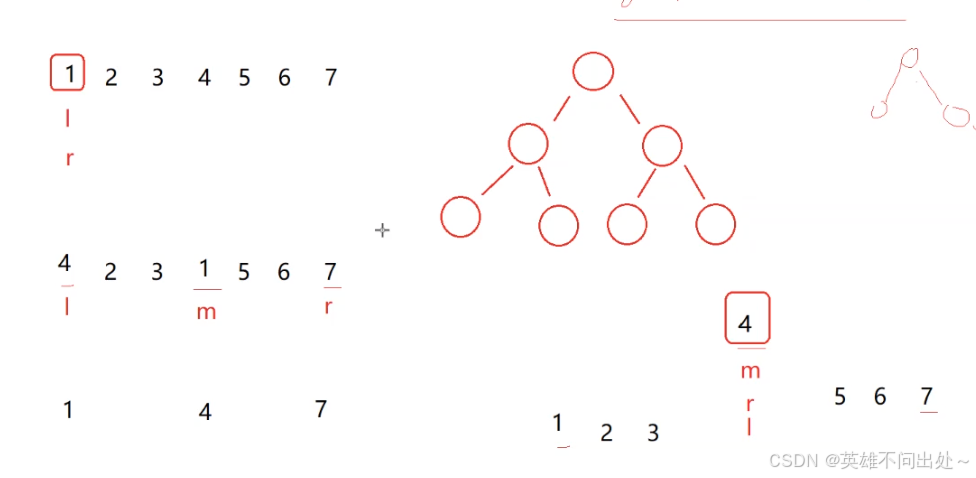
    在这里插入图片描述
// 三数取中法,求中位数的下标private static int middleNum(int[] array,int left,int right){int mid = (left + right) / 2;if(array[left] < array[right]){// 1. x < 3 < 9// 2. 3 < 9 < x// 3. 3 < x < 9if(array[mid] < array[left]){return left;}else if(array[mid] > array[right]){return right;}else{return mid;}}else{// 9 > 3 == left > right// 1. x > left > rightif(array[mid] > array[left]){return left;}else if(array[right] > array[mid]){// 2. left > right > xreturn right;}else{// 3. left > x > rightreturn mid;}}}private static void quick(int[] array,int start,int end){if(start >= end){return;}// 1 2 3 4 5 6 7// 中间值的下标和第一个数交换,作为新的基准元素int index = middleNum(array,start,end);swap(index,start,array);// 4 2 3 1 5 6 7// 为了让左右分布更均匀,降低树的高度,减少递归的次数int prvot = partition(array,start,end);quick(array,start,prvot - 1);quick(array,prvot + 1,end);}

只剩最后几层时，使用插入排序进行优化，降低递归次数，可以使用插入排序是因为前面递归成有序的序列了

public static void insertSort(int[] array,int left,int right){for(int i = left + 1;i <= right;i++){int j = i - 1;int tmp = array[i];for(;j >= left;j--){if(array[j] > tmp){array[j+1] = array[j];}else{break;}}array[j + 1] = tmp;}}private static void quick(int[] array,int start,int end){if(start >= end){return;}if(end - start + 1 <= 15){// 减少递归的次数// 因为最后几层节点数最多,递归次数也多insertSort(array,start,end);return;}// 1 2 3 4 5 6 7// 中间值的下标和第一个数交换,作为新的基准元素int index = middleNum(array,start,end);swap(index,start,array);// 4 2 3 1 5 6 7// 为了让左右分布更均匀,降低树的高度,减少递归的次数int prvot = partition(array,start,end);quick(array,start,prvot - 1);quick(array,prvot + 1,end);}

非递归实现快排

  1. 找基准里面会进行交换元素，进行排序，外面就进行找到左右下标位置

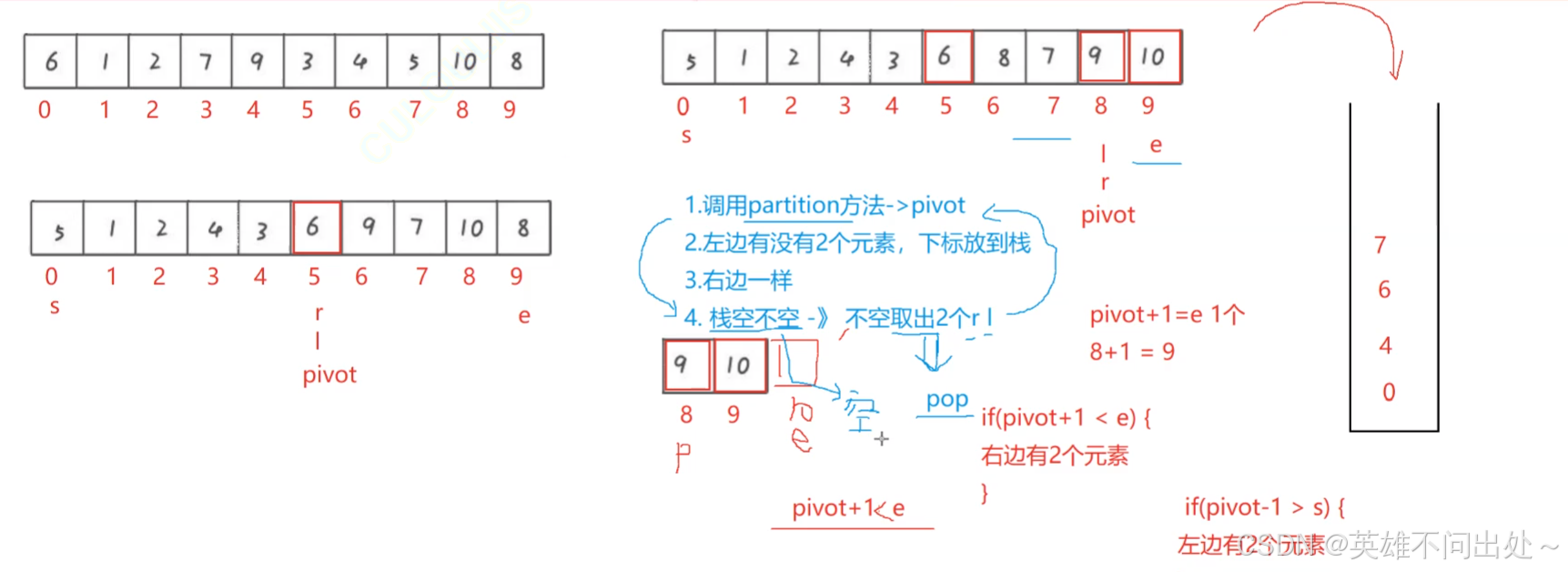
在这里插入图片描述

 // 非递归实现快速排序public static void quickSortNor(int[] array){int start = 0;int end = array.length - 1;Stack<Integer> stack = new Stack<>();int pivot = partitionHoare(array,start,end);if(pivot - 1 > start){// 左边有两个元素stack.push(start);stack.push(pivot - 1);}else if(pivot + 1 < end){// 右边至少有两个元素stack.push(pivot + 1);stack.push(end);}// 找基准里面会互换元素进行排序while(!stack.empty()){end = stack.pop();start = stack.pop();pivot = partitionHoare(array,start,end);if(pivot - 1 > start){// 左边有两个元素stack.push(start);stack.push(pivot - 1);}else if(pivot + 1 < end){// 右边至少有两个元素stack.push(pivot + 1);stack.push(end);}}

归并排序

  1. 分解：根据mid进行分解

  2. 合并：第一个有序段和第二个有序段，比较大小放入一个新的数组中
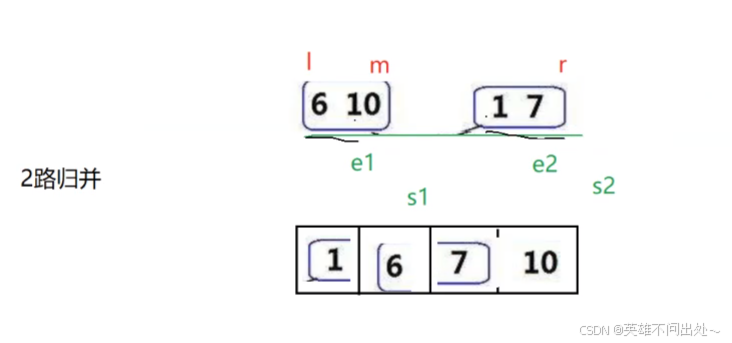
    在这里插入图片描述

// 归并排序public static void mergeSort(int[] array){merge(array,0,array.length - 1);}private static void merge(int[] array,int start,int end){if(start >= end){return;}int mid = (start + end) / 2;// 分解merge(array,start,mid);merge(array,mid + 1,end);// 合并mergeHeB(array,start,mid,end);}private static void mergeHeB(int[] array, int left, int mid, int right) {int s1 = left;int e1 = mid;int s2 = mid + 1;int e2 = right;// 新数组的下标int k = 0;int[] tmpArray = new int[right - left + 1];while(s1 <= e1 && s2 <= e2){if(array[s1] < array[s2]){tmpArray[k++] = array[s1++];}else{tmpArray[k++] = array[s2++];}}while(s1 <= e1){tmpArray[k++] = array[s1++];}while(s2 <= e2){tmpArray[k++] = array[s2++];}// left是因为有左边还有右边的数组// tmpArray是临时数组,会销毁的,需要拷贝回原来的数组for(int i = 0;i < tmpArray.length;i++){array[i + left] = tmpArray[i];}}

分析

  1. 时间复杂度：O(N * logN)
  2. 空间复杂度：O(N)，因为每次合并数组的时候要开O(N)大小的额外空间
  3. 稳定性：稳定的排序

非递归实现归并排序

  1. 先一个一个有序，两个两个有序，四个四个有序，八个八个有序…
  2. gap = 1
    left = i
    mid = left + gap - 1
    right = mid + gap
    gap *= 2
  3. 每组合并完，最终就有序了

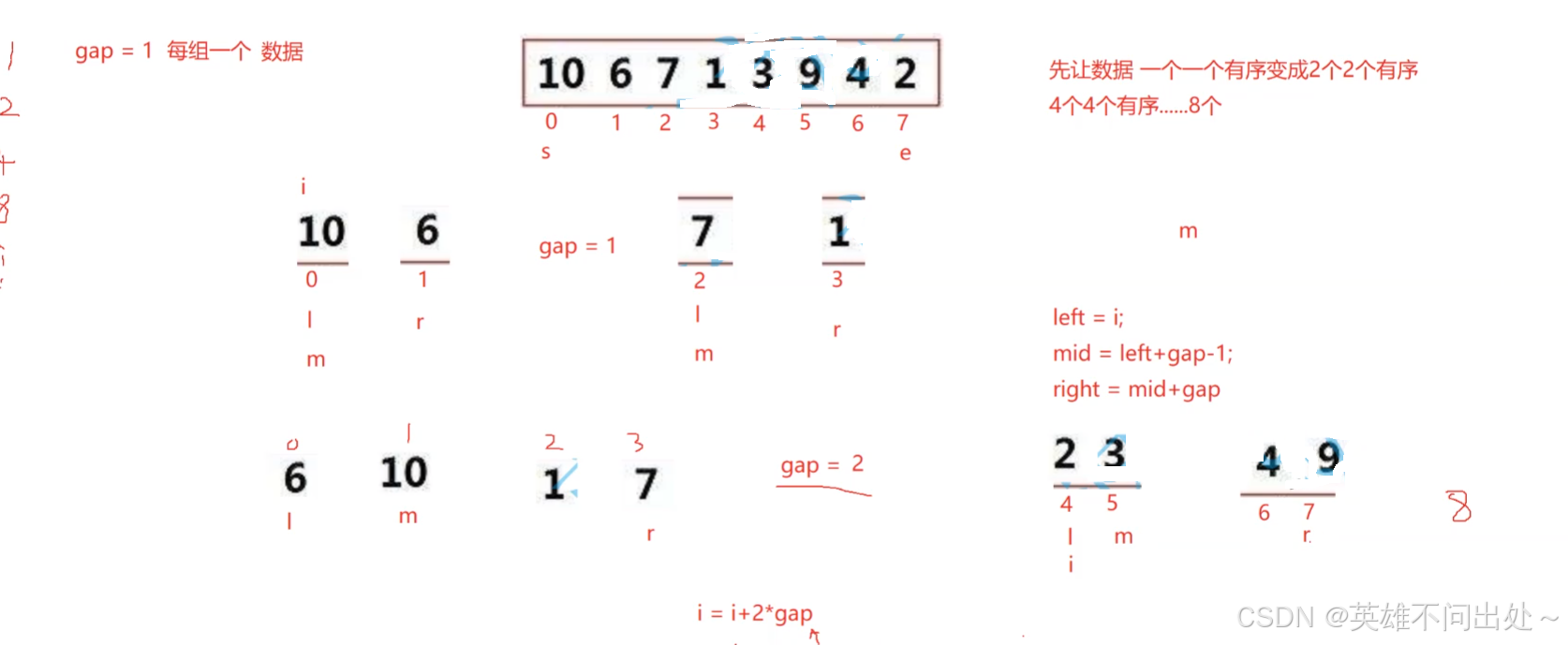
在这里插入图片描述

// 非递归实现归并排序public static void mergeSortNor(int[] array){// gap表示每组的数据个数int gap = 1;while(gap < array.length){for(int i = 0;i < array.length;i = i + 2 * gap){int left = i;// mid和right可能会越界// 比如只有5个元素// 分解右边一半的时候// l = i mid = 5 r = 7int mid = left + gap - 1;int right = mid + gap;if(mid >= array.length){mid = array.length - 1;}if(right >= array.length){right = array.length - 1;}mergeHeB(array,left,mid,right);}gap *= 2;}}

海量数据的排序

  1. 使用归并排序进行外部排序，如果内存中不够空间的话

在这里插入图片描述

非比较的排序

计数排序

  1. 通过统计每次数字出现的次数，最后按照顺序从小到大输出这些数字
  2. 适用的场景：指定范围内的数据

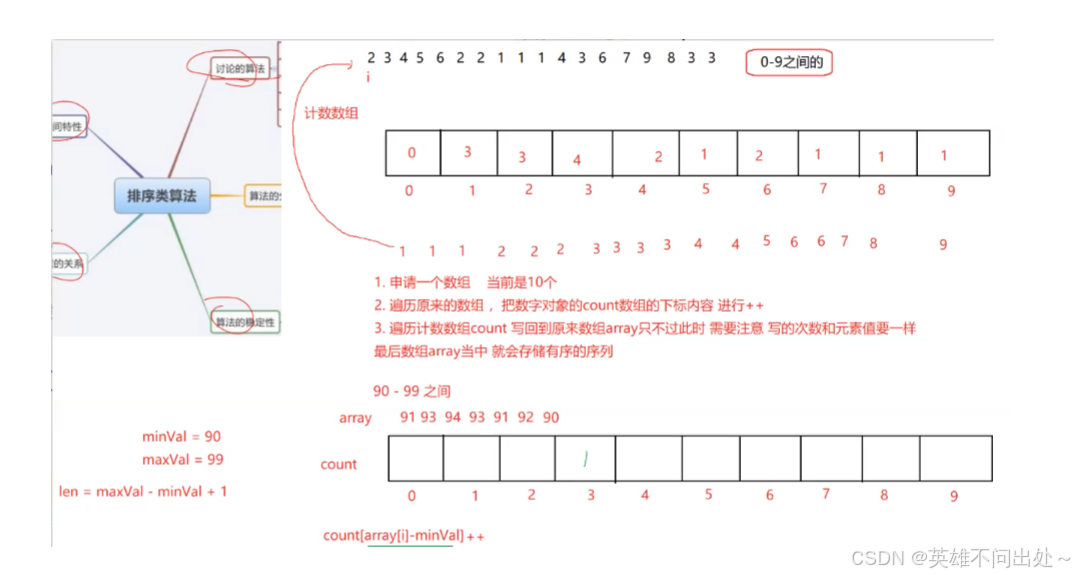
在这里插入图片描述

// 计数排序,指定范围内的数据进行排序
// O(Max(N，范围))public static void countSort(int[] array){int minVal = array[0];int maxVal = array[0];// O(N)for(int i = 0;i < array.length;i++){if(minVal > array[i]){minVal = array[i];}if(maxVal < array[i]){maxVal = array[i];}}int len = maxVal - minVal + 1;int[] count = new int[len];// O(N)for(int i = 0;i < array.length;i++){count[array[i] - minVal]++;}// 写回array数组中// O(范围)// 因为count数组集中于一个数字,那么也是O(范围)// 如果count数组不集中于一个数子,也是N倍的范围// 也是O(范围)int k = 0;for(int i = 0;i < count.length;i++){while(count[i] > 0){array[k++] = i + minVal;count[i]--;}}}

分析

  1. 时间复杂度：O(Max(N，范围))
  2. 空间复杂度：O(范围)
  3. 稳定性：稳定的排序

基数排序

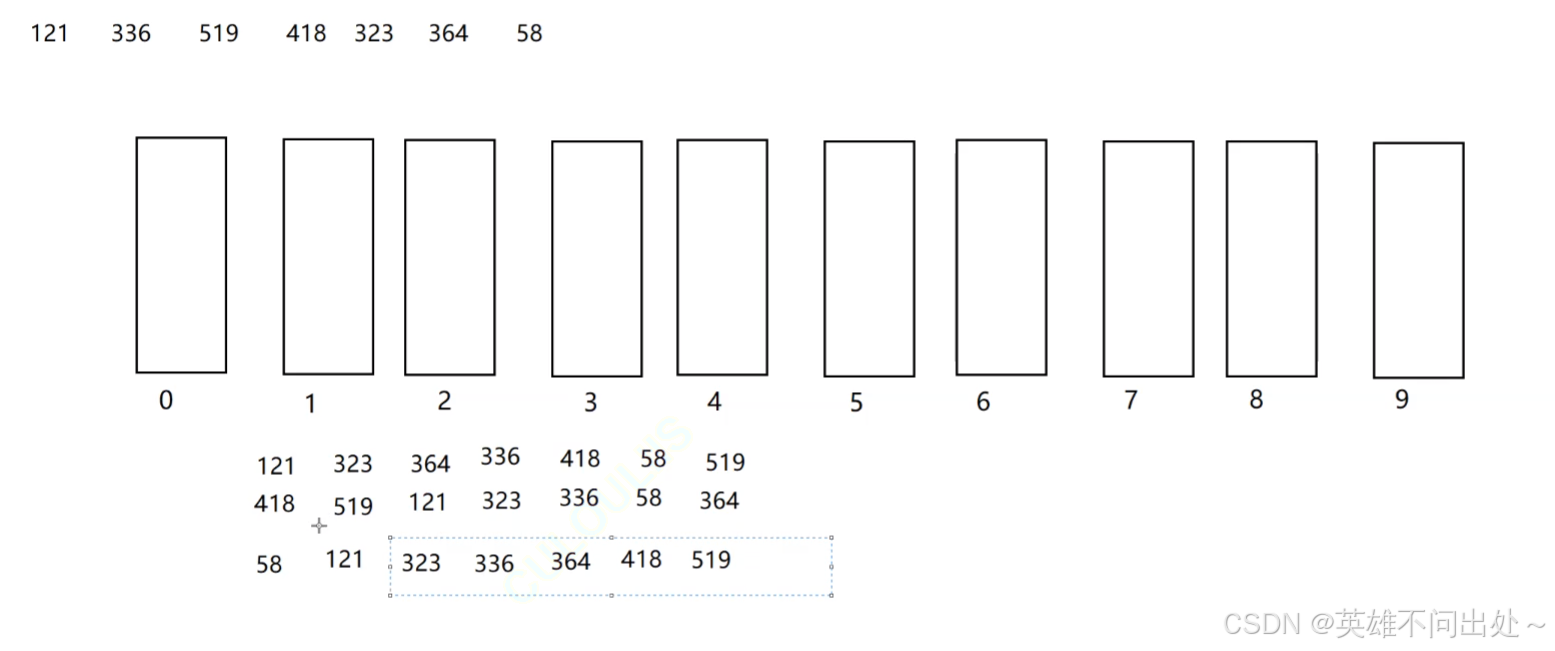
  1. 开10个大小的空间，分别依次比较个位大小，十位大小和百位大小，最终达到有序，每个空间都是一个队列

在这里插入图片描述

桶排序

  1. 先把数字放入一个范围的区间内进行排序，排好序依次拿出来，最终就有序了

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
如若转载，请注明出处：http://www.pswp.cn/pingmian/90924.shtml
繁体地址，请注明出处：http://hk.pswp.cn/pingmian/90924.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

日本IT就职面试|仪容礼仪篇分享建议

日本IT就职面试|仪容礼仪篇分享建议

日系企業で好印象を与える「身だしなみ」と「面接マナー」ガイドこんにちは。 日系企業への就職・転職活動をされている方にとって、「第一印象」は合否を左右する大切なポイントですよね。実は、面接の評価は入室の瞬間から始まっていると言っても過言ではありません。 今回は…
阅读更多...
英语听力口语词汇-8.美食类

英语听力口语词汇-8.美食类

1.crispy,crisp adj.酥脆的&#xff0c;易碎的 2.sweet adj.甜的 比如说chocolate is so sweet and delicious 3.chewy adj.难嚼的&#xff0c;难咽的 4.oatmeal n.燕麦粉 5.pickle n.泡菜 7.stir-fry v.炒菜 8.bacon n.咸肉&#xff0c;熏肉 9.yummy adj.美味可口的 1…
阅读更多...
力扣7:整数反转

力扣7:整数反转

力扣7:整数反转题目思路代码题目 给你一个 32 位的有符号整数 x &#xff0c;返回将 x 中的数字部分反转后的结果。 如果反转后整数超过 32 位的有符号整数的范围 [−2^31, 2^31 − 1] &#xff0c;就返回 0。 思路 这道题我们可以分成两部分来做&#xff0c;一是完成反转二…
阅读更多...
PWM信号控制电机

PWM信号控制电机

1&#xff1a;环境 STM32F103C8T6 KEIL5.38 2个电机 2个轮子 1个L298N STLINKV2 CH340 1个4位独立按键 杜邦线若干 2&#xff1a;代码 key.h #ifndef __KEY_H #define __KEY_H#include "stm32f10x.h"extern volatile uint8_t key_t ; extern volatile uint8_t …
阅读更多...
开源赋能产业，生态共筑未来 | 开源科学计算与系统建模（openSCS）分论坛圆满举行

开源赋能产业，生态共筑未来 | 开源科学计算与系统建模（openSCS）分论坛圆满举行

2025开放原子开源生态大会于7月23日-24日在北京国家会议中心召开。本届大会以“开源赋能产业&#xff0c;生态共筑未来”为主题&#xff0c;汇聚政、产、学、研、用、金、创、投等各领域开源力量&#xff0c;聚焦开源政策导向、生态发展趋势、开源产业实践&#xff0c;共探中国…
阅读更多...
Android广播机制体系初识

Android广播机制体系初识

Android广播机制体系大白话把Android的广播机制想象成小区里的“大喇叭”谁在喊话&#xff1f;任何App或系统都能当“大喇叭”&#xff0c;比如喊一嗓子“电量不足啦&#xff01;”&#xff08;这就是发送广播&#xff09;谁在听&#xff1f;其他App只要“竖起耳朵”&#xff0…
阅读更多...
微信小程序点击输入框时，顶部导航栏被遮挡问题如何解决？

微信小程序点击输入框时，顶部导航栏被遮挡问题如何解决？

前言 不知道大家开发微信小程序的时候有没有遇到这么一个问题&#xff0c;就是在表单页面中&#xff0c;点击输入框后&#xff0c;输入框顶起会把顶部栏给遮挡住&#xff0c;如下图所示&#xff1a;遇到这种情况有没有解决的办法呢&#xff1f;能不能既将页面顶起&#xff0c;同…
阅读更多...
通过具有一致性嵌入的大语言模型（LMMs）实现端到端乳腺癌放射治疗计划制定|文献速递-医学影像算法文献分享

通过具有一致性嵌入的大语言模型（LMMs）实现端到端乳腺癌放射治疗计划制定|文献速递-医学影像算法文献分享

Title题目End-to-end breast cancer radiotherapy planning via LMMs with consistencyembedding通过具有一致性嵌入的大语言模型&#xff08;LMMs&#xff09;实现端到端乳腺癌放射治疗计划制定01文献速递介绍近年来&#xff0c;受大型语言模型&#xff08;LLM&#xff09;启发…
阅读更多...
vscode npm run build打包报ELIFECYCLE

vscode npm run build打包报ELIFECYCLE

npm run build打包报ELIFECYCLE 是内存溢出解决方案&#xff1a;修改build脚本 &#xff1a;"build": "node --max_old_space_size4096 node_modules/vue/cli-service/bin/vue-cli-service.js build",
阅读更多...
【lucene】BlockMaxConjunctionScore

【lucene】BlockMaxConjunctionScore

BlockMaxConjunctionScorer 是 Lucene 8.5 引入的一个高性能交集打分器&#xff08;conjunction scorer&#xff09;&#xff0c;专门用于处理 多条件“与”查询&#xff08;AND 查询&#xff09; 的场景。它基于 Block-Max WAND&#xff08;BMW&#xff09;算法&#xff0c;可…
阅读更多...
Androidstudio 上传当前module 或本地jar包到maven服务器。

Androidstudio 上传当前module 或本地jar包到maven服务器。

1.设置gradle版本到8.0 gradle-wrapper.properties文件中设置&#xff1a; distributionUrlhttps\://mirrors.aliyun.com/macports/distfiles/gradle/gradle-8.0-bin.zip 2.设置项目根目录build.gradle 设置agp版本和maven插件版本&#xff08;和gralde版本有对应关系&#xff…
阅读更多...
Python动态规划：从基础到高阶优化的全面指南

Python动态规划：从基础到高阶优化的全面指南

动态规划&#xff08;Dynamic Programming&#xff09;是解决复杂优化问题的核心技术&#xff0c;也是算法领域的明珠。本文将深入探讨Python实现动态规划的全方位技术&#xff0c;涵盖基础概念、经典问题、优化技巧和实际工程应用&#xff0c;带您掌握这一强大工具的精髓。一、…
阅读更多...
视觉大模型部署实践篇（Docker+dify+ollama安装）

视觉大模型部署实践篇（Docker+dify+ollama安装）

一、概述 目的：实现一个本地化部署的大模型，通过工作流对图像进行一些处理。基于此，我选择了Docker+Dify+Ollama的部署。 具体实现逻辑：Docker来运行dify，dify用来绘制大模型的工作流或者rag等，Ollama用来部署本地大模型，dify调用Ollama部署的大模型进行推理。 二、Dock…
阅读更多...
服务器启动日志等级

服务器启动日志等级

目录 标准日志等级 服务器启动阶段常见日志 日志配置建议 常见服务器/工具的日志等级配置方式 ET框架 Apache/Nginx 等 Web 服务器 Docker 容器 服务器启动过程中的日志等级是帮助开发者和运维人员理解系统状态的重要工具。常见的日志等级及其含义如下&#xff1a; 标准…
阅读更多...
linux_centos7安装jdk8_采用jdk安装包安装

linux_centos7安装jdk8_采用jdk安装包安装

你问我为什么不用yum? 我yum安装不了&#xff0c;我也解决不了qwq. 文章目录一.下载安装包1.找到安装包下载位置2.上传安装包到linux3.解压jdk安装包4.配置环境一.下载安装包 1.找到安装包下载位置 去官网找到你要下载jdk版本&#xff1a; Oracle官网 下面演示安装jdk8的&am…
阅读更多...
Linux驱动23 --- RkMedia 使用

Linux驱动23 --- RkMedia 使用

目录 一、上电自动挂载 二、RkMedia 2.1 认识 RkMedia rtsp rtmp RTSP 和 RTMP 的选择 2.2 安装 VLC 2.2 RkMedia 例程使用 一、上电自动挂载 cd /etc/init.d/ vi Smyprofile.sh 添加这个内容 #!/bin/sh ifconfig eth0 192.168.66.88 mount -t nfs 192.168.66.66…
阅读更多...
Linux:线程同步与线程互斥

Linux:线程同步与线程互斥

线程互斥竞态条件当多个线程&#xff08;或进程&#xff09;并发访问和操作同一个共享资源&#xff08;如变量、文件、数据库记录等&#xff09;时&#xff0c;最终的结果依赖于这些线程执行的相对时序&#xff08;即谁在什么时候执行了哪条指令&#xff09;。 由于操作系统调度…
阅读更多...
HTML 常用标签速查表

HTML 常用标签速查表

HTML 常用标签速查表 &#x1f9f1; 结构类标签 标签含义用途说明<html>HTML文档根元素所有HTML内容的根节点<head>头部信息放置元信息&#xff0c;如标题、引入CSS/JS等<body>页面内容主体所有可视内容的容器&#x1f4dd; 文本与标题标签 标签含义用途说…
阅读更多...
1.gradle安装(mac)

1.gradle安装(mac)

1.下载二进制包 官网下载&#xff1a;Gradle Releases 国内镜像&#xff08;腾讯云&#xff09;&#xff1a;https://mirrors.cloud.tencent.com/gradle/ 2.解压并配置环境变量 解压到指定目录&#xff08;示例&#xff1a;/opt/gradle&#xff09; sudo mkdir -p /opt/gr…
阅读更多...
Rust赋能土木工程数字化

Rust赋能土木工程数字化

基于Rust语言在数字化领域应用 基于Rust语言在土木工程数字 以下是基于Rust语言在土木工程数字化领域的30个实用案例，涵盖结构分析、BIM、GIS、传感器数据处理等方向。案例均采用Rust高性能、安全并发的特性实现，部分结合开源库或算法。 结构分析与计算 有限元分析框架 使…
阅读更多...
最新文章

Copyright @ 2022~2023