文章目录
- 背景
- 设计思路
- 方案
- 结论
- 高斯分布(正态分布)
背景
某电商公司跟某银行有合作,推进银行信用卡办卡&流水,使用此银行信用卡用户,支付可以随机立减10~30元。其实公司每一笔都可获得30元支付立减金,所以,老板希望用户获取的立减金统计平均值约等于15元,这样相当于公司每一笔支付都能赚15元。
设计思路
1)需要随机立减,所以需要一个随机数算法。
2)需要有统计平均数,使得平均立减金额约等于15元
方案
(一)加权随机算法
原理:为不同金额区间分配不同的权重,金额越小权重越高
优势:可以精确控制每个金额的出现概率,容易理解和调整
实现:预定义金额值和对应权重,根据权重随机选择
(二)随机数池
原理:预先生成一个符合要求的随机数集合,使用时从中随机抽取
优势:保证整体分布符合预期,性能较好
实现:按比例生成不同区间的数值,然后打乱顺序存储在池中
(三)高斯分布(正态分布)算法
原理:利用正态分布特性,设置合适的均值和标准差
优势:数学理论基础扎实,分布自然
实现:使用Random.nextGaussian()生成正态分布随机数,映射到目标区间
另外三种方案是通义灵码默认生成的方案。
#file:/Users/liunian/IdeaProjects/study/src/main/java/org/example/random/PayCutAmount.java
package org.example.random;import java.util.*;/*** 支付立减金额计算类* 实现一个随机算法,使立减金额在10-30元之间,平均值约为15元*/
public class PayCutAmount {private static final Random random = new Random();// ==================== 方案1:三角分布数池 ====================/*** 计算支付立减金额 - 三角分布方法* 算法目标:在10-30元范围内生成随机立减金额,长期平均值约为15元** @return 立减金额(单位:元)*/public static double calculateCutAmount() {// 使用三角分布来实现期望值为15的随机数// 三角分布公式:min + (max - min) * (sqrt(r1 * r2))// 其中r1和r2是两个0-1之间的随机数double min = 10.0;double max = 30.0;// 方法1:使用三角分布(推荐)double r1 = random.nextDouble();double r2 = random.nextDouble();double cutAmount = min + (max - min) * Math.sqrt(r1 * r2);// 确保结果在范围内return Math.max(min, Math.min(max, cutAmount));}// ==================== 方案2:简单线性分布 ====================/*** 简单线性分布方法(备选)* 使用平方根方法来偏向较小值** @return 立减金额(单位:元)*/public static double calculateCutAmountSimple() {double min = 10.0;double max = 30.0;// 使用平方根来创建偏向小值的分布double r = Math.sqrt(random.nextDouble());return min + (max - min) * r;}// ==================== 方案3:Beta分布 ====================/*** 基于Beta分布的方法* 通过调整α和β参数来控制分布形状** @return 立减金额(单位:元)*/public static double calculateCutAmountBeta() {double min = 10.0;double max = 30.0;// Beta分布参数,α<1, β>1 使得分布左偏double alpha = 0.8;double beta = 1.5;// 简化的Beta分布采样double x = Math.pow(random.nextDouble(), 1/alpha);double y = Math.pow(random.nextDouble(), 1/beta);double betaValue = x / (x + y);return min + (max - min) * betaValue;}// ==================== 方案4:加权平均算法 ====================/*** 加权平均算法实现* 通过为不同金额区间设置不同的权重来控制平均值* * @return 立减金额(单位:元)*/public static double calculateByWeightedAverage() {// 定义金额区间和对应的权重// 为了使平均值接近15,给较小金额更高权重double[] amounts = {10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30};double[] weights = {11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1}; // 权重递减// 计算总权重double totalWeight = 0;for (double weight : weights) {totalWeight += weight;}// 生成随机数并根据权重选择金额double randomValue = random.nextDouble() * totalWeight;double cumulativeWeight = 0;for (int i = 0; i < amounts.length; i++) {cumulativeWeight += weights[i];if (randomValue <= cumulativeWeight) {return amounts[i];}}// 理论上不会到达这里return amounts[amounts.length - 1];}// ==================== 方案5:随机数池 ====================// 随机数池,预先生成符合要求的数值private static final List<Double> randomPool = generateRandomPool();/*** 生成随机数池* 预先生成一组符合平均值要求的随机数* * @return 随机数池*/private static List<Double> generateRandomPool() {List<Double> pool = new ArrayList<>();Random rand = new Random();// 生成200个随机数,其中大部分是较小值,少量是较大值// 保证整体平均值约为15for (int i = 0; i < 120; i++) {// 生成10-17之间的数(占比60%)double value = 10 + rand.nextDouble() * 7;pool.add(Math.round(value * 100.0) / 100.0); // 保留两位小数}for (int i = 0; i < 60; i++) {// 生成17-24之间的数(占比30%)double value = 17 + rand.nextDouble() * 7;pool.add(Math.round(value * 100.0) / 100.0);}for (int i = 0; i < 20; i++) {// 生成24-30之间的数(占比10%)double value = 24 + rand.nextDouble() * 6;pool.add(Math.round(value * 100.0) / 100.0);}// 打乱顺序Collections.shuffle(pool, rand);return pool;}/*** 从随机数池中获取随机立减金额* * @return 立减金额(单位:元)*/public static double calculateFromRandomPool() {int index = random.nextInt(randomPool.size());return randomPool.get(index);}// ==================== 方案6:高斯正态分布 ====================/*** 高斯正态分布算法实现* 使用正态分布生成随机数,然后映射到目标区间* * @return 立减金额(单位:元)*/public static double calculateByGaussian() {// 设置期望值和标准差// 为了让平均值接近15,我们设置期望值略小于15double mean = 14.5; // 期望值double stdDev = 4.0; // 标准差// 生成正态分布的随机数double gaussianValue = random.nextGaussian() * stdDev + mean;// 将结果限制在10-30范围内gaussianValue = Math.max(10, Math.min(30, gaussianValue));// 保留两位小数return Math.round(gaussianValue * 100.0) / 100.0;}/*** 测试方法:验证所有算法的平均值是否接近15元*/public static void main(String[] args) {int testCount = 100000;double sum1 = 0, sum2 = 0, sum3 = 0, sum4 = 0, sum5 = 0, sum6 = 0;System.out.println("测试" + testCount + "次随机立减金额算法:");System.out.println("================================");// 测试三角分布方法for (int i = 0; i < testCount; i++) {double amount = calculateCutAmount();sum1 += amount;}double average1 = sum1 / testCount;System.out.println("三角分布方法:");System.out.println(" 平均立减金额: " + String.format("%.2f", average1) + "元");System.out.println(" 与目标值15元的偏差: " + String.format("%.4f", Math.abs(15 - average1)) + "元");// 测试简单线性分布方法for (int i = 0; i < testCount; i++) {double amount = calculateCutAmountSimple();sum2 += amount;}double average2 = sum2 / testCount;System.out.println("简单线性分布方法:");System.out.println(" 平均立减金额: " + String.format("%.2f", average2) + "元");System.out.println(" 与目标值15元的偏差: " + String.format("%.4f", Math.abs(15 - average2)) + "元");// 测试Beta分布方法for (int i = 0; i < testCount; i++) {double amount = calculateCutAmountBeta();sum3 += amount;}double average3 = sum3 / testCount;System.out.println("Beta分布方法:");System.out.println(" 平均立减金额: " + String.format("%.2f", average3) + "元");System.out.println(" 与目标值15元的偏差: " + String.format("%.4f", Math.abs(15 - average3)) + "元");// 测试加权平均算法for (int i = 0; i < testCount; i++) {double amount = calculateByWeightedAverage();sum4 += amount;}double average4 = sum4 / testCount;System.out.println("加权平均算法:");System.out.println(" 平均立减金额: " + String.format("%.2f", average4) + "元");System.out.println(" 与目标值15元的偏差: " + String.format("%.4f", Math.abs(15 - average4)) + "元");// 测试随机数池方法for (int i = 0; i < testCount; i++) {double amount = calculateFromRandomPool();sum5 += amount;}double average5 = sum5 / testCount;System.out.println("随机数池方法:");System.out.println(" 平均立减金额: " + String.format("%.2f", average5) + "元");System.out.println(" 与目标值15元的偏差: " + String.format("%.4f", Math.abs(15 - average5)) + "元");// 测试高斯正态分布方法for (int i = 0; i < testCount; i++) {double amount = calculateByGaussian();sum6 += amount;}double average6 = sum6 / testCount;System.out.println("高斯正态分布方法:");System.out.println(" 平均立减金额: " + String.format("%.2f", average6) + "元");System.out.println(" 与目标值15元的偏差: " + String.format("%.4f", Math.abs(15 - average6)) + "元");}
}运行结果
测试100000次随机立减金额算法:
================================
三角分布方法:平均立减金额: 18.86元与目标值15元的偏差: 3.8631元
简单线性分布方法:平均立减金额: 23.32元与目标值15元的偏差: 8.3199元
Beta分布方法:平均立减金额: 18.12元与目标值15元的偏差: 3.1212元
加权平均算法:平均立减金额: 16.65元与目标值15元的偏差: 1.6520元
随机数池方法:平均立减金额: 17.21元与目标值15元的偏差: 2.2119元
高斯正态分布方法:平均立减金额: 14.77元与目标值15元的偏差: 0.2299元
结论
可以看出,高斯正态分布的结果是最接近15元的,线性、三角分布、beta分布的结果与15元都相差不小,如果不想通过记录统计每一个立减的值来算出平均值,高斯分布是最合适的算法。
高斯分布(正态分布)
正态分布(Normal distribution),又称为常态分布或高斯分布,通常记作X~N(μ ,σ2)。其中, μ是正态分布的数学期望(均值), σ2是正态分布的方差。μ = 0,σ = 1的正态分布被称为标准正态分布 。
正态分布的概率密度函数显示为典型的钟形曲线,这一形状类似于寺庙中的大钟,因此也常被称为钟形曲线。作为一种连续分布,正态分布拥有完备的概率密度函数、累积分布函数、矩生成函数和特征函数等表达形式,并且具备明确的期望(即均值)、方差、偏度和峰度等数值特征。中心极限定理阐述了在一定条件下,多个独立同分布的随机变量的平均值会趋向于正态分布,这一现象在样本量增大时尤为显著。
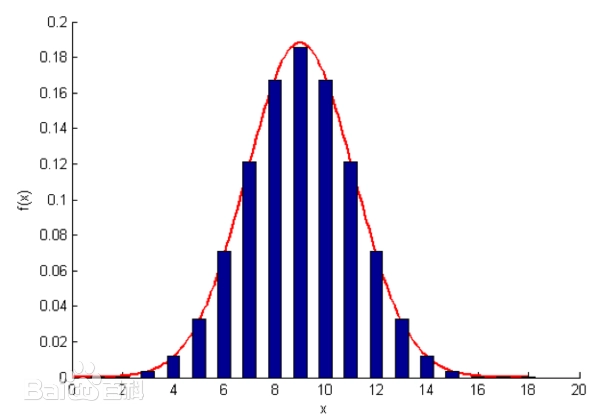


)
韦东山老师学习笔记(课程听不懂的话试着来看看我的学习笔记吧))
)

)





)




)

