深度学习：激活函数Activaton Function

一、为什么需要激活函数？

神经网络本质上是多个线性变换（矩阵乘法）叠加。如果没有激活函数，即使叠加多层，整体仍等价于一个线性函数：

$f(x) = W_nW_{n-1}\cdot \cdot \cdot W_1x+b$

这样的网络无法学习和拟合现实世界中复杂的非线性关系。

激活函数的作用：

在每一层加入非线性变换，使得网络具有逼近任意非线性函数的能力。
激活神经元，产生“信息通过/抑制”的门控效果。

二、常见激活函数列表与直觉图示

名称

公式

输出范围

图像形状

是否中心对称

使用场景

Sigmoid

$\sigma \left ( x \right )=\frac{1}{1+e^{-x}}$

（0，1）

S型

否

概率输出，二分类

Tanh

$tanh(x)=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}$

（-1，1）

中心对称S型

是

RNN隐藏层

ReLU

$f(x) = max(0,x)$

[0，+∞）

截断线性

否

默认隐藏层函数

Leaky ReLU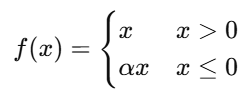

(-∞，+∞)

左侧带缓坡

否

缓解ReLU死神经元问题

ELU/GELU

Smooth ReLU变体

（-1，∞）

平滑曲线

否

深层网络（如BERT）

Softmax

$Softmax(x_{i})=\frac{e^{x_{i}}}{\sum_{j}^{e^{x_{j}}}}$

（0，1）且总和=1

多维映射

否

多分类输出层

三、每种激活函数详细讲解

3.1 Sigmoid函数（逻辑激活）

$\sigma (x) = \frac{1}{1+e^{-x}}$

特性：

输出范围在(0，1)，可理解为概率
单调递增，饱和区梯度小（梯度消失问题严重）
在0附近比较线性，但远离0时趋近于平稳

优点：

直观表示“激活程度”（介于0与1之间）
在早期神经网络和输出层应用广泛

缺点：

梯度消失问题：远离0时梯度趋近于0
输出非中心对称：导致后一层神经元输入偏向正方向

使用建议：

不推荐用于隐藏层
可用于输出为“概率”的任务（如二分类输出层）

3.2 Tanh函数（双曲正切）

$tanh(x) = \frac{e^x-e^{-x}}{e^x+e^{-x}} = 2\sigma (2x)-1$

特性：

输出范围（-1，1），是中心对称的S型函数
在0附近几乎线性，表现比Sogmoid更好。

优点：

零均值输出，收敛速度通常比Sigmoid快。

缺点：

也存在梯度消失问题（在±2左右开始饱和）

使用建议：

在RNN等早期模型中较为常见。
若模型对“负激活”有需求，可以使用Tanh。

3.3 ReLU（Rectified Linear Unit）

$f(x)=max(0,x)$

特性：

最常用的激活函数，非线性强，计算简单。
在x＞0区域内导数为1，在x≤0区域内导数为0。

优点：

计算快，易于优化，不易发生梯度消失。
会产生稀疏激活（部分神经元输出为0），提高泛化能力。

缺点：

死亡神经元问题：一旦某个神经元进入负区间并梯度为0，则该神经元永远不会激活。

使用建议：

深度神经网络的隐藏层默认激活函数。
若出现大量“死神经元”，可以使用Leaky ReLU或ELU替代。

3.4 Leaky ReLU

$f(x) = x(x\geq 0),\alpha x(x<0)$ α通常为0.01

特性：

为ReLU的改进版本，在负区间保留少量梯度。

优点：

缓解了ReLU的“死亡神经元”问题。
在某些任务上收敛更稳定。

缺点：

依赖于α超参数，需调参。

使用建议：

如果ReLU网络中出现大量神经元输出恒为0，可尝试替换为Leaky ReLU

3.5 GELU（Gaussian Error Linear Unit）

$f(x) = x \cdot \phi (x)$ ， $\phi (x)$ 是标准正态分布的累积分布函数

特性：

是ReLU与Sigmoid的混合形式。
表现为平滑的非线性函数。

优点：

在Transformer，BERT，ViT中广泛使用。
理论上更优，经验上在大模型中性能更好。

使用建议：

在使用Transformer，BERT，T5等模型，默认激活就是GELU。

3.6 Softmax（用于输出层）

$Softmax(x_i)=\frac{e^{x_i}}{\sum_{j}^{}e^{x_j}}$

特性：

将向量转换为“概率分布”：每个值在(0,1)，总和为1。
常用于多分类任务的输出层。

使用建议：

不用于隐藏层，仅用于输出层。
通常与交叉熵损失函数一起使用。

四、总结对比表

函数	是否线性	输出范围	是否对称	梯度问题	使用推荐
Sigmoid	否	(0, 1)	否	易梯度消失	输出层（二分类）
Tanh	否	(-1, 1)	是	易梯度消失	RNN、需要对称时
ReLU	否	[0, ∞)	否	死神经元	默认隐藏层
Leaky ReLU	否	(-∞, ∞)	否	有梯度	替代 ReLU
GELU	否	(-∞, ∞)	否	平滑收敛好	BERT等大模型
Softmax	否	(0, 1) 且和为1	否	N/A	多分类输出

五、激活函数的三大核心指标

指标	含义	重要性
非线性能力	是否能打破线性叠加	所有激活函数的基本功能
是否有梯度	梯度在输入范围内是否为0	决定反向传播是否可行
零中心性	输出是否以0为中心	有助于加速收敛，避免梯度偏移

六、隐藏层和输出层的激活函数选择原则

层类型	推荐激活函数	原因
隐藏层	ReLU/Leaky ReLU/GELU	快速收敛，低计算开销，有效抑制梯度问题
输出层-二分类	Sigmoid	输出概率，可与BCE Loss配合
输出层-多分类	Softmax	输出概率分布，可与CrossEntropyLoss配合
输出层-回归	无激活/Linear	输出连续值（如房价）

七、ReLU系列变体的扩展图谱

1.Leaky ReLU：缓解死神经元问题

2.PReLU（Parametric ReLU）:负斜率α可学习

3.RReLU（Randomized ReLU）:训练时负斜率为随机数

4.ELU（Exponential Linear Unit）:负区间指数形状，避免输出偏正

5.SELU（Scaled ELU）:自归一化网络（Self-Normalizing NN）

八、实际工程中激活函数的选型建议

场景	推荐函数	理由
默认情况	ReLU	简单快速，表现好
出现大量死神经元	Leaky ReLU/PReLU	保持梯度
大模型（Transformer等）	GELU	平滑非线性，更强表征能力
医疗/金融等数据对称	Tanh	输出中心对称，利于稳定性
多标签任务输出层	Sigmoid	与BCE loss搭配使用
多分类任务输出层	Softmax	与交叉熵搭配使用

九、激活函数与神经网络结构的关系

激活函数不是孤立使用的，而是与网络层数，归一化方法，损失函数等协同设计：

网络结构	建议激活函数	原因
MLP(多层感知机)	ReLU/LeakyReLU	层数少，避免梯度消失即可
CNN（卷积网络）	ReLU/LeakyReLU	图像任务中默认激活，训练快
RNN/LSTM	Tanh/Sigmoid（门控）	RNN天然处理时序信息，Tanh为主，Sigmoid用于控制门结构
Transformer	GELU/ReLU	BERT,GPT中使用GELU收敛更平稳，ReLU计算更快
自归一化网络（SNN）	SELU	与特殊初始化+dropout配合，自动归一化每层输出
GAN生成器	ReLU/LeakyReLU	生成端需非线性表达能力强
GAN判别器	LeakyReLU	判别器中避免ReLU死神经元影响判别能力

十、训练中因激活函数导致的典型问题与解决方案

问题	可能原因	解决方案
训练不收敛	Sigmoid/Tanh导致梯度消失	改用ReLU/GELU
大量神经元恒为0	ReLU死神经元问题	改用LeakyReLU/PReLU
loss起伏大	梯度爆炸 or 梯度不稳定	尝试使用平滑激活函数（GELU/Swish）
模型准确率震荡	输出分布不均衡	检查是否中心兑成（可尝试Tanh/SELU）

十一、激活函数与归一化层的顺序问题

在使用BatchNorm/LayerNorm时，激活函数的位置非常关键。

顺序类型	建议顺序	说明
CNN(BatchNorm)	Conv➡BN➡ReLU	主流做法，BN规范分布后再非线性激活
Transformer(LayerNorm)	LN➡Linear➡GELU	大模型默认顺序（PreNorm）
ResNet残差结构	ReLU放在跳跃前还是后？	大多在残差和主路路径相见之后ReLU

十二、激活函数的梯度可视化

激活函数	导数（梯度）	梯度图像直觉
Sigmoid	σ′(x)=σ(x)(1−σ(x))\sigma'(x) = \sigma(x)(1 - \sigma(x))	梯度最大在 x=0，越远越趋近于0（易梯度消失）
Tanh	tanh⁡′(x)=1−tanh⁡2(x)\tanh'(x) = 1 - \tanh^2(x)	梯度范围比 Sigmoid 更广，但仍有饱和问题
ReLU	f′(x)=1 if x>0;0 elsef'(x) = 1 \text{ if } x>0; 0 \text{ else}	梯度恒定，简单高效
Leaky ReLU	f′(x)=1 if x>0;α elsef'(x) = 1 \text{ if } x>0; \alpha \text{ else}	保留负区间小梯度
GELU	近似导数为高斯变换	平滑过渡，梯度分布均衡（大模型表现好）

十三、激活函数的数学本质：非线性特征空间映射

从数学角度来看，激活函数在整个神经网络中充当非线性特征映射角色：

网络每一层执行的是

$x_{l+1} = \phi (W_lx_l+b_l)$

其中 $\phi$ 是激活函数

本质上是将低维空间的线性表示映射到高维非线性空间，从而可以更好地学习复杂关系（类似SVM的核函数思想）

十四、小结

场景	首选激活函数	替代备选
图像分类	ReLU	Leaky ReLU / GELU
序列建模	Tanh / GELU	ReLU
大型Transformer	GELU	Swish
输出为概率（二分类）	Sigmoid	无
多分类输出层	Softmax	无
GAN 判别器	Leaky ReLU	ReLU
出现死神经元	Leaky ReLU	PReLU