电子装备试验方案优选是一个典型的多属性决策问题，通常涉及指标复杂、信息不完整、数据量少且存在不确定性的特点。灰色系统理论（Grey System Theory）特别擅长处理“小样本、贫信息”的不确定性问题，因此非常适合用于此类方案的优选。灰色关联分析（Grey Relational Analysis, GRA） 是其中的核心方法。

以下详细阐述基于灰色关联分析的电子装备试验方案优选模型及算法：

一、 问题定义

目标： 从多个备选电子装备试验方案 {S1, S2, …, Sm} 中，选择综合性能最优（或最满意）的方案。

评价指标： 建立一套科学、全面的评价指标体系 {C1, C2, …, Cn}。这些指标应涵盖试验的核心目标，例如：

技术性能指标： 试验覆盖性、测试精度、测试效率、故障注入能力、逼真度等。

经济性指标： 试验成本（设备、人力、消耗品）、试验周期。

风险性指标： 技术实现难度、进度风险、安全风险、数据可靠性风险。

保障性指标： 场地要求、设备复用率、人员技能要求、后勤支持难度。

适用性指标： 方案灵活性、扩展性、对不同装备型号的适应性。

数据特点： 指标值可能来源于专家打分（定性指标）、历史数据、仿真数据或部分实测数据。数据量通常有限，且部分信息可能模糊不清（灰色性）。

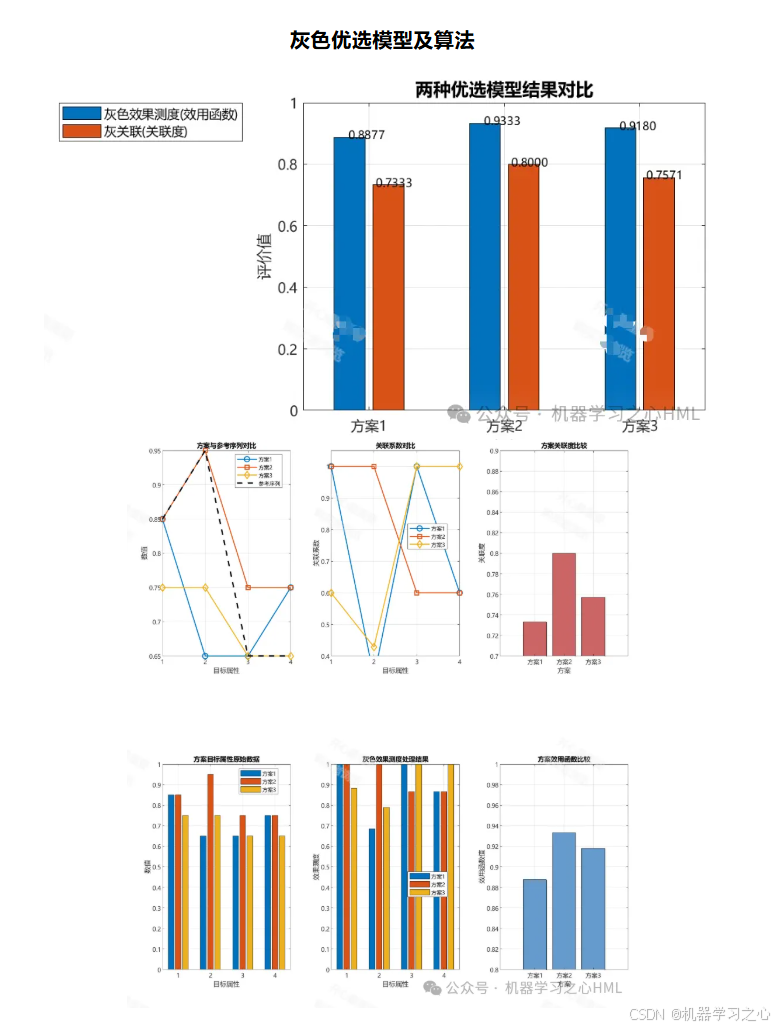
二、 灰色优选模型：基于灰色关联分析（GRA）

核心思想：通过计算各备选方案与一个虚构的“最优参考方案”（或“最劣参考方案”）的关联程度（关联度），来衡量方案的优劣。关联度越大，说明该方案与最优方案的接近程度越高，方案越优。

三、 模型特点与优势

处理“贫信息”能力强： 对数据量要求低，不需要严格的概率分布或大量样本，特别适合电子装备试验这种试验次数有限、数据获取成本高的场景。

能融合定性与定量指标： 通过规范化（如专家打分归一化）可以将定性指标转换为可计算的数值，实现不同类型指标的综合评价。

计算过程相对简单清晰： 算法步骤明确，易于编程实现。

结果直观： 关联度 Γi 提供了方案优劣的直接数值比较。

考虑指标间关联性（间接）： 虽然GRA本身主要处理序列间的几何形状相似性，但通过综合关联度计算，实际上包含了各指标对整体目标的不同贡献（由权重体现）。