一、基础知识
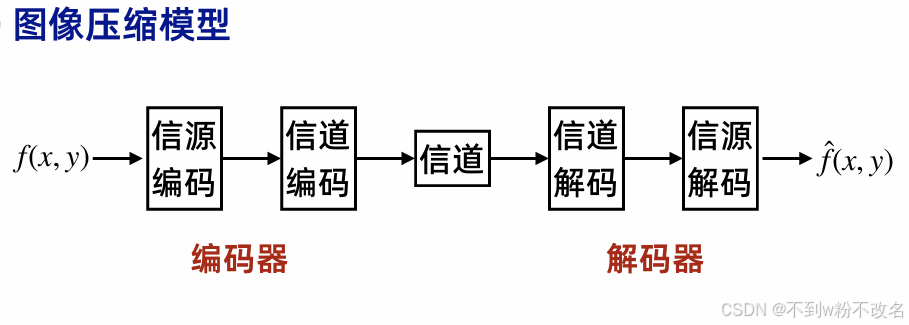
信源编码器:减少或消除输入图像中的编码冗余、像素 间冗余以及心理视觉冗余。
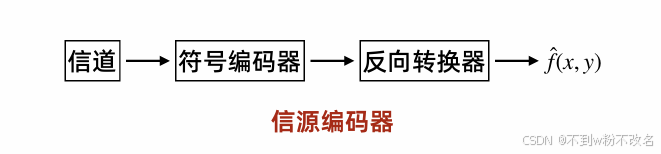
数据的冗余
一、空间冗余(Spatial Redundancy)
1. 定义
图像中相邻像素间的强相关性导致的冗余 —— 同一区域内相邻像素的像素值(如灰度、色彩)往往相似或相同,重复信息未被压缩时会占用额外存储空间。
2. 产生原因
- 自然图像中存在大量平滑区域(如蓝天、墙壁),相邻像素值几乎一致;
- 物体边缘的像素值虽有突变,但边缘两侧的区域内仍存在像素相关性。
3. 压缩应用
- 预测编码(Prediction Coding):利用相邻像素预测当前像素值,仅存储预测误差(如 JPEG 中的 DPCM 预测)。例如,若当前像素值为 100,相邻像素预测值为 98,则仅存储差值 “2”。
- 像素差值编码:计算相邻像素的差值(如相邻行 / 列的差),差值中零值或小值占比高,可通过行程编码(RLE)压缩连续相同差值。
二、编码冗余(Coding Redundancy)
1. 定义
图像中像素值的概率分布与编码方式不匹配导致的冗余 —— 当像素值出现概率不均时,使用等长编码(如 8 位固定编码)会浪费编码空间(即实际编码长度大于信息熵理论最小值)。
2. 数学原理
- 信息熵公式:
,其中p(i)为像素值i出现的概率。
- 若图像中某像素值出现概率p(i)很高(如背景色),其理论编码长度应更短;但等长编码强制所有值占用相同长度(如 8 位),导致总编码长度L>H,差值L−H即为编码冗余。
3. 压缩应用
- 变长编码(Variable - Length Coding):为高频出现的像素值分配短编码,低频值分配长编码。例如:
- 霍夫曼编码(Huffman Coding):根据像素值概率构建编码表,概率越高编码越短;
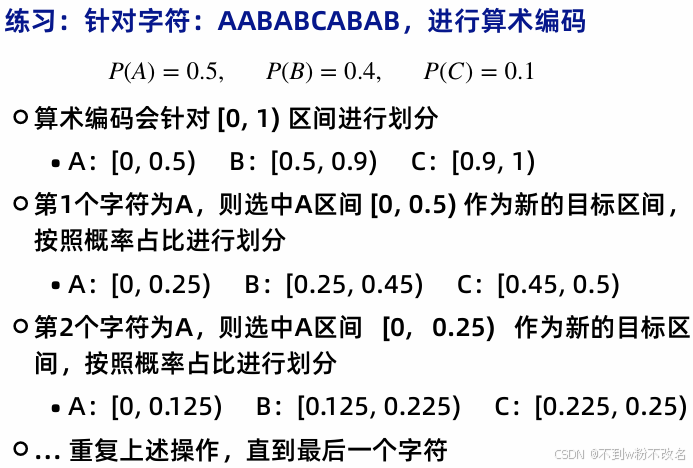
- 算术编码(Arithmetic Coding):将整个像素序列映射为 [0,1) 区间的一个小数,用更少位数表示。
- JPEG 压缩中,对量化后的 DCT 系数进行霍夫曼编码,减少编码冗余。
三、视觉冗余(Visual Redundancy)
1. 定义
基于人类视觉系统(HVS)的感知局限性产生的冗余 —— 图像中部分信息(如高频细节、微小色差)超出人眼分辨能力,即使丢失也不影响主观视觉效果。
2. 生理基础
- 人眼对亮度变化比色彩变化更敏感(如 YUV 色彩空间中 Y 分量优先保留);
- 对图像的高频细节(如细微纹理、快速变化的边缘)分辨力低,对低频轮廓更敏感。
3. 压缩应用
- 量化(Quantization):对图像变换域(如 DCT、小波变换)的高频系数进行粗量化(甚至置零),丢弃人眼不敏感的信息。例如:
- JPEG 中使用 DCT 将图像转换到频率域,对高频系数(对应细节)采用大步长量化,大幅减少数据量;
- JPEG 2000 利用小波变换,对不同频率子带采用不同量化精度,优先保留低频信息。
- 色彩空间转换:将 RGB 转换为 YUV 后,对 UV 分量(色彩)进行降采样(如 4:2:0 采样),利用人眼对色彩分辨率低的特性减少数据量。
四、三种冗余的对比与应用场景
| 冗余类型 | 核心本质 | 典型压缩技术 | 应用场景(举例) |
|---|---|---|---|
| 空间冗余 | 像素间空间相关性 | 预测编码、差值编码、RLE | 无损压缩(如 PNG)、视频帧内压缩 |
| 编码冗余 | 概率分布与编码不匹配 | 霍夫曼编码、算术编码 | 各类压缩的熵编码阶段(如 JPEG) |
| 视觉冗余 | 人眼感知能力局限性 | 量化、频率域滤波、色彩降采样 | 有损压缩(如 JPEG、WebP) |
总结
图像压缩的核心是通过分析不同类型的数据冗余,结合算法针对性优化:
- 空间冗余利用像素相关性减少重复存储;
- 编码冗余通过变长编码匹配概率分布,逼近信息熵下限;
- 视觉冗余则借助人眼特性 “合理丢弃” 无效信息,在压缩效率与视觉质量间平衡。
三种冗余常协同作用(如 JPEG 同时利用空间冗余的 DPCM 预测、编码冗余的霍夫曼编码、视觉冗余的 DCT 量化),实现高效压缩。
图像压缩评价标准
一、冗余度(Redundancy)
1. 定义
指图像数据中可被消除的冗余信息比例,反映压缩算法对数据冗余的利用效率。冗余度越低,说明压缩后数据中无效信息越少。
2. 数学表达与计算
- 信息熵(Entropy, H):表示图像中信息的理论最小编码长度,公式为:
其中 p(i) 为像素值 i 出现的概率,n 为像素值种类数。- 平均编码长度(L):压缩后每个像素的平均编码位数。
- 冗余度公式:
当 L=H 时,冗余度为 0,此时编码达到理论最优(无冗余);若 L>H,冗余度越大,说明编码效率越低。
3. 应用场景
- 用于评估无损压缩算法的效率(如霍夫曼编码、算术编码),衡量其对编码冗余的消除能力。
- 例如:某图像信息熵 H=5 bit / 像素,压缩后平均编码长度 L=6 bit / 像素,则冗余度为 1−5/6≈16.7%,表示存在 16.7% 的编码冗余可进一步优化。
二、编码效率(Coding Efficiency)
1. 定义
衡量压缩算法的编码结果与理论最优编码(信息熵)的接近程度,反映编码过程中对信息的利用效率。
2. 数学表达与计算
- 编码效率公式:
其中 H 为信息熵,L 为平均编码长度。编码效率越高,说明编码结果越接近理论最小值。- 理想情况下,编码效率为 100%(L=H),但实际中因算法复杂度等限制,效率通常小于 100%。
3. 应用场景
- 对比不同编码方式的有效性:
- 霍夫曼编码的编码效率通常在 80%~95%,而算术编码可更接近 100%(因无需将每个符号独立编码,而是处理整个符号序列)。
- 例如:JPEG 压缩中,对量化后的 DCT 系数进行霍夫曼编码,若信息熵 H=3 bit / 系数,平均编码长度 L=3.2 bit / 系数,则编码效率为 3/3.2≈93.75%。
三、保真度(Fidelity)
1. 定义
衡量压缩后图像与原始图像的相似程度,反映压缩算法对图像信息的保留能力,分为无损保真度和有损保真度。
2. 分类及计算方法
(1)无损保真度(适用于无损压缩)
- 压缩前后图像完全一致,保真度为 100%,常用指标:
- 压缩比(Compression Ratio):原始数据量与压缩后数据量的比值,公式为:

例如:原始图像大小为 10MB,压缩后为 2MB,压缩比为 5:1。
- 压缩比(Compression Ratio):原始数据量与压缩后数据量的比值,公式为:
(2)有损保真度(适用于有损压缩)
- 衡量图像质量损失,常用客观指标:
- 均方误差(MSE, Mean Squared Error):计算原始图像 f(i,j) 与压缩图像 f^(i,j) 像素值差的平方均值:
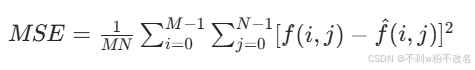
- 峰值信噪比(PSNR, Peak Signal-to-Noise Ratio):基于 MSE 的对数转换,单位为分贝(dB),公式为:
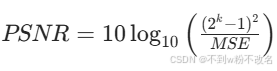
其中 k 为像素值位数(如 8 位灰度图中 k=8,最大值为 255)。PSNR 越高,图像质量越好(通常 30dB 以上视为可接受)。
- 均方误差(MSE, Mean Squared Error):计算原始图像 f(i,j) 与压缩图像 f^(i,j) 像素值差的平方均值:
- 主观指标:
- 主观评分(如 MOS, Mean Opinion Score):通过人类观察者对图像质量打分(1~5 分),更贴合实际感知,但具有主观性。
3. 应用场景
- 有损压缩算法(如 JPEG、WebP)中,用于平衡压缩比与图像质量:
- 调整量化参数可改变保真度:量化步长越大,PSNR 越低,压缩比越高(如 JPEG 的 “质量因子” 从 100 降至 10 时,PSNR 从 40dB 降至 25dB,压缩比从 1:1 升至 20:1)。
四、指标对比与实际应用
| 指标 | 核心作用 | 数值特性 | 典型应用场景 |
|---|---|---|---|
| 冗余度 | 衡量数据冗余消除程度 | 越接近 0 越好 | 无损压缩算法评估 |
| 编码效率 | 衡量编码与理论最优的差距 | 越接近 100% 越好 | 比较不同编码方式的优劣 |
| 保真度 | 衡量图像质量保留能力 | 无损压缩中为 100%,有损压缩中 PSNR 越高越好 | JPEG、视频压缩等有损场景的质量评估 |
总结
- 冗余度与编码效率:从信息论角度评估压缩算法对数据冗余的处理能力,适用于无损压缩场景,两者呈互补关系(冗余度 = 1 - 编码效率)。
- 保真度:聚焦图像质量,是有损压缩的核心指标,需与压缩比结合权衡(如牺牲部分保真度换取更高压缩比)。
实际应用中,需根据需求(如医学图像要求高保真度,网页图片侧重压缩比)选择合适的指标组合评估压缩算法性能。

二、基本压缩方法
根据解压重建后的图像和原始图像之间是否具有误差,图像编码压缩分为两大类
无误差(无失真、无损、信息保持)编码
有误差(有失真或有损)编码
根据编码作用域划分,图像编码为
空间域编码
变换域编码

一、有损压缩(Lossy Compression)
1. 定义与核心原理
- 定义:通过舍弃部分次要信息(如人眼 / 人耳不敏感的高频细节)来减少数据量,压缩过程不可逆,解压后无法完全还原原始数据。
- 核心原理:利用人类感知系统的局限性(如视觉对色彩精度、听觉对高频声音的不敏感),通过量化(Quantization) 等操作丢弃冗余信息,换取高压缩比。
2. 关键技术与算法
(1)变换编码(Transform Coding)
- 流程:
- 将原始数据从空间域 / 时域转换到频率域(如傅里叶变换、DCT 离散余弦变换)。
- 对高频系数进行粗量化(舍弃或近似),保留低频重要信息。
- 对量化后的数据进行熵编码(如霍夫曼编码)。
- 典型算法:
- JPEG(图像):对图像分块进行 DCT 变换,量化高频系数,压缩比可达 10:1~100:1,但会产生 “块效应”(如质量因子过低时边缘模糊)。
- MP3(音频):利用人耳 “掩蔽效应”(高频声音会掩盖低频细节),丢弃感知不到的频率成分,压缩比约 10:1~12:1。
(2)矢量量化(Vector Quantization, VQ)
- 将数据分组为向量,用码本中的近似向量替代原始向量,适用于图像像素块压缩(如早期图像压缩标准),但计算复杂度高。
3. 应用场景
- 多媒体内容:图片(JPEG、WebP)、音频(MP3、AAC)、视频(H.264、H.265)。
- 对细节要求不高的场景:网页图片、流媒体视频、手机拍摄的照片(如手机相机默认启用有损压缩)。
4. 优缺点
- 优点:压缩比高(可达数十至数百倍),适合存储和传输大量多媒体数据。
- 缺点:信息永久丢失,压缩比过高时质量明显下降(如图片模糊、视频色块)。
二、无损压缩(Lossless Compression)
1. 定义与核心原理
- 定义:仅消除数据中的冗余信息(如重复字节、统计冗余),压缩过程可逆,解压后可完全还原原始数据。
- 核心原理:利用数据的统计特性或结构冗余,通过编码算法重新组织数据,减少存储空间,不丢失任何信息。
2. 关键技术与算法
(1)熵编码(Entropy Coding)
- 基于信息熵理论,对出现概率高的符号分配短编码,概率低的符号分配长编码。
- 典型算法:
- 哈夫曼编码(Huffman Coding):根据符号出现频率构建二叉树,生成变长编码,如文本压缩(.txt 文件)。

- 算术编码(Arithmetic Coding):将整个符号序列编码为 [0,1) 区间的一个小数,编码效率高于霍夫曼编码(接近信息熵),常用于 JPEG 2000。
- 哈夫曼编码(Huffman Coding):根据符号出现频率构建二叉树,生成变长编码,如文本压缩(.txt 文件)。
(2)字典编码(Dictionary Coding)
- 查找数据中的重复模式,用索引(字典条目)替代重复内容。
- 典型算法:
- LZ77/LZ78:记录重复数据的位置和长度,如 ZIP 压缩格式的基础。
- DEFLATE:结合 LZ77 和霍夫曼编码,用于 PNG 图像、ZIP 文件压缩,压缩比约 2:1~5:1。
(3)预测编码(Prediction Coding)
- 根据相邻像素的相关性预测当前值,仅存储预测误差(如差分脉冲编码 DPCM),适用于无损图像压缩(如 BMP 转 PNG)。
3. 应用场景
- 需要完全还原的数据:
- 文本文件(.txt、.pdf)、程序代码、压缩包(.zip、.rar)、医学影像(如 DR、CT 的无损格式)、原始传感器数据(如卫星图像原始采样)。
- 图像格式:PNG(无损位图)、GIF(有限色彩无损)、TIFF(可选无损压缩)。
4. 优缺点
- 优点:100% 还原原始数据,适合对准确性要求极高的场景。
- 缺点:压缩比有限(通常 2:1~10:1),无法处理大量冗余度低的数据(如已压缩的图片再无损压缩效果差)。
三、混合编码(Hybrid Coding)
1. 定义与核心思想
- 定义:结合有损压缩与无损压缩的优势,对数据中不同部分采用不同压缩策略,平衡压缩比与保真度。
- 核心思想:对次要信息用有损压缩提高效率,对关键信息用无损压缩保留细节,适用于既需高压缩比又需部分细节保真的场景。
2. 典型技术与应用
(1)JPEG 2000(图像混合编码)
- 策略:
- 对图像进行小波变换(Wavelet Transform),将数据分为低频(轮廓)和高频(细节)部分。
- 对低频部分采用无损压缩(如算术编码),对高频部分采用有损量化压缩。
- 优势:支持 “感兴趣区域(ROI)” 编码 —— 对 ROI 用无损压缩,其他区域用有损压缩,兼顾压缩比和关键细节(如医学图像中的病灶区域)。
(2)视频编码标准(如 H.264/AVC、H.265/HEVC)
- 混合策略:
- 帧内压缩(Intra Coding):对单帧图像采用类似 JPEG 的有损变换编码(DCT + 量化),减少空间冗余。
- 帧间压缩(Inter Coding):利用相邻帧的时间冗余,仅存储运动矢量和残差(预测误差),残差部分可选择有损或无损编码(如 H.264 的无损模式)。
- 应用:蓝光视频、网络流媒体(如 YouTube、Netflix),压缩比可达 100:1 以上,同时通过参数调整(如 QP 值)控制保真度。
(3)医学图像压缩(如 JPEG-LS、JPEG 2000 无损 + 有损模式)
- 对诊断关键区域(如肿瘤边缘)用无损压缩,背景区域用有损压缩,确保医疗诊断的准确性。
3. 技术优势
- 灵活性:可根据需求调整有损与无损的比例,例如:
- 卫星遥感图像:对地表轮廓用有损压缩,对坐标等元数据用无损压缩。
- 手机相机 RAW 格式:部分厂商采用混合编码,保留色彩信息的同时压缩亮度数据。
- 高性价比:在相同文件大小下,混合编码的图像 / 视频质量通常高于纯有损压缩(如 H.265 比 H.264 在相同码率下质量提升约 50%)。
四、三种压缩方式对比表
| 指标 | 有损压缩 | 无损压缩 | 混合编码 |
|---|---|---|---|
| 信息保留 | 舍弃部分次要信息 | 完全保留原始信息 | 关键信息无损,次要信息有损 |
| 压缩比 | 高(10:1~100:1+) | 中低(2:1~10:1) | 中高(结合两者优势) |
| 可逆性 | 不可逆 | 完全可逆 | 部分可逆(关键信息可逆) |
| 典型算法 | JPEG、MP3、H.264 | 霍夫曼、ZIP、PNG | JPEG 2000、H.265、JPEG-LS |
| 应用场景 | 照片、视频、音乐 | 文档、代码、医学影像 | 遥感图像、医疗影像、4K 视频 |
| 质量风险 | 高压缩比时质量下降 | 无质量损失 | 可控制质量损失范围 |
五、实际应用中的选择策略
- 优先有损压缩:对质量要求不高、存储空间有限的场景(如社交平台图片、在线视频)。
- 优先无损压缩:对数据准确性要求极高的场景(如财务报表、程序安装包)。
- 选择混合编码:
- 需平衡压缩比与关键细节的场景(如医学影像、专业摄影 RAW 文件)。
- 视频编码中,通过帧内 / 帧间混合策略在有限码率下实现高清画质(如 8K 视频传输)。


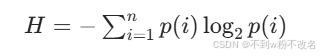

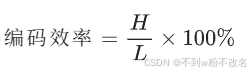













)




】接口)



